Introdução ao R
R é uma linguagem e ambiente para computação estatística e gráficos. É um projeto GNU que é semelhante à linguagem e ambiente S que foi desenvolvido nos Laboratórios Bell (anteriormente AT&T, agora Lucent Technologies) por John Chambers e colegas. R pode ser considerado como uma implementação diferente de S. Existem algumas diferenças importantes, mas muito código escrito para S é executado inalterado em R.
R fornece uma ampla variedade de técnicas estatísticas (modelagem linear e não linear, testes estatísticos clássicos, análise de séries temporais, classificação, agrupamento, …) e gráficas, e é altamente extensível. A linguagem S é frequentemente o veículo de escolha para pesquisa em metodologia estatística, e R fornece uma rota de código aberto para a participação nessa atividade.
Um dos pontos fortes do R é a facilidade com que gráficos de qualidade de publicação bem projetados podem ser produzidos, incluindo símbolos matemáticos e fórmulas quando necessário. Grande cuidado foi tomado com os padrões para as pequenas escolhas de design em gráficos, mas o usuário mantém o controle total.
R está disponível como Software Livre sob os termos da GNU General Public License da Free Software Foundation na forma de código-fonte. Ele compila e roda em uma ampla variedade de plataformas UNIX e sistemas similares (incluindo FreeBSD e Linux), Windows e MacOS.
O ambiente R
R é um conjunto integrado de recursos de software para manipulação de dados, cálculo e exibição gráfica. Inclui
- uma instalação eficaz de manipulação e armazenamento de dados,
- um conjunto de operadores para cálculos em matrizes, em particular matrizes,
- uma coleção grande, coerente e integrada de ferramentas intermediárias para análise de dados,
- facilidades gráficas para análise de dados e exibição na tela ou em cópia impressa, e
- uma linguagem de programação bem desenvolvida, simples e eficaz que inclui condicionais, loops, funções recursivas definidas pelo usuário e recursos de entrada e saída.
O termo “ambiente” pretende caracterizá-lo como um sistema totalmente planejado e coerente, em vez de um acréscimo incremental de ferramentas muito específicas e inflexíveis, como é frequentemente o caso de outros softwares de análise de dados.
R, como S, é projetado em torno de uma verdadeira linguagem de computador e permite que os usuários adicionem funcionalidades adicionais definindo novas funções. Grande parte do sistema é escrito no dialeto R de S, o que torna mais fácil para os usuários seguirem as escolhas algorítmicas feitas. Para tarefas computacionalmente intensivas, o código C, C++ e Fortran pode ser vinculado e chamado em tempo de execução. Usuários avançados podem escrever código C para manipular objetos R diretamente.
Muitos usuários pensam no R como um sistema de estatísticas. Preferimos pensar nele como um ambiente no qual as técnicas estatísticas são implementadas. R pode ser estendido (facilmente) por meio de pacotes . Existem cerca de oito pacotes fornecidos com a distribuição R e muitos mais estão disponíveis através da família CRAN de sites da Internet, cobrindo uma ampla variedade de estatísticas modernas.
O R possui seu próprio formato de documentação semelhante ao LaTeX, que é usado para fornecer documentação abrangente, tanto on-line em vários formatos quanto em cópia impressa.
Instalação
Instalando o R e o RStudio
Instalar o R é trivial: basta ir no http://cran.r-project.org/ e baixar a versão para o seu computador. Exceto se você usar alguma distribuição de Linux (Ubuntu, por exemplo): ai é mais difícil, mas o próprio CRAN dá instruções de como fazer. Depois, recomenda-se baixar o R Studio, disponível em https://www.rstudio.org/. O R Studio é uma IDE (Integrated Development Enviroment), que facilita muito a vida na hora de programar - especialmente dando sugestões de comandos e mostrando quais variáveis estão salvas no ambiente do R. Assim, sugiro instalar o R Studio, que é bem tranquilo. Para usar o R Studio, você precisa ter o R.
Uma alternativa
Se o seu computador tem um processador multi-core, pode ser interessante instalar o Microsoft R, disponível em http://mran.microsoft.com/. Ele é idêntico ao R, mas vem com uma biblioteca que tira vantagem dos vários núcleos do processador, o que o R padrão não faz. A principal desvantagem é que ele é atualizado com menos frequência, e a biblioteca que usa mais de um núcleo não está disponível para o Mac. Ele funciona com o R Studio.
Interface
A interface do R Studio mostra 4 espaços diferentes: no canto esquerdo superior, existe uma tela chamada source (se ela não estiver lá, tente usar ctrl + shift + n para abrir); a direita dela, o ambiente; no canto inferior esquerdo, está o console; e no canto inferior direito está uma tela multiuso, que deve vir com as abas plot, files. Cada uma dessas será explicada, por alto, nesta seção
A que mais nos interessa, em um primeiro momento, é o console. Nele, você pode passar comandos direto para o R. Digitando 2 + 2 nele e clicando em enter, o resultado deve aparecer na tela. Em geral, é nele que você vai trabalhar. Entretanto, escrever código muito longos no console é muito ruim. O console é desorganizado, não permite salvar o código passado para ele para ser usado mais tarde e não permite com que você corrija erros com facilidade. O source serve justamente para escrever um código longo - uma função ou uma simulação, por exemplo - que pode ser executado no console. Para isso, basta selecionar o conteúdo e dar ctrl + enter ou chegar no fim da linha e usar ctrl + enter.
A tela do canto direito inferior é uma “geleia geral”: a aba plots é onde os gráficos que faremos vão aparecer; a aba files permite você ver arquivos em diferentes pastas do computador. Estas são as abas mais importantes e que mais serão usadas. Em cima desta tela, há a tela environment, que mostra as variáveis que foram criadas e estão disponíveis para o R usar
Erros, Warnings e letras vermelhas
Tão importante quanto saber fazer a coisa certa é saber quando temos um problema. Existem dois tipos de erro:
- Error: esses são de fato erros, e o R não consegue proceder. O que você escreveu tem algum problema grave e não pode ser executado.
- Warning: o R conseguiu fazer o que você pediu, mas alguma coisa esquisita aconteceu, e o R está te avisando.
Veja que em ambos os casos a mensagem vai aparecer em vermelho no console. Error e warnings vem das mais diferentes formas (afinal, é possível errar de diferentes formas). Alguns são claros, como tentar somar um número e uma letra:
2 + "a"## Error in 2 + "a": argumento não-numérico para operador binário(Apesar de operador binário não ser exatamente óbvio)
Outros são mais misteriosos, e quando encontramos um erro impossível de entender, coloque o output do console no google. Typos geram muitos erros (ex.: esquecer o parêntese, errar o nome de um objeto). Em um código longo, descobrir o erro pode ser difícil. Existem ferramentas para isso, e o próprio source do RStudio indica linhas com algum erro com um x vermelho do lado do número da linha. Em geral, em um código muito longo, não é uma estratégia ruim escrever uma parte do código, testar e debugar (retirar os erros) ela. Funções ajudam a fazer isso: trataremos delas mais a frente.
É importante notar que, apesar de uma linha de código que devolva um warning não está errada, ela pode muito bem fazer uma coisa que você não quer. Assim, um warning surpresa deve ser visto com bastante cuidado e normalmente você não deve ignorar um warning.
Veja que essas mensagens não são as únicas que aparecem em vermelho no R: quando o R instala ou carrega um pacote ele exibe algumas coisas em vermelho1. Não se preocupe: isso não quer dizer que o R encontrou algum erro ou warning ao instalar o pacote, é apenas o comportamento padrão do R.
Pacotes
O grande atrativo do R são os pacotes. Para instalar um pacote, basta digitar no console:
install.packages("nome-do-pacote")É necessário colocar as aspas para o pacote instalar. Uma vez instalado, o pacote não é carregado automaticamente. Para carregar o pacote, basta digitar no console:
library(nome-do-pacote)Agora as aspas não são necessárias.
Instalar pacote por pacote pode ser uma tarefa chata. Além do mais, isto exige que você saiba quais são os pacotes que fazem cada coisa. Felizmente, o CRAN mantém coleções de pacotes de determinados temas, chamados de Task Views. Existe um de econometria, e para instalar ele é necessário instalar o pacote ctv , e depois o task view de econometria:
install.packages("ctv")
library(ctv)
install.views("Econometrics")Como são muitos pacotes, esta operação pode tomar algum tempo. Em geral, muitos dos pacotes nos task view não são tão úteis, então pode ser interessante ir no cran, e visitar os task views para selecionar quais pacotes de lá fazem o que você precisa fazer. Existem vários pacotes, para diferentes áreas. Para os economistas, além do pacote de econometria, os pacotes de Time Series, Bayesian, Finance, Machine Learning podem ser de interesse. De fato, com a expansão das áreas de pesquisas, muitos outros task views podem ser de interesse! Recomenda-se visitar o cran para ter uma visão do que está disponível.
| Hands on! |
|---|
Vamos instalar um primeiro pacote que adiciona vários comandos importantes para econometria e alguns datasets de livros de econometria (como o Stock Watson). O nome do pacote é AER. Ele vai instalar vários outros pacotes que ele necessita para funcionar, então a instalação pode demorar um pouco. Ele será usado de agora por diante, então tenham certeza que ele está carregado, ou seja, que vocês sempre estão usando o library(AER) quando abrem o R. |
Ajuda
Em 90% do tempo você vai precisar de olhar o help: seja para lembrar que opções estão disponíveis em um comando, ou lembrar exatamente o que o comando faz, ou descobrir qual o comando para fazer alguma coisa específica que você só tem uma palavra chave: Como gera números saídos de uma distribuição normal mesmo?’’2
Se você sabe o comando e quer ler o help deste comando, basta fazer ?comando. Por exemplo, se você quiser saber o que o comando rnorm faz e quais as opções ele oferece, basta digitar no console ?rnorm. Se você não sabe o nome do comando, mas quer saber todos os comandos que estão relacionados a uma determinada palavra chave, use ??palavra. Por exemplo, se você quiser saber todos os comandos que envolvem a distribuição normal, basta usar ??normal. Observe que, se você tiver muitos pacotes, isto pode demorar um pouco, já que exige que o R procure cada pacote que se referencie àquela palavra.
Você também pode estar interessado em todos os comandos de um pacote. Neste caso, a melhor solução é é usar help(package=``nome-do-pacote'').
Comentando
Em geral, quando se escreve um código, é importante explicar o que algumas partes do código fazem. Isso não é exclusivo para o caso em que o código vai ser distribuído: pelo contrário, o você do futuro vai agradecer muito o você do passado se você comentar o seu código. Para comentar o código no R, usa-se o #. Tudo depois do # vira um comentário é ignorado pelo R. Assim, suponha que queremos explicar o que o parâmetro a abaixo é: suponha que ele vem de um outro estudo, de Cleese et. al. (1975). Então:
a <- 1 #Retirado de Cleese et. al. (1975)A regra geral para comentários é: eles não devem ser óbvios (ex.: 1 + 1 # somando dois números) mas devem ajudar o leitor - que eventualmente será você mesmo - a entender o que está sendo feito - especialmente em momentos mais obscuros.
Objetos*
Como muitas linguagens de programação, existem vários tipos de objetos no R. Objetos são maneiras diferentes de guardar os dados. Os mais usados e mais comuns são:
- Vetor
- Matriz
- Dataframe
- Lista
Em geral, para dar um nome a um objeto, usamos uma setinha, <-, que é o sinal de menor e o menos. Podemos usar o igual também, mas é preferível a seta. Então, se fizermos a <- 1 e digitarmos a, o R vai mostrar 1. Veja que por padrão o R não mostra o valor de objetos que você acabou de criar, e vai mostrar apenas se você pedir.
a <- 1
a## [1] 1Vetores são só coleções unidimensionais de “coisas”. Para criar um vetor, basta usar c() e separar os elementos por vírgula. Suponha que queremos listar os 4 primeiros números primos, então poderíamos fazer:
primos <- c(2,3,5,7)Assim, ao digitar no console primos:
primos## [1] 2 3 5 7Podemos fazer operações com vetores, como somar, subtrair, multiplicar e dividir. Observe que multiplicar um vetor não é multiplicar uma matriz: o R vai multiplicar elemento a elemento. Então c(1,2,3)*c(1,2,3) gera como resultado:
c(1,2,3)*c(1,2,3)## [1] 1 4 9Para multiplicar dois vetores como multiplicariamos usualmente, usamos %*%:
c(1,2,3)%*%c(1,2,3)## [,1]
## [1,] 14Podemos agrupar vetores em matrizes, usando os comandos cbind e rbind, que transforma cada vetor em uma coluna ou em uma linha, respectivamente. Assim, se fizermos cbind(c(1,2),c(3,4)), teríamos:
cbind(c(1,2),c(3,4))## [,1] [,2]
## [1,] 1 3
## [2,] 2 4Se usarmos o rbind(c(1,2),c(3,4)), teríamos:
rbind(c(1,2),c(3,4))## [,1] [,2]
## [1,] 1 2
## [2,] 3 4Existe outra maneira de fazer matrizes, com o comando matrix. Veja que as operações *e %*% funcionam assim como elas funcionam com vetores: *multiplica elemento a elemento a matriz e %*%multiplica a matriz da maneira usual:
A <- matrix(c(1,2,3,4),ncol = 2)
B <- matrix(c(1,1,1,1),ncol = 2)
A*B## [,1] [,2]
## [1,] 1 3
## [2,] 2 4A%*%B## [,1] [,2]
## [1,] 4 4
## [2,] 6 6Observe que matrizes forçam todos os elementos a serem do mesmo tipo. Suponha que você quer fazer uma matriz com nomes e notas de alunos, e quer tirar a média das notas. O R vai acusar um erro, porque as notas não serão do tipo numérico, e sim do tipo character, que é o tipo do nome dos alunos. Para contornar este problema e poder agregar vetores com diferentes tipos - como é o caso do exemplo de notas de alunos e notas é que existe o objeto do tipo dataframe. O comando data.frame funciona como um cbind, que permite diferente juntar vetores de diferentes tipos em uma “matriz”.
Observe que, para formar matrizes e dataframes, os vetores tem que ter o mesmo tamanho, o que nem sempre é possível ou desejável. Neste contexto, existem as listas, que são um anything goes. Você pode ter uma lista de vetores, uma lista de variáveis, uma lista de listas etc. Além disto, você pode dar nomes as coisas dentro dela e chamar pelo nome. Por exemplo, se fizermos:
um.teste <- list(Ola = "Olá", Dia = date())E depois digitarmos um.teste$Dia, ele deve exibir qual a data atual. Digite um.teste$Ola e ele deve exibir um Olá na sua tela:
um.teste$Dia## [1] "Fri May 1 11:40:31 2020"um.teste$Ola## [1] "Olá"Observem que eu usei um “Olá”, entre aspas na lista. Aspas são bastante importante. Por exemplo, faça: c("Bom","Dia"). O R vai mostrar na tela as duas palavras. Agora, suponha que você esquecesse as aspas no Dia. Agora, o R dará um erro: ele afirma que o objeto Dia não foi encontrado.
Assim, se quisermos digitar palavras, frases, letras, devemos colocar eles entre aspas. Caso contrário, o R vai buscar o objeto com aquele nome. De maneira bastante grosseira, expressões desse tipo são chamadas de string.
Familiarizados com como instalar, pedir ajuda, e os principais objetos do R, podemos proceder para a primeira etapa de qualquer análise de dados: como inserir os dados no R.
O coração de econometria é o modelo de regressão linear, estimado por Mínimos Quadrados Ordinários. Mas muitos outros métodos são úteis, como modelos logit, probit, variáveis instrumentais e modelos para painel. Este capítulo trata - finalmente! - de modelos de regressão no R.
##Mínimos quadrados ordinários
Suponha que carregamos uma base de dados (chamada dados), e que esta base tem as variáveis y,x.1,x.2,x.13y,x.1,x.2,x.13 e que nosso objetivo é estimar um modelo da forma: y=β0+β1x1+β2x2+β3x3+ϵy=β0+β1x1+β2x2+β3x3+ϵ. O comando que faz estimativa por mínimos quadrados é o lm e para estimarmos a regressão proposta basta fazer:
reg <- lm(y ~ x.1 + x.2 + x.3 + x.4, data = dados)Usamos o ~ para separar a variável explicada (à esquerda do til) das explicativas (à direita do til), e para separar as explicativas usamos o +. A opção data diz ao R onde buscar as variáveis.
Agora, o objeto reg5 tem o modelo estimado. Para obter uma tabela usual de regressão, com valor do coeficiente, erro padrão, estatística t e p-valor, R2R2 ajustado, e o teste F para os coeficientes basta usar summary(reg). No contexto de regressão linear, podemos querer fazer uma série de coisas, que são explicadas a seguir.
Atenção: Séries Temporais e o lm Objetos de série temporal são armazenados pelo R de uma maneira especial - uma vez que você transforma ele em um objeto de série temporal. Entretanto, você não deve passar um objeto de série temporal para o lm(), já que o lm vai ignorar o formato de série temporal. Assim, estimar um modelo AR(1) usando lm(y ~ lag(y)) vai gerar uma regressão com coeficiente 1 para lag(y) e R2=1R2=1. De fato, a regressão feita foi y em y - o que não é uma regressão muito emocionante.
Testes de hipótese
Suponha que queremos testar a significância conjunta de x.2 e x.3. Precisamos fazer um teste F. Uma maneira é estimar um novo modelo, que chamaremos de reg.2, só com o x.1: reg.2 <- lm(y ~ x.1)
Agora, para testar a significância conjunta de x.2 e x.3 basta fazer anova(reg,reg.2) e o R reportará os valores do teste (incluindo o p valor)
Testes mais gerais também estão disponíveis, pelo pacote car6. O comando é linearHypotesis com o primeiro argumento sendo o objeto com o modelo. O segundo comando é a hipótese que estamos testando, entre aspas, e entramos ele de maneira extremamente intuitiva: suponha que no exemplo acima queremos testar se o coeficiente de x.2 é igual ao coeficiente de x.4. Nesse caso, o comando se resumiria a linearHypotesis(reg,"x.2 = x.4"). Várias opções podem ser usadas, como usar estimadores de erro padrão robustos a heterocedasticidade. Recomendamos que o leitor olhe o help do comando no R.
Erros padrões robustos
Na presença de heterocedasticidade ou autocorrelação, os erros padrões usuais não são confiáveis. Infelizmente, o comando summary não exibe erros robustos por default e nem permite alterar os erros padrões exibidos. Felizmente, o pacote lmtest traz uma opção para o sumário padrão do R. A primeira coisa a fazer é carregar o pacote sandwich (library(sandwich)). O comando é coeftest e a sintaxe é curiosa. No caso do nosso exemplo, se quisermos obter erros robustos a heterocedasticidade:
coeftest(reg, vcov. = vcovHC(reg))Uma explicação: O comando coeftest chama o comando vcovHC do pacote sandwich. Por sua vez, o comando vcovHC precisa saber qual o modelo que vai ter erros robustos. Por isso uma função que recebe uma função. Veja que se quisermos erros robustos a heterocedasticidade e autocorrelação, o comando vira vcovHAC.
Logs
Muitas vezes queremos fazer as regressões não com as variáveis em nível, mas com as variáveis em log. Nesse caso, suponha que queremos a variável dependente - y - em log. Para isso, basta fazer log.y <- log(y) e a variável log.y vai ser a versão em log da variável y. Você pode reescrever a regressão como lm(log.y ~ x.1 + x.2 + x.3).
Agora, pode ocorrer de em alguns casos o vetor y ter algum elemento zero. Mas log(0)=−∞log(0)=−∞. O R tem um elemento Inf (e - Inf) para esses casos, mas o comando lm vai acusar um erro ao receber um vetor com algum elemento Inf. A solução é trocar esse valor para alguma coisa, como um NA, que o R vai ignorar7. Para fazer isso, suponha que o vetor com os Inf seja o log.y do paragrafo anterior. Precisamos explicar para o R quais casos nós queremos substituir, e isso é incrivelmente fácil: assim como podemos usar log.y[1] para escolher o primeiro elemento do vetor log.y, podemos colocar entre colchetes uma condição, por exemplo os elementos do vetor log.y que são iguais a infinito. Já tratamos disso: log.y == -Inf faz esse trabalho. Assim, se quisermos substituir os elementos de log.y que são iguais a -Inf por NA, basta usar o seguinte trecho de código:
log.y[log.y == -Inf] <- NAProbits e Logits
Probits e logits também são úteis quando nossa variável dependente é uma dummy. Sempre podemos usar um modelo de probabilidade linear, e nesse caso o comando a ser utilizado é o lm. Mas em casos que queremos usar um probit ou logit, precisamos recorrer ao glm, que tem sintaxe muito parecida com o lm. Mas além de especificar as variáveis dependentes e independentes, também precisamos especificar o tipo de regressão, basicamente a distribuição da variável dependente. No caso de probits e logits, a variável dependente tem distribuição binomial. Depois, temos que especificar se a função de probabilidade da variável dependente é probit ou logit. Os comandos para estimar probits e logits são ilustrados abaixo:
mod.1 <- glm(y ~x.1 + x.2 + x.3, family = binomial(link = 'probit'))
mod.2 <- glm(y ~x.1 + x.2 + x.3, family = binomial(link = 'logit'))E como de praxe, podemos usar o comando summary para obter os coeficientes, desvios padrões e estatísticas t.
Variável instrumental
Métodos de variável instrumental são muito úteis e populares, especialmente em casos de endogenidade. Existem várias implementações, mas para o mínimos quadrados de dois estágios usual, o pacote AER oferece um comando ivreg. A sintaxe é similar ao lm, mas com uma alteração na formula para inserir os instrumentos, que são separados dos regressores por |.
Por exemplo, suponha que temos a variável dependente y, as variáveis endogenas x.1 e x.2, a variável exogena x.3, e os instrumentos z.1 e z.2. Nesse caso, o ivreg seria usado:
modelo <- ivreg(y ~x.1 + x.2 + x.3|z.1+z.2+x.3)E podemos usar o summary para ver o valor dos coeficientes, erros padrão e estatísticas t. Observe que o pacote não mostra o valor do teste F para o primeiro estágio nem de teste de sobre identificação.
Dados em painel
Em muitas aplicações usamos dados em painel - i.e., com dimensão temporal e cross section. Em geral, esse tipo de aplicação acaba envolvendo o uso de efeitos fixos. Existem duas maneiras de fazer: usando o pacote plm ou “na mão”, usando o lm. Não há nenhuma vantagem de usar o lm “na mão”, em geral, exceto em casos que temos mais de duas dimensões ou por algum motivo o plm não funciona. Exploraremos primeiro o uso do plm, que deve satisfazer a maioria dos usuários. A solução na mão vem depois e pode ser ignorada sem perda de continuidade.
Supondo que o pacote já foi instalado e carregado, precisamos (i) explicar para o pacote quais colunas são as colunas com efeitos fixos de tempo e unidade e (ii) rodar a regressão propriamente dita. Suponha, como de praxe, que temos um dataframe carregado no R com nome “dados”. Suponha que as colunas com as datas e um índice para unidades se chamam datas e unidades, respectivamente. Veja que essas colunas podem estar em formato de carácter, e que isso não deve nos preocupar no momento: poderia ser o caso de a unidade ser estados do país e o código da unidade ser o código do estado (DF,RJ,SP,…). O pacote plm disponibiliza o comando plm.data, que converte um data frame de forma que quando rodarmos a regressão, o R saiba quem são os efeitos fixos. Assim, vamos criar um dataframe chamado dd:
dd <- plm.data(dados,c('unidades','datas'))O primeiro argumento da função é o data.frame a ser convertido, que contém as colunas para as quais criaremos efeitos fixos. O segundo argumento da função são as colunas com os efeitos fixos. Veja que a ordem é unidade e depois a variável temporal. Agora, a estimação do modelo pode ser feita usando o comando plm, que tem sintaxe muito similar ao lm: passamos uma formula com a variável dependente e as independentes, informamos a base de dados - que nesse caso é o objeto dd, não o objeto dados. Mas temos algumas novas opções: o método de estimação (em geral estamos interessados em within, o padrão), mas mais relevante é que efeitos fixos queremos colocar: só para indivíduo, só para tempo ou ambos. Abaixo, mostramos a sintaxe para cada um dos casos, respectivamente:
mod.1 <- plm(y ~x.1 + x.2,data = dd, effect = 'individual')
mod.2 <- plm(y ~x.1 + x.2,data = dd, effect = 'time')
mod.3 <- plm(y ~x.1 + x.2,data = dd, effect = 'twoways')Como de praxe, podemos usar o comando summary para obter um sumário da regressão.
Painel usando lm*
Suponha que não conseguimos usar o plm por alguma razão. Por exemplo, podemos querer três efeitos fixos: se tivermos microdados de escola, podemos querer ter efeito fixo de aluno, escola e tempo. Podemos implementar isso no braço usando o lm. Lembre-se que, no fundo, efeitos fixos são mera dummies, então se fizermos um modelo linear com dummies, devemos obter resultados parecidos.
Para ficarmos em terreno conhecido, suponha que só temos dois efeitos fixos que nos interessam: unidade e tempo. Cada um desses vem codificado em duas colunas: uma com a data e outra com algum código para a unidade. Lembrem-se da discussão no capítulo anterior que o lm é capaz de usar isso e entender como dummies, sem a necessidade de criar várias variáveis com 0 e 1. Logo, se queremos explicar y usando x como variável explicativa e efeitos fixos de unidade e tempo, a seguinte regressão deve bastar:
modelo <- lm(y ~x +tempo + unidade, data = dados)E y,x,tempo e unidade estão no dataframe chamado dados, como de praxe. Algumas diferenças devem ser notadas para o comando plm:
- O sumário vai ser mais confuso no caso do
lm: oplmesconde os efeitos fixos, o que não ocorre no caso dolm
Mas mais importante:
- Devido a maneira como o
plmestima o modelo (por within, em geral), oplmusa menos graus de liberdade e pode fazer estimações mais precisas. Isso deve impactar mais nos desvios padrões que no valor dos coeficientes, especialmente quando o número de variáveis for muito grande.
Só podemos fazer análise de dados se tivermos… dados. Este capítulo ensina a colocar os dados no R e a manipular eles como para criar variáveis necessárias ou limpar os dados antes de iniciarmos a análise.
Esse capítulo não tenta ser enciclopédico nem detalhista: pelo contrário, ele omite muitas coisas. A omissão mais grave é, sem dúvida alguma, os pacotes do Tidyverse. A omissão se deve a ignorância do autor em usar estes pacotes.
Arquivos excel/csv
O R não lê diretamente arquivos excel (.xls ou .xlsx), apesar de alguns pacotes permitirem o R ler estes arquivos. Mas esta não é a melhor opção: o ideal é salvar a planilha com os dados em outro formato, como .csv. Isto não é difícil: basta, no excel, ir em salvar como, e embaixo na opção de nome do arquivo há a opção de escolher o formato. O que queremos é csv (separado por vírgula)
Para carregar o arquivo no R, precisamos saber algumas poucas coisas:
- O seu excel usa ponto ou vírgula como separador decimal? *Aonde está o arquivo
O item 1 importa porque, se o separador decimal for vírgula, usamos o comando read.csv2. Caso contrário, usamos read.csv. O comando é bem simples: basta passar o caminho (aquele C:/Usuário/…). Por exemplo, suponha que eu tenho um csv chamado dados, e quero importar ele para o R. Ele fica no C:/Usuário/Autor/Manual. Então, eu faria:
read.csv2("C:/Usuário/Autor/Manual/dados.csv")Observe que o caminho para o arquivo está entre aspas e que você precisa colocar a extensão do arquivo no fim - o .csv. Mais uma observação: em geral, se você copiar e colar o caminho como o Windows dá o nome de arquivo com ao invés de /. O R só lê usando /, então você tem que alterar isto.
Neste caso, o R só vai exibir os dados, e não vai salvar eles dentro do R. Você não vai poder fazer nada com os dados. Para podermos usar eles mais tarde, precisamos salvar ele no ambiente do R. Para isto, basta criar um objeto com os dados, como já fizemos no capítulo anterior. Por exemplo, podemos ser extremamente criativos e chamar o objeto de dados. Nesse caso:
dados <- read.csv2("C:/Usuário/Autor/Manual/dados.csv")Se você não está familiarizado com usar o caminho dos arquivos, isto pode parecer excessivamente complicado. Felizmente, o R permite com que você escolha o caminho do arquivo de maneira mais usual, usando um menu e o mouse. Para isto, precisamos alterar o comando acima ligeiramente:
dados <- read.csv2(file.choose())Isto vai abrir o menu e permitir que você escolha o arquivo como um menu do word. Entretanto, apesar de ser mais fácil, essa solução pode ser extremamente inconveniente: toda vez que você for rodar o programa você vai ter que escolher. Apesar de trabalhar com o caminho ser um pouco mais chato, isto poupa muito tempo.
Lendo arquivos do stata e outros pacotes estatísticos
Muitos arquivos com dados ainda são distribuídos em versão de programas estatísticos, como o stata. É fácil ler estes arquivos usando o pacote foreign. Normalmente este pacote já vem instalado, mas caso você não tenha, você pode instalar como qualquer outro pacote. Ele permite ler dados do SAS, SPSS, entre outros. A ideia é a mesma da seção anterior, mas com comandos diferentes para cada tipo de arquivo: o ideal é consultar o help do pacote.
Por exemplo, para ler um arquivo do stata, o comando no pacote foreign é read.dta. Suponha que, ao invés de ser um arquivo .csv, meus dados do exemplo anterior estivessem salvos em formato do stata. Bastaria fazer:
dados <- read.dta("C:/Usuário/Autor/Manual/dados.dta")Porém, o read.dta só lê arquivos criados pelo stata até a versão 12. Para versões posteriores do stata, existe um pacote chamado readstata13. Se, ao usar o read.dta você receber uma mensagem de erro, vale a pena checar o readstata13.
Lendo arquivos muito grandes
Algumas bases de dados podem ser muito grandes, e o R pode sofrer para abrir - mesmo em computadores com muita memória e muito processamento. Para driblar o problema, o pacote data.table ajuda a carregar arquivos grandes para o R. O pacote trás várias opções para trabalhar com os dados carregados, que não serão tratadas aqui.
Outra opção é o pacote readr, que funciona de forma parecida com o comando padrão do R. Para ler um csv que usa vírgulas para separar decimais, o comando é read\_csv2 - basicamente idêntico ao comando padrão do R, mas com uma linha no lugar do ponto. Ao carregar o arquivo, tudo funciona como o usual. Uma pequena diferença é que o nome das variáveis é preservado: assim, uma variável chamada “Nome da variável” continuará se chamando “Nome da variável”, ao invés do padrão do read.csv2 de transformar em “Nome.da.variável”. Apesar de isso parecer bom a primeira vista, dificulta acessar as variáveis mais tarde, já que o R não entende nomes com espaço para objetos.
O pacote BETS (e muitos outros)
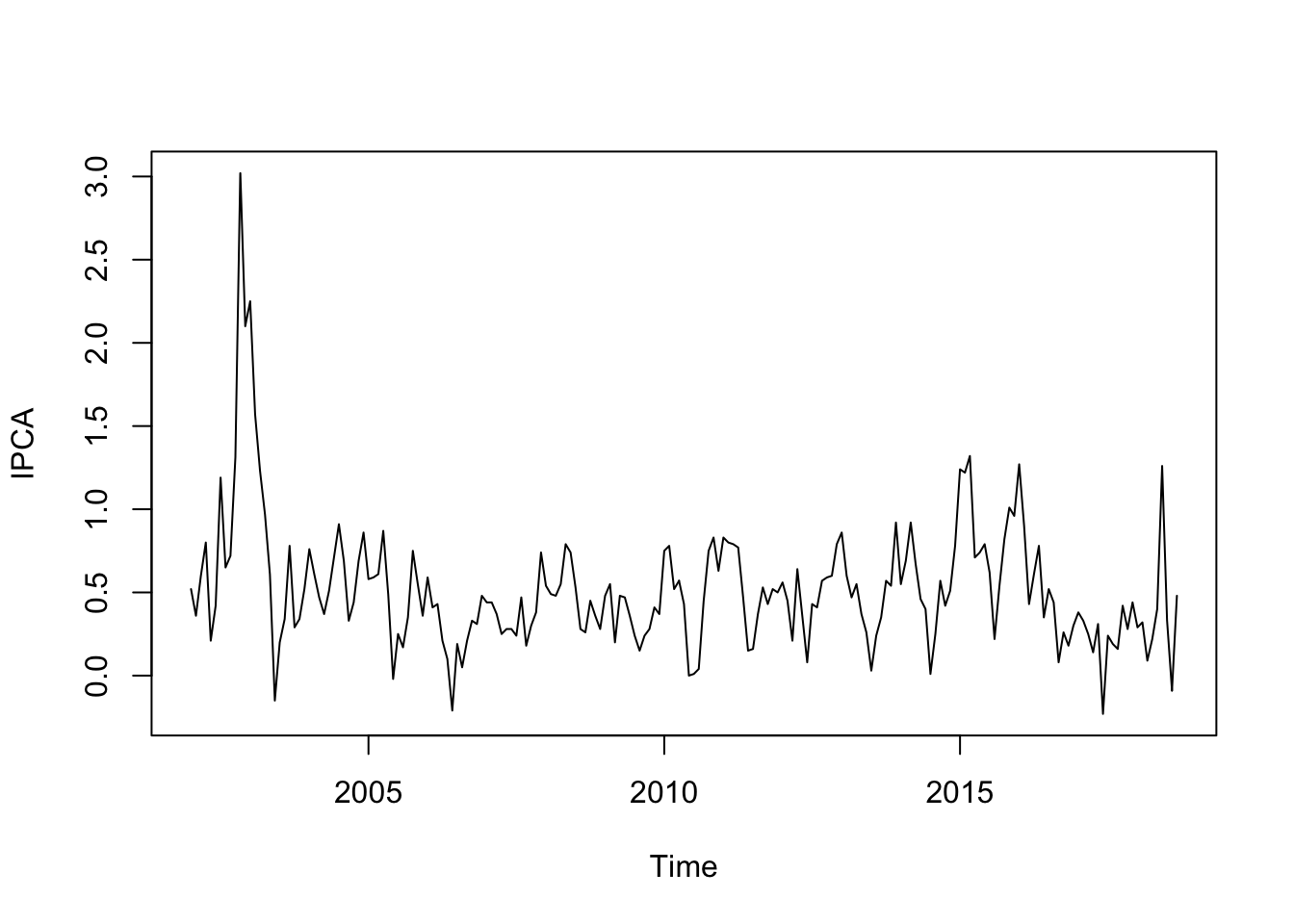
Para dados do Brasil, especialmente dados macroeconômicos, o pacote BETS é uma excelente alternativa para puxar os dados via BCB/IBGE. O BETS permite com que, direto do R, você busque e salve séries disponíveis em diversas bases de dados - entre elas o BCB e o IBGE. O cerne do BETS são os comandos BETSsearch() e BETSget(). O BETSsearch() permite buscarmos por uma palavra chave e retorna informações da série - frequência, fonte, início e fim e um código. O BETSget() permite com que você recupere a série a partir do código. Para recuperarmos o IPCA, fariamos:
library(BETS)
busca <- BETSsearch("IPCA")##
## BETS-package: Found 51 out of 18706 time series.#View(busca)
IPCA <- BETSget(433, from = "2002-01-01")
plot(IPCA)Veja que colocamos o View(busca) comentado apenas para este post: ao rodar essa linha, uma aba no RStudio abrirá e mostrará todas as séries que se encaixam neste critério.
Veja que este não é o único pacote disponível para baixar dados! Existem muitos outros, e a melhor maneira é fuçar o CRAN. (Mas em breve devo adicionar mais um aqui, o Quandl)
Trabalhando com os dados
Uma vez carregado os dados, pode ser necessário manipular os dados de diversas maneiras. Esta seção tratará de algumas das maneiras mais comuns.
Selecionando linhas/colunas/elementos
Selecionar uma linha ou uma coluna específica de uma base de dados é essencial. Se quisermos rodar uma regressão e cada coluna da tabela é uma variável, então temos que ser capazes de informar ao R quais colunas serão usadas como variável explicada e quais como variável explicativa. O R usa a notação de matrizes com colchetes, então para selecionar a 4ª linha da base de dados chamada dados, basta fazer dados[4,]. Veja que colocamos a vírgula e depois deixamos em branco, informando ao R que queremos todas as colunas. Para obter todas as linhas da quarta coluna, fazemos dados[,4].
E se quisermos apenas algumas linhas ou algumas colunas? Podemos passar um vetor dizendo quais são essas linhas e/ou colunas. Por exemplo, se quisermos as linhas 1 a 4, podemos passar um dados[1:4,]. E se quisermos as linhas 1 e 4, podemos fazer: dados[c(1,4),]
Outra maneira, bastante útil, de selecionar variáveis é pelo nome delas. Suponha que os dados vem com nomes id, renda, escolaridade. Para selecionar a variável renda, basta fazer dados$renda. Veja que isso exige saber como (e se) o R importou os nomes. Para isso, a função names permite saber quais os nomes das variáveis. Logo names(dados) vai retornar os nomes das variáveis. Em geral, os espaços são substituídos por pontos, logo uma variável anos de estudo se tornará anos.de.estudo. Veja que também podemos acessar as variáveis em um data.frame usando nome do data.frame$nome da variável. Assim, se temos um data.frame com nome dados e queremos acessar a variável renda, bastaria fazer dados$renda.
Veja que podemos querer selecionar apenas um elemento. No caso de vetor, é a única coisa que faz sentido: o vetor só tem uma dimensão (uma linha ou uma coluna), então só podemos pegar um elemento dele. Suponha que temos o vetor vv e queremos o décimo elemento: basta fazer v[10]. Veja que não usamos vírgulas, que são usadas apenas para separar as dimensões. Se quisermos um elemento de uma matriz, basta passar a linha e a coluna dele, respectivamente. Por exemplo, o elemento da segunda linha e quinta coluna do dataframe dados é obtido usando dados[2,5].
Mas o R permite você selecionar o elemento de uma matriz como se fosse um vetor! Suponha uma matriz - chamaremos ela de MM - com 5 linha e 5 colunas. O último elemento da matriz pode ser obtido com M[5,5] ou, equivalentemente, M[25]. Veja que o 25 não é a toa, no total a matriz tem 25 elementos: logo, o último tem que ser o membro 25.
As vezes, queremos transformar uma variável contínua em uma dummy. Pode ser o caso que queremos isolar apenas aqueles que recebem menos de um salário mínimo, e queremos que quem tiver menos de um salário mínimo tenha valor 1 e, caso contrário, 0. Suponha que o salário mínimo seja 678, e que a variável de salários se chame w. Então, bastaria fazer:
sal.min <- w < 678Observe que o R vai gerar um vetor de Verdadeiros e Falso. É possível converter para numérico, mas não há nenhuma necessidade, uma vez que o R é capaz de interpretar o verdadeiro ou falso como uma dummy na regressão.
O que estamos fazendo é apenas uma operação de compara cada número do vetor ao número 678. Testamos se ele é menor (<), mas poderíamos ver que números são maiores (>), iguais (==)3, menor ou igual (<=) ou maior ou igual (>=). Estes operadores não são apenas úteis para criar dummies, mas também pode servir para escrever funções, que será tratado mais a frente.
Pode ocorrer de a variável vir como um vetor de palavras ou siglas. Suponha que estamos trabalhando com um painel que tem variação temporal e por estado, e o vetor de estados vem com as siglas dos estados (RJ,SP,ES,MG,DF…). Se quisermos usar efeitos fixos de uma maneira extremamente ingênua, poderíamos criar dummies para cada estado e estimar o efeito fixo de cada estado. Esta não é uma maneira inteligente de fazer, já que existem pacotes para fazer estimação usando efeitos fixos com bem menos trabalho, que serão tratados no próximo capítulo. Mas, no momento, vamos ignorar esta opção e tentar criar uma dummy para cada estado.
Uma possível solução era criar um vetor para cada estado (Ou talvez uma matriz com n linha e o número de colunas sendo igual o número de estados), ler cada posição do vetor das siglas usando um loop e colocar um 1 na coluna correspondente, criando um vetor índice para o R buscar qual coluna é relacionada com cada estado… Se a explicação anterior bagunçou o seu cérebro, não se preocupe: ela é complicada, e o R não exige nada tão complicado4
Uma solução muito mais simples é usar o comando factors, que gera automaticamente dummies para cada categoria. Assim, RJ vira uma dummy, SP outra etc. Isso é automático, e podemos jogar direto numa regressão. Assim, suponha que temos uma base de dados chama dados e a coluna 2 é a coluna com os estados. Nesse caso: estados <- factor(dados[,2]). Poderíamos usar estados diretamente na regressão, que será tratada no capítulo seguinte.
Uma nota: a partir da versão 4.0 do R, o comportamento ao importar um arquivo tipo csv mudou. Antes, colunas de caracteres eram automaticamente convertidas em fatores. Agora, as colunas de caracteres permanemce sendo caracteres. Você pode mudar isso coloca no read.csv stringAsFctors = T. Você pode mudar na mão também. Isso é extremamente inconveniente se o seu plano é fazer uma regressão linear, mas extremamente conveniente pra outra parte dos usuários.
Métodos de séries temporais são suficientemente extensos e únicos para terem seu próprio capítulo. Este capítulo trata dos principais métodos de séries temporais de interesse dos economistas: ARIMAs, VARs, testes de raiz unitária e cointegração. Séries temporais são únicas o suficiente a ponto de terem um classe própria - sem nenhuma surpresa, ela se chama time series.
O básico
Suponha que você, usando os métodos do capítulo 2, inseriu uma série temporal no R. O R não sabe, a priori, que os dados são uma série temporal. Você precisa contar isso a ele, e o comando que faz isso é o ts(). O ts recebe a série, a data de ínicio e a frequência. A frequência é como você dividiu o ano: 4 se o dado for trimestral, 12 se for mensal…
Por exemplo, podemos gerar uma série de variáveis aleatórias da normal (um ruído branco) e transformar em série temporal mensal começando em janeiro de 2000:
serie <- rnorm(1000)
serie <- ts(serie,start =c(2000,01), freq = 12)Veja que o comando ts() é excessivamente engessado: os dados tem que ter uma frequência fixa, expressa como uma fração do ano. O pacote zoo extende bastante as capacidades do R em lidar com séries temporais, inclusive com séries irregulares.
Atenção: Séries Temporais e o lm Você não deve passar um objeto de série temporal para o lm(), já que o lm vai ignorar o formato de série temporal. Assim, estimar um modelo AR(1) usando lm(y ~ lag(y)) vai gerar uma regressão com coeficiente 1 para lag(y) e R2=1R2=1. De fato, a regressão feita foi y em y - o que não é uma regressão muito emocionante.
##ARIMAs
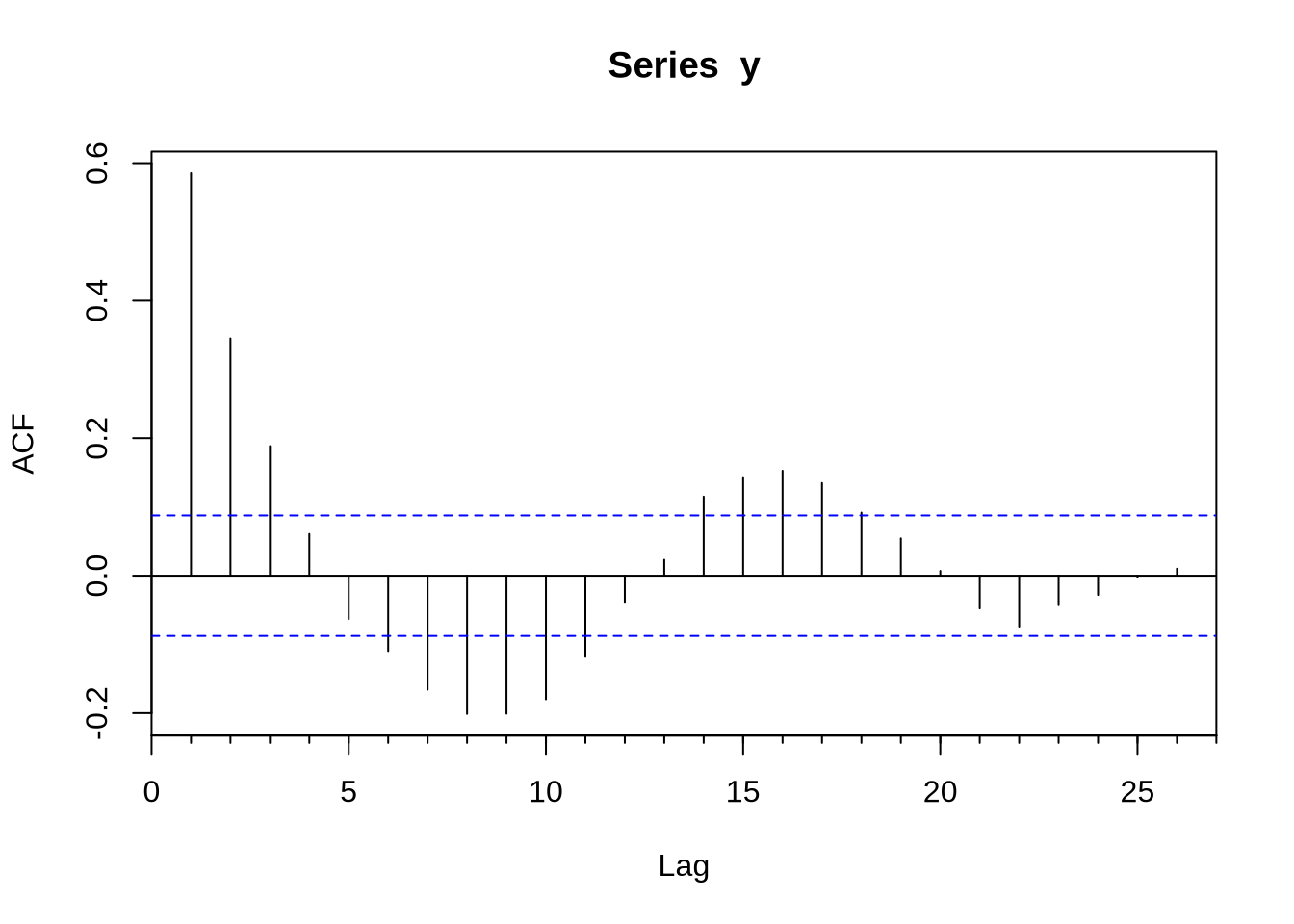
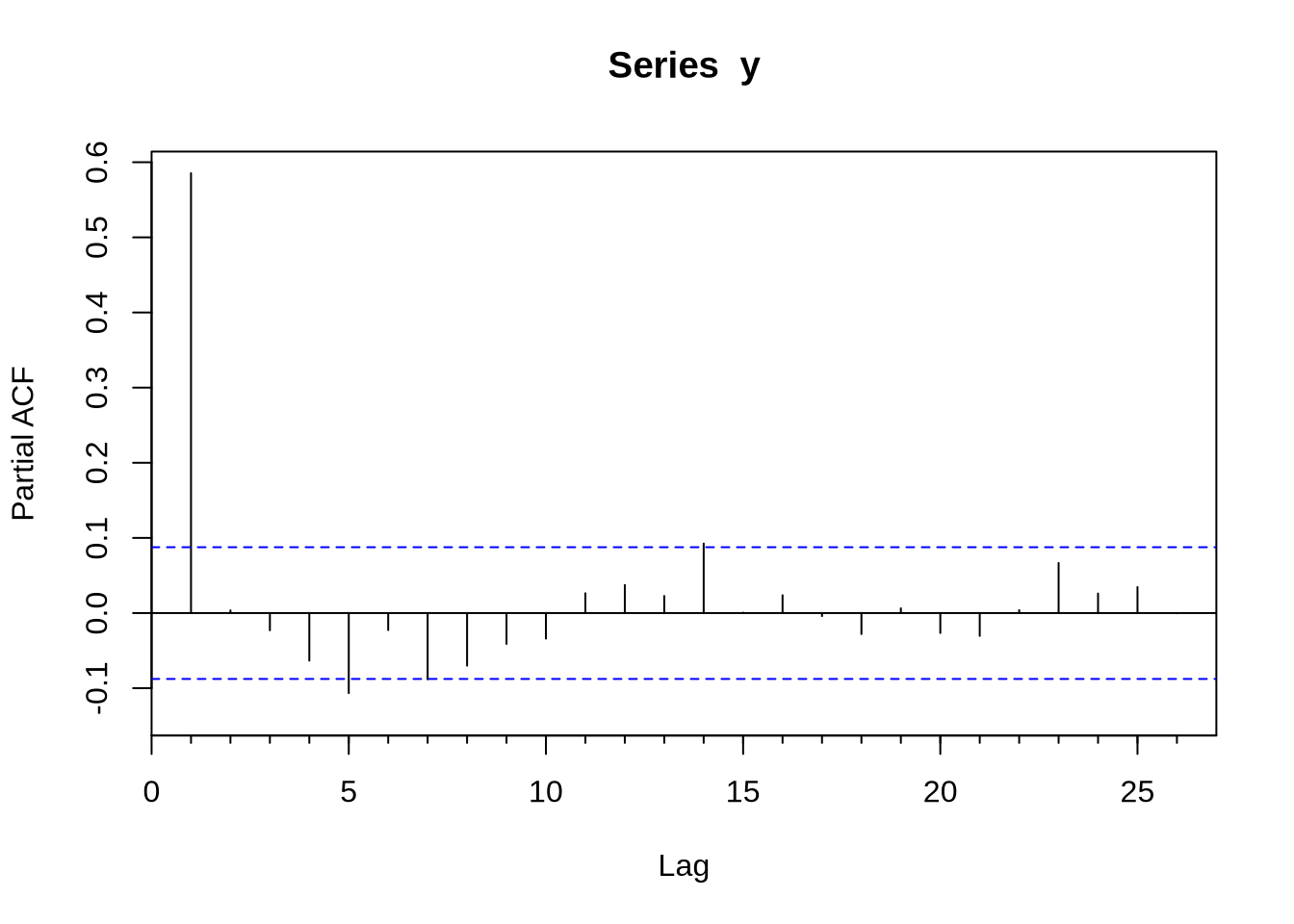
Com uma série devidamente construída para ser um objeto ts - como nós fizemos acima- podemos tentar estimar algum modelo. O modelo base de séries temporais é o ARIMA. O R base já vem com muitas funções para lidar com isso, mas o pacote forecast extende bastante as capacidades do R em lidar com esse tipo de série. O primeiro passo para estimar um modelo Arima é obter a função de autocorrelação (FAC) e a função de autocorrelação parcial (FACP): elas são Acf e Pacf. Veja que existem versões na base do R que se chamam acf e pacf (notem que lá é com maiúscula e aqui com minúscula). A diferença fundamental entre os dois é que a Acf e a acf (e também a Pacf e a pacf) é que a primeira exclui a autocorrelação no momento 0 - que é trivialmente 1.
Uma vez conhecendo o formato da FAC e da FACP, podemos estimar o ARIMA. O comando para estimar um modelo ARIMA é Arima - e novamente, existe um arima com minúscula que é da base do R. O Arima basicamente recebe duas coisas, a série e a ordem do modelo(isso é, se o modelo é um ARMA(1,1), AR(1), MA(1) etc). Vamos gerar um exemplo de um AR(1) com dados simulados e obter a FAC e FACP e estimar o modelo Arma sugerido:
library(forecast)
u <- rnorm(500)
y <- rep(0,500) #nossa futura série
y[1] <- u[1]
for(i in 2:500){
y[i] <- 0.6*y[i-1] + u[i] #um AR(1) com coeficiente 0.6
}
Acf(y)Pacf(y)modelo <- Arima(serie,order=c(1,0,0))
summary(modelo)## Series: serie
## ARIMA(1,0,0) with non-zero mean
##
## Coefficients:
## ar1 mean
## -0.0312 -0.0157
## s.e. 0.0316 0.0315
##
## sigma^2 estimated as 1.06: log likelihood=-1447.14
## AIC=2900.28 AICc=2900.31 BIC=2915
##
## Training set error measures:
## ME RMSE MAE MPE MAPE MASE ACF1
## Training set 1.500234e-05 1.028603 0.8091188 98.585 111.1065 0.7103052 -0.0002764195Veja que o objeto modelo trás os coeficientes estimados, o erro padrão e alguns diagnósticos úteis como critérios de informação.
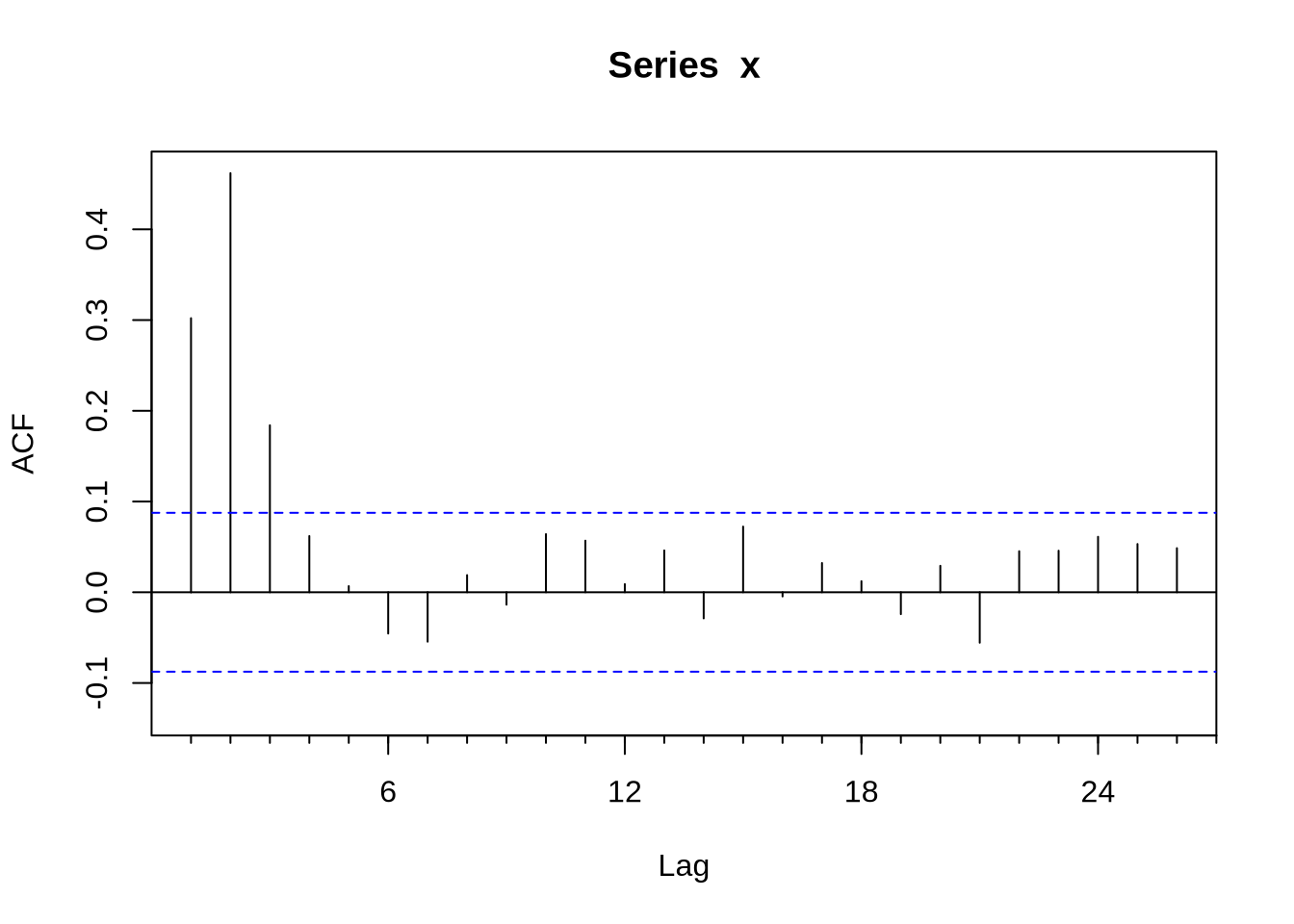
Em algumas situações pode ser muito difícil inferir o modelo certo a partir da FAC e da FACP. O comando auto.arima, do pacote forecast, seleciona um modelo a partir de algum critério de informação. Vamos ilustrar o ponto gerando uma série x que é um ARMA(1,2):
e <- rnorm(1000)
x <- rep(0,1000)
for(j in 1:998){
x[j+2] <- 0.5*x[j+1] + e[j+2] - 0.3*e[j+1] + 0.4*e[j]
}
x <- x[500:1000]
x <- ts(x, start = c(1999,05), freq = 12)
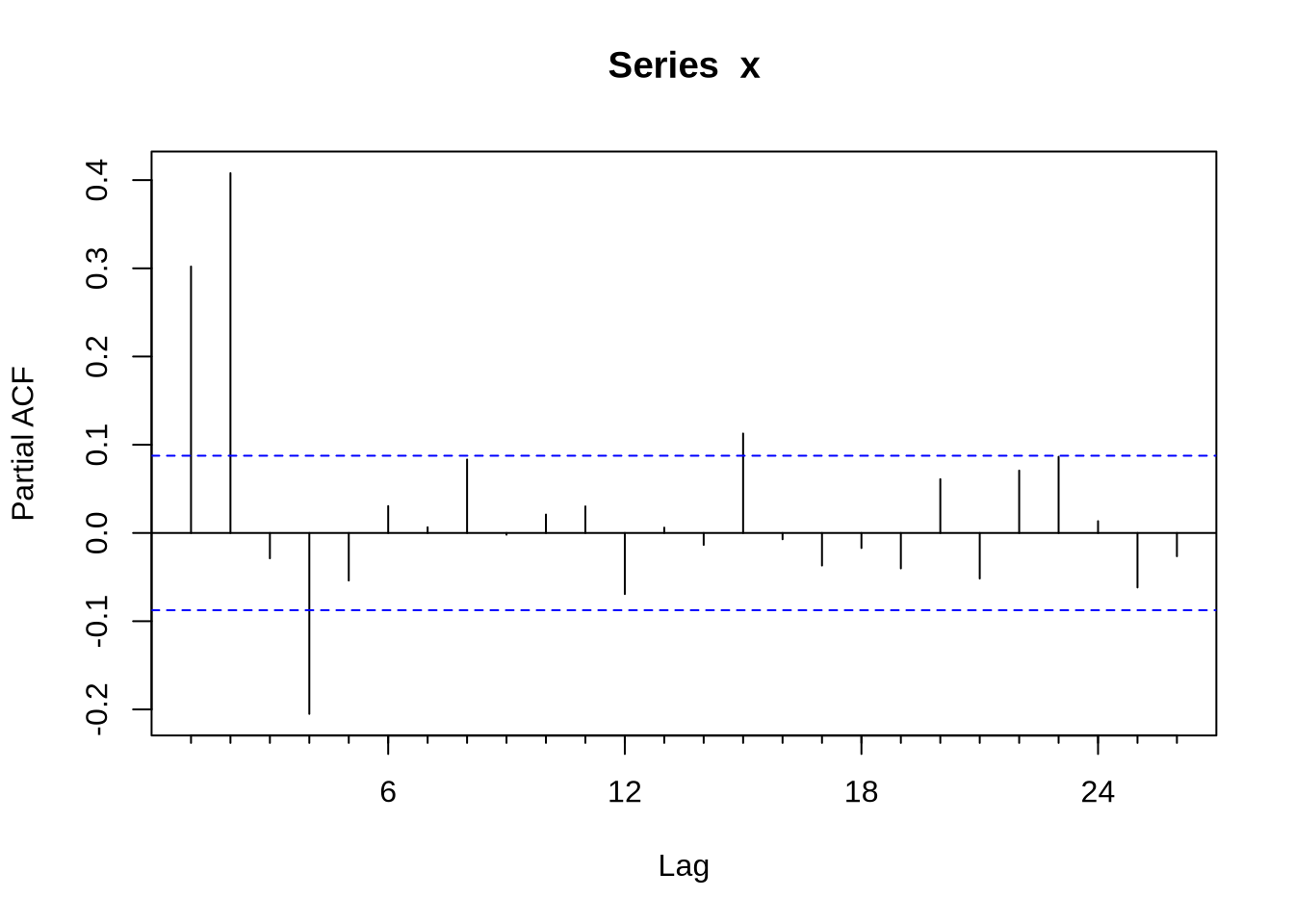
Acf(x)Pacf(x)auto.arima(x,ic = "bic")## Series: x
## ARIMA(1,0,2)(1,0,0)[12] with zero mean
##
## Coefficients:
## ar1 ma1 ma2 sar1
## 0.4648 -0.2850 0.4401 -0.0243
## s.e. 0.0766 0.0738 0.0418 0.0455
##
## sigma^2 estimated as 0.8746: log likelihood=-675.65
## AIC=1361.29 AICc=1361.41 BIC=1382.37Nesse caso o auto.arima acertou, mas nem sempre isso ocorre.
VARs
Um VAR, teoricamente, é apenas uma generalização do AR. Ainda assim, do ponto de vista computacional, eles são distintos, e o VAR tem seu próprio conjunto de pacotes no R. O mais importante deles é o vars.
Começamos juntando todas as séries que queremos estimar o VAR em uma matriz (use o cbind() para isso). O passo seguinte é escolher a ordem do VAR - geralmente usando algum critério de informação. O comando VARselect faz isso e apresenta alguns critérios de informação e a quantidade de lags que minimizam cada um.
O comando que faz a estimativa per se é o VAR. Ele recebe a matriz com as séries e quantos lags você quer que sejam usados - ou o critério de informação a ser usado na hora de fazer a estimativa.
Por último, queremos recuperar a resposta dinâmica de cada uma das variáveis a um choque (não só um choque na própria variável, como o efeito cruzado de um choque em outra variável).
Vamos gerar um VAR(1) com duas variáveis apenas para ilustrar o uso do pacote:
library(vars)
T <- 500 #número de períodos
N <- 2 #número de variáveis
u <- matrix(rnorm(T*N),nrow = N,ncol = T)
x <- matrix(0,nrow = N, ncol = T)
A <- rbind(c(0.3,-0.2),c(0.6,0.2))
for(j in 2:T){
x[,j] <- A%*%x[,j-1] + u[,j]
}
x <- x[,400:500]
x <- t(x)
colnames(x) <- c("x","y")
VARselect(x) ## $selection
## AIC(n) HQ(n) SC(n) FPE(n)
## 1 1 1 1
##
## $criteria
## 1 2 3 4 5 6 7 8 9 10
## AIC(n) 0.5073838 0.5664775 0.6364448 0.7148971 0.8004834 0.804686 0.8853781 0.9301667 0.9188877 0.9939262
## HQ(n) 0.5741733 0.6777934 0.7922872 0.9152658 1.0453785 1.094108 1.2193260 1.3086411 1.3418885 1.4614533
## SC(n) 0.6729349 0.8423961 1.0227309 1.2115506 1.4075043 1.522074 1.7131339 1.8682901 1.9673785 2.1527844
## FPE(n) 1.6610195 1.7624397 1.8909018 2.0466301 2.2319134 2.244812 2.4386605 2.5575410 2.5379366 2.7479537modelo <- VAR(x,p = 1)
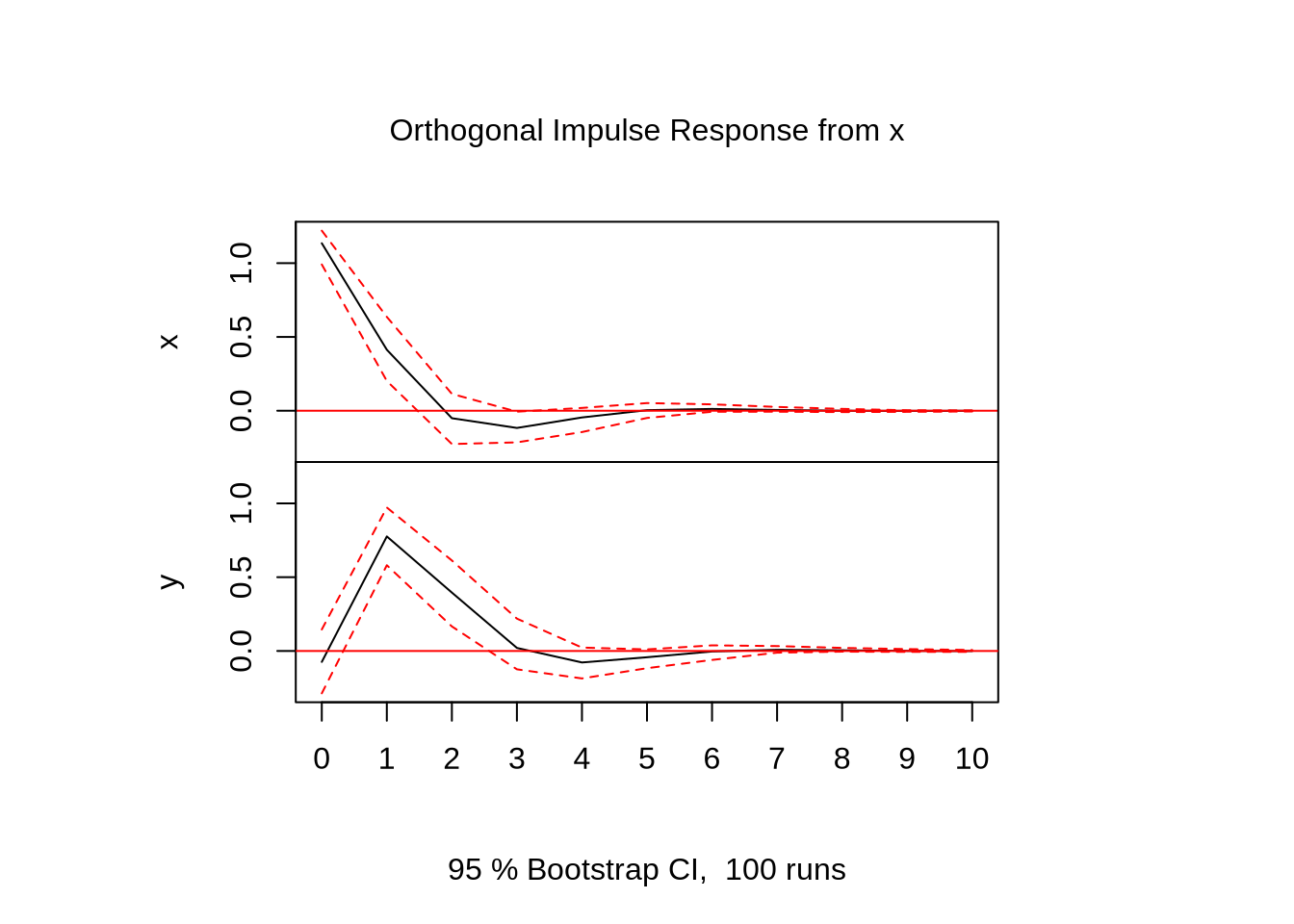
plot(irf(modelo, impulse = "x", response = c("x","y")))Eu só pedi o plot do choque da primeira variável sobre as duas variáveis por que isso é uma ilustração. Fazer plot(irf(modelo)) em uma seção do R, ele vai plotar os choques de todas as variáveis sobre todas as variáveis.
Raiz unitária
O pacote urca nos trás testes de raiz unitária. O teste Dickey-Fuller, um dos mais populares, é chamado pelo ur.df(). Vamos gerar um passeio aleatório para mostrar:
x <- cumsum(rnorm(1000))
summary(ur.df(x))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression none
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.0769 -0.7404 -0.0143 0.6389 3.4537
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## z.lag.1 -2.254e-05 7.896e-04 -0.029 0.977
## z.diff.lag -1.212e-02 3.169e-02 -0.383 0.702
##
## Residual standard error: 1.001 on 996 degrees of freedom
## Multiple R-squared: 0.0001483, Adjusted R-squared: -0.001859
## F-statistic: 0.07388 on 2 and 996 DF, p-value: 0.9288
##
##
## Value of test-statistic is: -0.0285
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau1 -2.58 -1.95 -1.62Veja que o valor crítico para o teste Dick Fuller não é o valor usual da estatística t, mas sim o valor exibido na parte debaixo da tabela do sumário do teste. Nesse caso, a qualquer nível de significância, nós não rejeitamos a hipótese de raiz unitária. Vamos testar para um caso estacionário:
u <- rnorm(2000)
y <- rep(0,2000)
for(i in 2:2000){
y[i] <- 0.5*y[i-1] + u[i]
}
y <- y[1000:2000]
summary(ur.df(y))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression none
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.7812 -0.6434 0.0092 0.6571 3.2324
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## z.lag.1 -0.501212 0.031742 -15.790 <2e-16 ***
## z.diff.lag -0.002658 0.031612 -0.084 0.933
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9926 on 997 degrees of freedom
## Multiple R-squared: 0.2511, Adjusted R-squared: 0.2496
## F-statistic: 167.1 on 2 and 997 DF, p-value: < 2.2e-16
##
##
## Value of test-statistic is: -15.7901
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau1 -2.58 -1.95 -1.62Desassonalizando
Dados de séries temporais, não raramente, apresentam sazonalidade. Por exemplo, gasto de energia elétrica tende a ser maior nos meses de dezembro a fevereiro, devido ao verão. Retirar sazonalidade é importante em muitas análises.
Um método padrão é colocar dummies para as unidades de tempo (uma para cada mês se o dado for mensal, uma para cada trimestre se for trimestral etc) e usar o resíduo dessa regressão somado a média da série (já que o resíduo tem média zero, por construção). Criar as dummies “no braço” pode ser tedioso, mas felizmente o pacote forecast trás o comando seasonaldummy() que cria as dummies automaticamente para a série.
energia <- BETSget(1406, from = "2002-01-01")
dum <- seasonaldummy(energia)
mod <- Arima(energia, xreg = dum)
des <- resid(mod) + mean(energia)
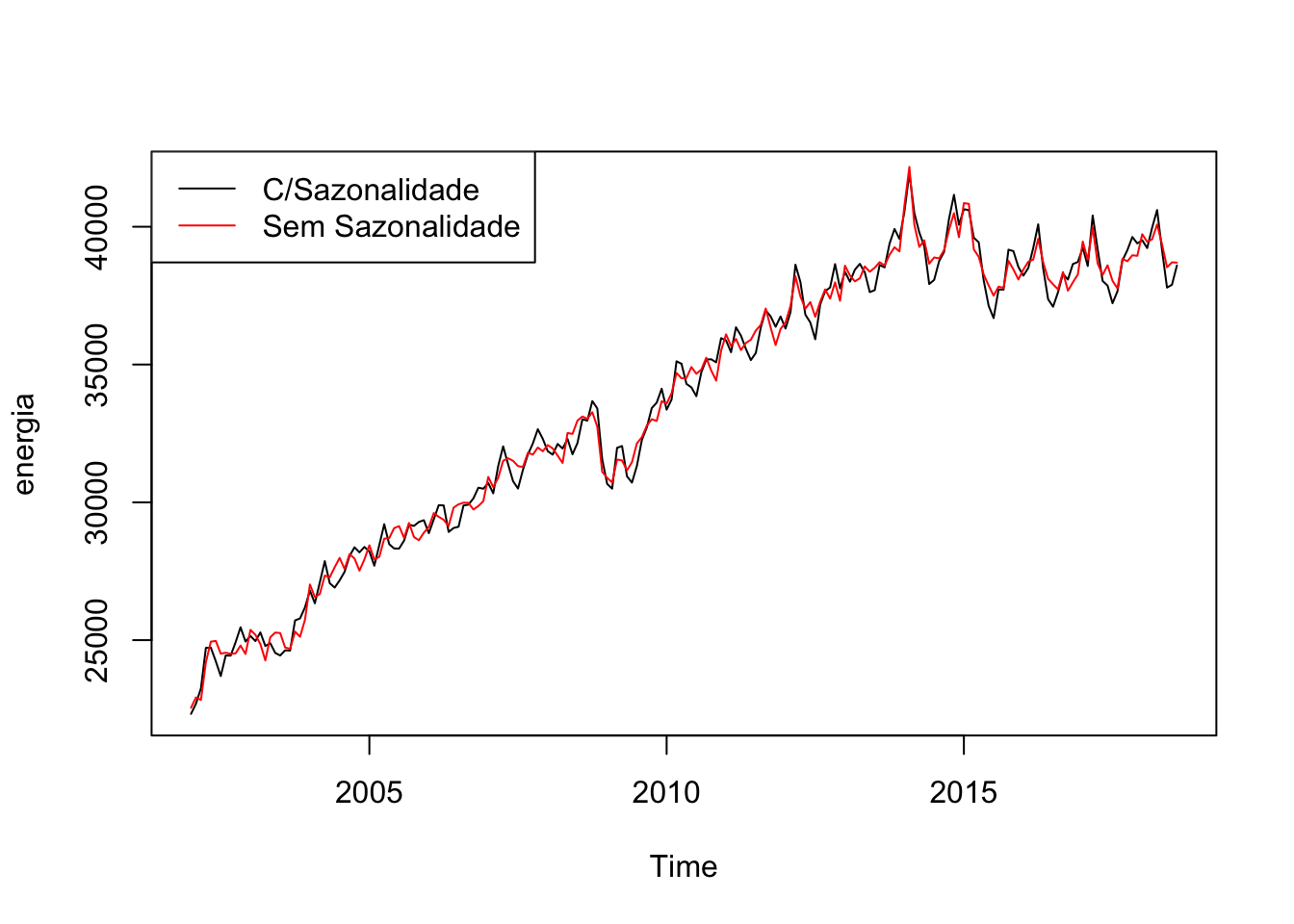
plot(energia)
lines(des, col = 2)
legend("topleft", legend = c("C/Sazonalidade", "Sem Sazonalidade"), lty = c(1,1), col = c(1,2))Outra maneira comum de dessazonalizar é usando o X13, um programa do governo americano. O X13 pode ser acessado direto do R usando o pacote seasonal. O comando que acessa o X13 é o seas. O X13 são, na verdade, dois programas: um que é o X13 e o outro que é o SEATS. Ambos tem a mesma função: dessazonalizar. O X13 vem com todo tipo de método automático para detectar outliers, fazer transformações nas séries e uma infinidade de outras coisas. Nesse caso, nós vamos desligar todas essa opções:
library(seasonal)
modelo2 <- seas(energia, transform.function = "none", regression.aictest = NULL, outlier = NULL)O comando final obtém a série dessazonalizada:
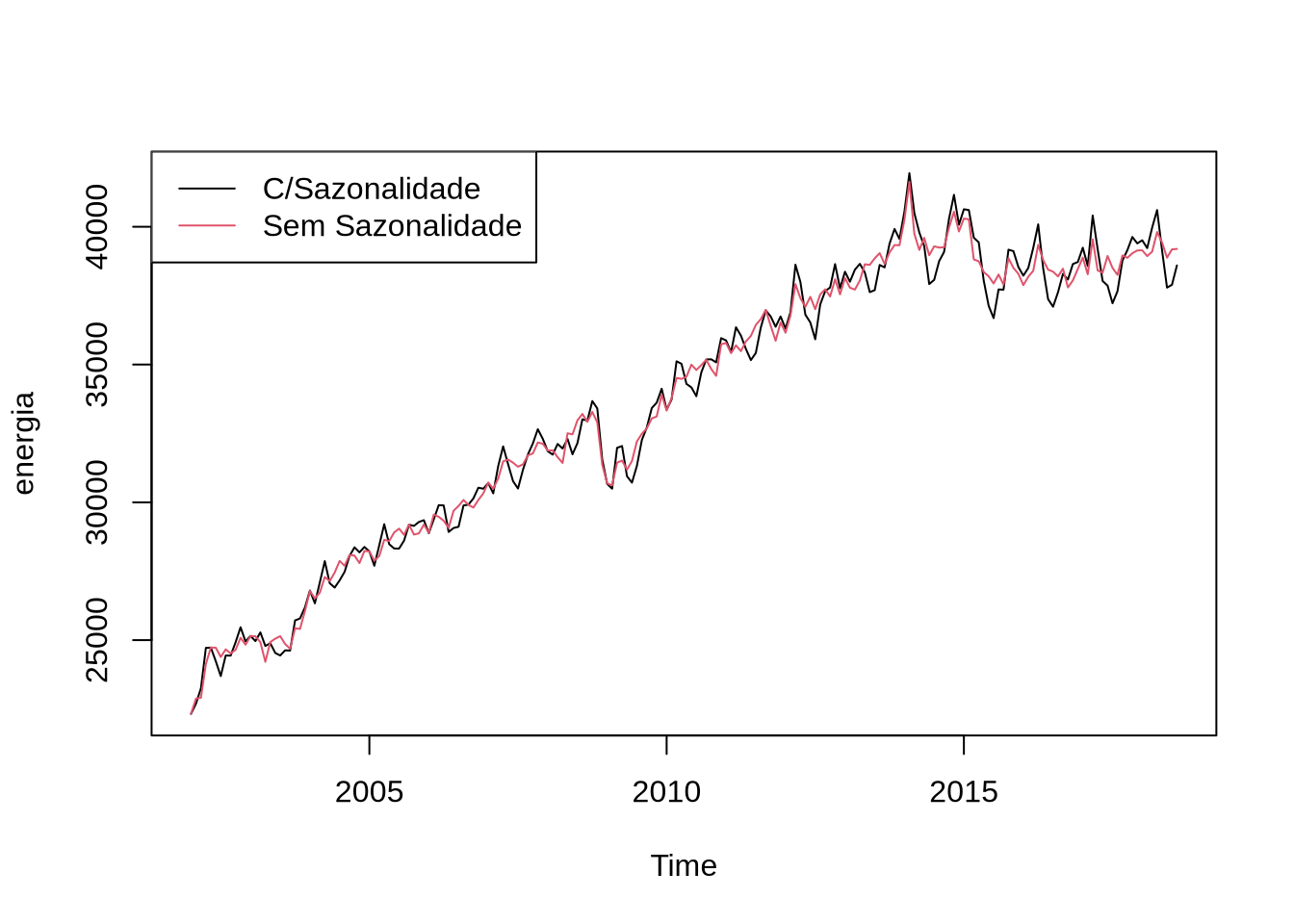
plot(energia)
lines(final(modelo2), col = 2)
legend("topleft", legend = c("C/Sazonalidade", "Sem Sazonalidade"), lty = c(1,1), col = c(1,2))Filtro Hodrick-Prescott
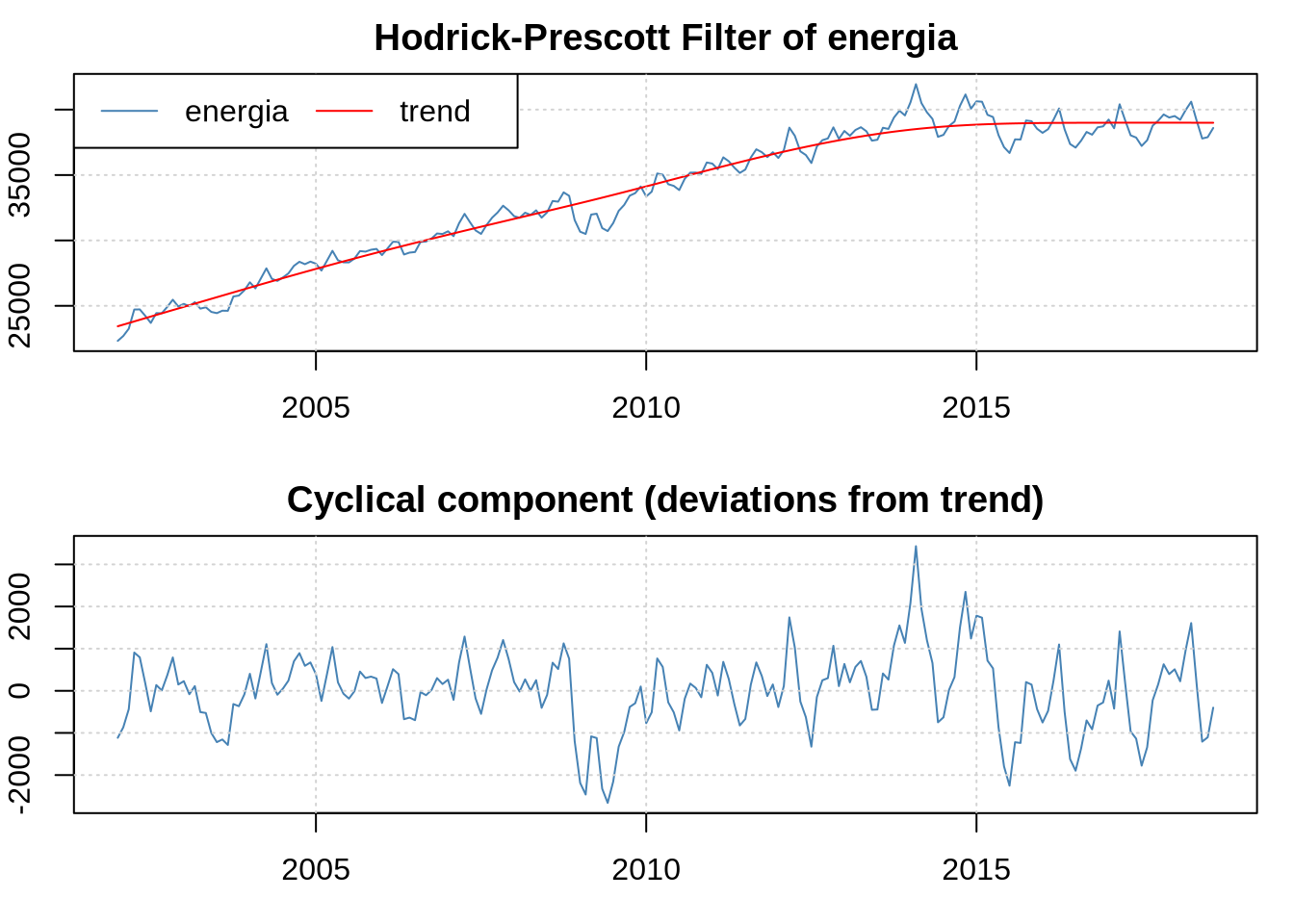
O filtro Hodrick-Prescott (HP) é utilizado em séries não estacionárias quando queremos separar a tendência do componente ciclíco. Ele é polêmico, mas ainda é amplamente usado. No R, o pacote mFilter implementa ele e alguns outros. Vamos aplicar na série de energia:
library(mFilter)
filtrado <- mFilter(energia, "HP")
plot(filtrado)Eu posso acessar a tendência e o componente cíclico usando o filtrado$trend e filtrado$cycle, no exemplo acima - que seria particularmente útil se eu quisesse utilizar os dados de cíclo para alguma estimação.