Surgimento da Física Moderna

Átomos e moléculas

Origens da visão atômica da matéria

Embora a nossa percepção nos apresente a matéria como contínua, a noção de que ela poderia na verdade ser constituída de corpúsculos demasiadamente pequenos para serem enxergados individualmente já tinha surgido na antiguidade, tanto na civilização occidental como na oriental.

Na Grécia, os filósofos Leucippus¹ e Democritus² são tidos pelos historiadores como “atomistas”, embora nenhum dos seus escritos tenha chegado até nós. Apenas podemos apreciar as suas idéias através de relatos escritos por outros, em especial a obra De Rerum Natura (Sobre a Natureza das Coisas) do poeta epicuriano Lucretius³.

A preocupação central que parece ter levado pensadores antigos a postular a existência de átomos foi a necessidade de conciliar as capacidades de transformação da matéria com a noção de permanência do universo. Os átomos⁴ teriam algumas propriedades imutáveis, tais como tamanho e peso, mas nenhuma estrutura. Haveria espaço vazio (“vácuo”) entre os átomos.

Deve-se enfatizar que não havia qualquer base experimental para estas idéias que, por mais premonitórias que possam ter sido, não passavam de especulações. Por esta razão, elas podiam facilmente ser derrubadas por outras, igualmente arbitrárias. Isto se deu de fato com o domínio da filosofia de Aristote⁵, que rejeitava a noção de vácuo.

A partir de Aristote e até a Renascência, apenas figuras marginais - e perseguidas pela Igreja Católica, que considerava as idéias de Aristote como dogma cientifíco - especularam sobre átomos. A visão atômica foi reabilitada no século XVI por Gassendi⁶, que procurou reconciliá-la com o dogma cristão. Talvez não seja mera coincidência que, na mesma época, foram desenvolvidos métodos para criar vácuo, tais como o barômetro de Torricelli e a bomba de ar.

[1] Leucippus, filósofo grego.
[2] Democritus, filósofo grego, -460-370.
[3] Lucretius, poeta e filósofo romano, -97-54.
[4] Do grego "a-tomo", aquilo que não pode ser dividido.
[5] Aristote, filósofo grego, -384-322.
[6] Pierre Gassendi, filósofo e cientista francês, 1592-1655.

Átomos químicos

A transformação da noção filosófica de átomo em conceito científico deve-se em grande parte ao desenvolvimento da química.

Ao serem misturadas, substâncias químicas usualmente formam uma substância que possui propriedades intermediárias em comparação com as das substâncias iniciais. Por exemplo, ao misturar-se açucar com água, em proporções quaisquer, obtem-se água adocicada, na qual as características tanto do açucar como da água estão obviamente presentes. Tal fato sugere fortemente que as espécies químicas, açucar e água, permanecem presentes na mistura. Isto por sua vez seria difícil de conciliar com uma visão contínua da matéria, mas é facilmente entendido numa visão corpuscular, na qual os corpúsculos de água e de açucar convivem na mistura, mantendo a sua individualidade. Substâncias químicas puras são aquelas que não podem ser separadas em componentes por processos físicos tais como centrifugação, evaporação ou distilação. É razoável supor que os corpúsculos que constituem uma substância pura são todos idênticos, pois senão seria possível produzir variedades desta substância. Outra hipótese simplificadora que tem-se revelada correta é que os corpúsculos que constituem uma dada substância pura são os mesmos nos vários estados nos quais a substância pode ser encontrada. Por exemplo, um corpúsculo de água líquida é idêntico a um corpúsculo de vapor de água.

Já numa reação química, as propriedades dos produtos são geralmente muito diferentes das propriedades dos reagentes. Mesmo assim, o estudo das reações químicas tem trazido evidências inconfundíveis da existência de espécies químicas discretas.

Robert Boyle⁷, na sua obra The Skeptical Chymist (O Químico Cético) foi talvez o primeiro cientista a distinguir entre as substâncias compostas e os elementos que as compõem. Esta distinção foi melhor estabelecida por Lavoisier⁸ que, em 1774, estabeleceu a lei da conservação das massas dos elementos nas reações químicas. Ele enfatizou a possibilidade de recuperar um elemento na sua forma e quantidade iniciais após combinação com outros de várias maneiras, o que evidenciava a permanência dos corpúsculos que constituem os elementos. Não há transmutação de um elemento para outro.Veja um exemplo.

A lei de formação dos compostos foi durante muito tempo objeto de controvérsia . Ainda no começo do século XIX, o influente químico Berthollet⁹ acreditava que as proporções de elementos que formiam um composto podiam depender das quantidades inicialmente presentes. Porém, em 1807, Proust¹⁰ estabeleceu a lei das proporções constantes, a qual afirma que numa reação química, as razões entre massas de reagentes que se combinam não podem variar de maneira contínua. A partir de reagentes dados, é possível em geral formar mais de um produto, mas para cada um deles,, estas razões são sempre as mesmas, independentemente das quantidades envolvidas e do procedimento utilizado. Experimentos mais elaborados levaram Dalton¹¹ a formular a lei das proporções múltiplas, que podemos enunciar como segue: se considerarmos duas espécies químicas S1 e S2 contendo os elementos A e B, e denotarmos por M_A1 e M_A2 as massas do elemento A que se combinam nelas com uma dada massa M_B do elemento B, então verifica-se que

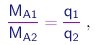(1-1)

onde q₁ e q₂ são números inteiros pequenos, independentes de M_B. Por exemplo, se considerarmos o monóxido de carbono e o gás carbônico, as massas de oxigênio que se combinam nestas substâncias com uma dada massa de carbono estão na razão 1/2.

Para explicar as suas observações, Dalton formulou um conjunto de hipóteses que constituem o fundamento da teoria atômica e molecular moderna, e que listamos a seguir.

• Os elementos são constituídos de átomos. Todos os átomos de um dado elemento são idênticos; em especial, possuem a mesma massa. Átomos de elementos diferentes possuem massas diferentes.
• Os átomos não podem ser criados nem destruídos, eles apenas sofrem rearrranjo nas reações químicas. Assim fica explicada a lei de Lavoisier.
• Os corpúsculos de uma substância pura composta são moléculas constituídas de átomos dos elementos que a compõem.

Assim, a molécula de uma substância S que contem os elementos A e B será constituída de a átomos de A e átomos b de B. Sendo m_A e m_B as massas destes átomos, a massa da molécula será

(1-2)

e para preparar uma quantidade da substância S contendo N moléculas, as massas de A e B necessárias estarão na razão

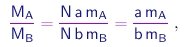(1-3)

independente de N, conforme exige a lei de Proust.

As massas das moléculas de duas substâncias puras S₁ e S₁ contendo A e B serão dadas por expressões do tipo (1-2), com coeficientes a₁,b₁ e a₂,b₂, respectivamente. Portanto, as massas de A que se combinarão com uma massa de B contendo N_B átomos, para formar as substâncias S₁ e S₂, serão dadas por

e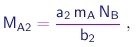

(1-4)

respectivamente. Vê-se que

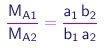(1-5)

é a razão de dois inteiros. Assim, a lei de Dalton também é satisfeita.

Embora os trabalhos de Dalton constituam-se num grande avanço, eles não permitiram a determinação correta dos números de átomos que compunham as moléculas de todas as espécies químicas conhecidas naquela época. A informação que faltava veio do estudo dos gáses e das suas reações. Na sua forma original, a lei dos gáses de Boyle e Mariotte¹² afirma que, a temperatura T fixa, a densidade de massa varia proporcionalmente à pressão. Também foi observado por Gay-Lussac¹³ e Charles¹⁴ que, à pressão p fixa, a densidade varia em proporção inversa da temperatura. Evidentemente, para uma substância pura, a densidade de massa é proporcional à densidade de moléculas n. Portanto, pode-se escrever

(1-6)

onde k é uma constante que, nesta altura do nosso desenvolvimento, pode depender da substância considerada. Se compararmos dois gáses nas mesmas condições de temperatura e pressão, concluimos que a razão entre as densidades de moléculas,

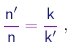(1-7)

é invariante frente a modificações de pressão ou temperatura.

Ao estudar as reações químicas entre substâncias gasosas, Gay-Lussac estabeleceu em 1808 a lei dos volumes, a qual afirma que as quantidades de substâncias que participam numa reação, quando trazidas para as mesmas condições de temperatura e pressão, ocupam volumes que estão em razões simples. Em especial, se considerarmos a decomposição de uma substância S em duas substâncias S' e S'', os volumes ocupados por elas satisfazem as relações

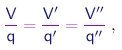(1-8)

onde q, q', q'' são números inteiros pequenos e independentes da quantidade de substância S considerada. Veja um exemplo.

Para explicitar o significado desta lei na teoria atômica, supomos que as substâncias S e S', mas não a substância S'', contém um dado elemento A. Sejam a e a' os números de átomos de A presentes numa molécula de S e de S', respectivamente. Sejam N e N' os números de moléculas de S e S' envolvidas na reação. Então, pela conservação dos átomos, temos

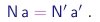(1-9)

Usando as relações acima, podemos escrever

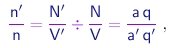(1-10)

ou seja, a razão entre as densidades de moléculas, além de invariante, deve ser uma fração simples. Generalizando a relação acima a vários compostos contendo o elemento A, podemos escrever

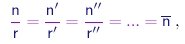(1-11)

onde r, r', r'' são números inteiros e denotamos por n o valor comum destas razões. Em determinadas condições de temperatura e pressão, a massa de elemento A contida num volume de referência V de um deste compostos será

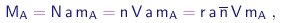(1-12)

múltiplo do “quantum de massa” n V m_A. Ao medirmos estes “quanta” para todos os elementos conhecidos, poderemos determinar as razões entre as massas dos seus átomos. A primeira determinação precisa dos pesos atômicos relativos - de cerca de 40 elementos conhecidos na época – foi realizada por Berzelius¹⁵.

O último passo neste desenvolvimento foi dado por Avogadro¹⁶ ao enunciar as sua famosa hipótese: a densidade de moléculas em determinadas condições de pressão e temperatura é independente do gás considerado:

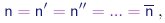(1-13)

ou ainda, os números inteiros r, r'... introduzidos acima são sempre iguais à unidade e podemos denotar a densidade de moléculas simplesmente por n, independente do gás considerado. Sendo a razão (1-10) sempre igual à unidade, podemos escrever

(1-14)

ou seja, a medida da razão entre os volumes de gases envolvidos numa reação permite relacionar diretamente os números de átomos contidos nas suas moléculas. Veja um exemplo.

Notamos também que, com a hipótese de Avogadro, a constante k presente na lei dos gáses (1-6) é na verdade uma constante universal, a constante de Boltzmann.

Usando esta hipótese, é possível determinar as razões entre as massas das moléculas de elementos gasosos. Por exemplo: 10 l de H a 0^o C e 1 atm tem massa 0,892 g e 10 l de O nas mesmas condições 14,3 g. Daí 14,3 / 0,892 = 16. É curioso que muitos dos erros cometidos por Dalton ao tentar estabelecer as estruturas moleculares originaram-se na suposição que as moléculas dos elementos eram monoatômicas. Com a sua hipótese, Avogadro endireitou a questão, mas passaram-se muitos anos até que a importância desta contribuição seja geralmente reconhecida, principalmente graças aos esforços de Cannizzaro¹⁷.

Como discutido acima, os “quanta atômicos” são proporcionais ao número de moléculas que eles contém. Para defini-los completamente, uma convenção é portanto necessária. Seria natural escolher o mais leve dos elementos, hidrogênio, como referência e definir o quantum atômico tal que ele seja igual a 1 g para este elemento. Por razões técnicas, a convenção atualmente adotada é ligeiramente diferente: o quantum atômico, denominado mol, é definido tal que vale exatamente 12 g para o elemento carbono usual¹⁸. O valor de correspondente recebe merecidamente o nome de número de Avogadro, que denotaremos por N_A. O quantum atômico associado a N_A átomos de um elemento é o peso atômico daquele elemento.

Vale notar que, se soubermos o valor de N_A, poderemos determinar a massas dos átomos a partir dos valores correspondentes dos pesos atômicos. Vice-versa, se conhecermos o valor da massa do átomo de um elemento, poderemos deduzir do seu peso atômico o valor de N_A, e daí calcular as massas de todos os demais átomos a partir dos seus pesos atômicos. Porém, nem a massa de um átomo, nem o número de Avogadro são quantidades fáceis de serem determinadas experimentalmente.

[7] Robert Boyle, químico e físico inglés, 1627-1691.
[8] Antoine Laurent Lavoisier, químico francês, 1749-1794.
[9] Berthollet, químico francês.
[10] Jean Louis Proust, químico francês, 1755-1826.
[11] John Dalton, físico e químico inglés, 1766-1844.
[12] Edme Mariotte, físico francês, -1684.
[13] Joseph Louis Gay-Lussac, físico e químico francês, 1778-1850.
[14] A. C. Charles, físico francês, 1746-1823.
[15] Jöns Jakob Berzelius, químico sueco, 1779-1848.
[16] Amedeu Avogadro, físico e químico italiano, 1776-1856.
[17] Stanislao Cannizzaro, químico italiano, 1826-1910.
[18] Como será discutido adiante neste curso, existem vários isótopos de carbono, átomos com propriedades químicas idênticas porém massas diferentes.

Teoria cinética dos gases

Uma vez aceito que a matéria é composta de átomos e moléculas, tem-se um novo ponto de partida na tarefa de explicar as suas propriedades. É natural começar pelo estudo do estado gasoso, no qual as moléculas estão muito distantes uma da outra a maior parte do tempo. Neste caso pode-se esperar que o conhecimento detalhado das interações entre moléculas não seja necessário para se obter uma descrição adequada.

Se concerbermos um gás como um conjunto de moléculas livres, apenas confinadas pelas paredes do recipiente que as contém, poderemos explicar a pressão aplicada pelo gás sobre uma parede como resultante das colisões com esta das moléculas dos gás. É conveniente supor que o recipente seja um cubo de lado L.

Na colisão de uma molécula de massa m com uma parede perpendicular ao eixo x, a componente p_x = m v_x do momentum linear trocará de sinal. Pela conservação do momentum, uma quantidade de momentum

(1-15)

será transferida à parede. O intervalo entre colisões sucessivas desta molécula com esta parede será Dt = 2 L / v_x e portanto a taxa de transferência de momentum, ou ainda, a força aplicada pela molécula sobre a parede será

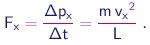(1-16)

Para obter a pressão sobre a parede basta multiplicar este resultado pelo número N de moléculas no recipiente, dividir pela área L² da face do cubo e tomar a média, pois a velocidade pode variar de uma molécula para outra. Assim obtemos

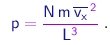(1-17)

Como as três direções são equivalentes, temos obviamente v_x² = v_y² = v_z² = v² / 3 e chegamos ao resultado

(1-18)

onde introduzimos a densidade de massa r = N m / L³ = M / V.

A energia cinética média por molécula é

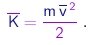(1-19)

Portanto, já que estamos desprezando as energias potenciais de interação entre moléculas, a densidade de energia é dada por

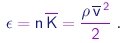(1-20)

Concluimos que a teoria cinética dos gáses prevê a simples relação

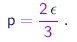(1-21)

Utilizando agora a lei dos gáses (1-5), podemos re-escrever esta relação na forma

(1-22)

ou

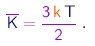(1-23)

Assim, a energia cinética média por molécula dos gás depende apenas da temperatura. Em especial, é independente da massa das moléculas. Temos aqui um exemplo de um fato mais geral, conhecido como princípio de equipartição da energia, que afirma que, num sistema em equilíbrio térmico à temperatura , a energia cinética média associada a cada grau de liberdade vale kT/2. No caso de moléculas em movimento de translação no espaço tridimensional, são evidentemente três os graus de liberdade. Faremos uso deste princípio em outro contexto mais adiante.

Dimensões atômicas e número de Avogadro

As massas e os tamanhos atômicos e moleculares, assim como os números destes corpúsculos presentes num dado volume, são as quantidades que caracterizam a descrição corpuscular da matéria. Evidentemente, elas estão relacionadas por observações feitas a nível “macroscópico”. Por exemplo, no estado condensado (líquido ou sólido) se soubermos quantas moléculas há num determinado volume, poderemos determinar o seu tamanho e, a partir da densidade do matérial, a massa de cada molécula. Assim, é de fundamental importância a determinação de uma destas grandezas, por exemplo o número de moléculas num mol.

A teoria cinética dos gáses fundamentou a primeira determinação experimental do número de Avogadro, realizada em 1865 por Loschmidt¹⁹, que se valeu de resultados teóricos obtidos por Maxwell²⁰ e Clausius²¹.

As moléculas de um gás são livres apenas em primeira aproximação. Mesmo num gás bastante diluído, uma molécula ocasionalmente encontra uma outra molécula e sofre colisão. O livre caminho médio l é a distância média percorrida por uma molécula entre colisões.

Colisões são também responsáveis pelo fato que uma camada de gás em movimento em relação a outra irá arrastar esta no seu movimento. Este é o fenômeno de viscosidade. O coeficiente de viscosidade h é definido como a força tangencial exercida por uma camada sobre uma superfície unitária da camada vizinha quando existe um gradiente de velocidade unitário, perpendicular ao fluxo de gás. Argumentaremos que o coeficiente de viscosidade é proporcional ao produto de três fatores:

1. a densidade r do gás. Isto é natural já que quanto mais massivas e mais numérosas (por unidade de volume) as moléculas, maior será o efeito do seu impacto com as moléculas da camada vizinha.
2. a velocidade média v das moléculas. Isto também é facilmente entendido, já que o momentum das moléculas determina a intensidade do impacto.
3. o livre caminho médio l das moléculas. Talvez isto seja menos intuitivo, mas um pouco de reflexão nós faze entender que, quanto maio for, mais distante da camada impactada será a camada da qual a molécula originou-se. Portanto, em razão do gradiente transversal no fluxo do gás, maior será a diferença de velocidade entre as moléculas que sofrem a colisão, e maior será o efeito da mesma.

Um cálculo detalhado leva ao resultado

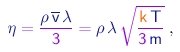(1-24)

onde usamos as relações (1-19) e (1-23) para expressar a velocidade média das moléculas em termos da massa das mesmas e da temperatura do gás.

Temos até aqui duas quantidades incognitas ( l e m ) e precisamos obter uma outra relação. Imaginamos as moléculas como esferas de diâmetro D que colidem como bolas de gude, e focamos o movimento de uma delas, considerando em primeira aproximação as outras como fixas no espaço. Supomos que a molécula considerada acaba de sofrer uma colisão. Para ser a próxima atingida, uma molécula deve ter o seu centro a uma distância máxima D da linha de movimento da molécula considerada. Portanto, deve encontrar-se dentro de um cilindro cujo eixo coincide com a linha de movimento da molécula focada, cujo raio é D e cujo comprimento é l, já que esta é a distância percorrida entre colisões. Ou seja, o volume p D²l deste cilindro deve conter na média uma molécula. Levando-se em conta o movimento das moléculas, mostra-se que este volume deve ser multiplicado por 2^1/2 , de maneira que a relação correta é

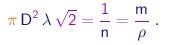(1-25)

Utilizando o resultado acima para eliminar o produto l r da expressão (1-24), obtemos

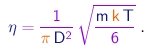(1-26)

É interessante notar que a viscosidade de um gás revela-se independente da pressão neste modelo, dependendo apenas da temperatura. Este resultado um tanto surpreendente foi verificado em experimentos realizados pelo próprio Maxwell. Já que podemos medir a viscosidade, a equação acima estabelece uma relação entre a massa de uma molécula e o seu diâmetro:

(1-27)

Para obtermos uma outra relação entre estas quantidades, consideremos agora o estado condensado, no qual vamos supor que as as moléculas "se tocam", ocupando o menor volume possível. Sendo r_cond o valor (facilmente medido) da densidade neste estado, podemos escrever

(1-28)

O fator 4 / 3 foi introduzido para levar em conta, em boa aproximação, o espaço vazio entre moléculas, consideradas como bolas numa pilha. Pode-se mostrar que, nume pilha de bolas, cada bola ocupa um volume igual a aproximadamente 4/3 do seu próprio volume. De (1-27) e (1-28), tiramos uma estimativa para o diâmetro da molécula:

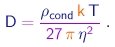(1-29)

Para poder aplicar este resultado, devemos utilizar uma substância cuja viscosidade no estado gasoso possa ser medida, e que possa ser trazida para o estado sólido ou líquido. Veja um exemplo.

Obviamente, devido às simplificaões feitas, não podemos esperar obter um valor preciso com este procedimento. Átomos e moléculas certamente não são esféras rígidas, e não necessariamente estão "empilhadas" da maneira mais eficiente no estado condensado. Apesar disto, a ordem de grandeza do raio atômico é corretamente estimada (veja o exemplo):

Rátomo ~ 10-10 m = 1 Å .

(1-30)

Encontraremos algumas outras maneiras de determinar o número de Avogadro no decorrer dos nossos estudos. Mencionamos aqui o movimento Browniano, que vem a ser o movimento aleatório realizado por uma parcela de matéria, pequena mas observável com a ajuda de um microscópio, imersa num líquido. Este efeito devido aos impactos sobre a parcela das moléculas do líquido em agitação térmica foi descoberto em 1827 por Brown²², analizado teoricamente por Einstein²³ e estudado experimentalmente principalmente por Perrin²⁴.

O valor atualmente aceito para o número de Avogadro é

NA = 6,02 1023 .

(1-31)

[19] Josef Loschmidt, físico tcheco, 1821-1895.
[20] James Clerck Maxwell, físico escocês, 1831-1879.
[21] Rudolf Julius Emanuel Clausius, físico alemão, 1822-1888.
[22] Robert Brown, botânico escocès, 1773-1858.
[23] Albert Einstein, físico alemão, 1879-1955.
[24] Jean Perrin, físico francês, 1870-1942.