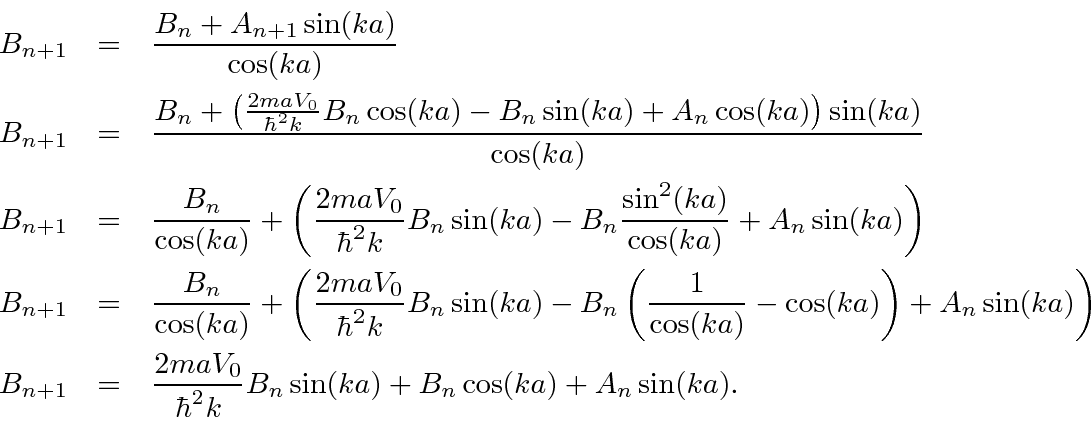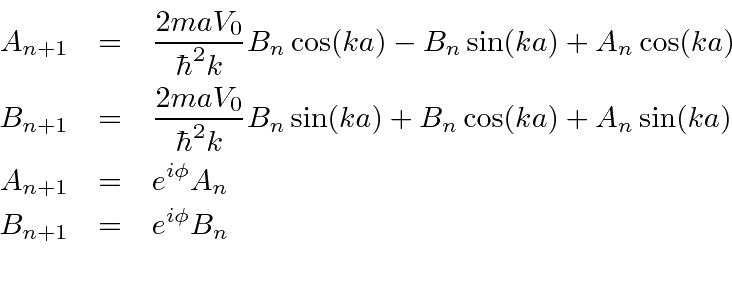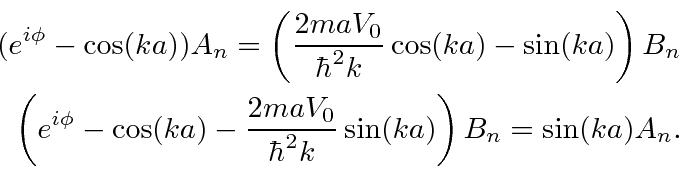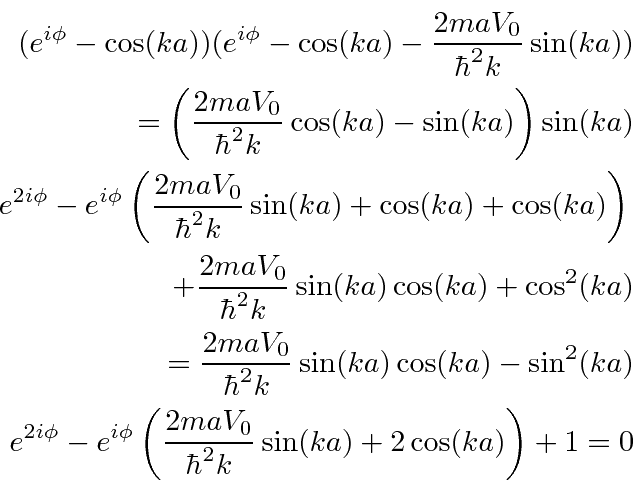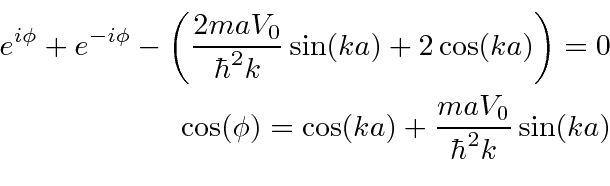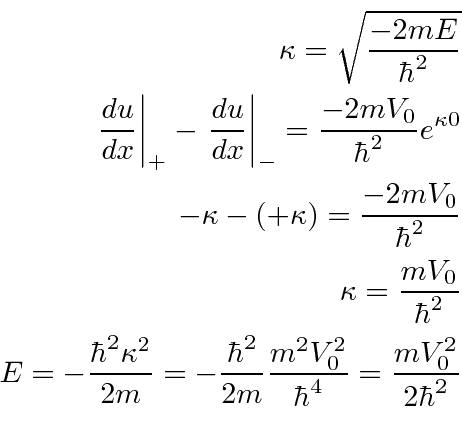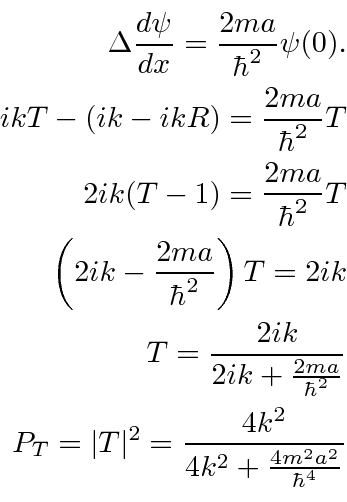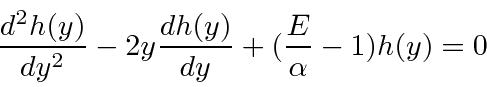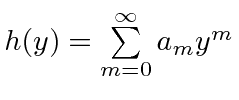Potenciais constantes por partes em 1D
Vários problemas padrão podem ser entendidos conceitualmente usando duas ou três regiões com potenciais constantes. Encontraremos soluções em cada região do potencial. Esses potenciais têm soluções simples para a equação de Schrödinger . Devemos então combinar as soluções nas fronteiras entre as regiões. Por causa das várias regiões, esses problemas exigirão mais trabalho com as condições de contorno do que o normal.
A solução geral para um potencial constante
Encontramos a solução geral da Equação de Schrödinger em uma região em que o potencial é constante. Suponha que o potencial seja igual a ![]() e a energia total seja igual a
e a energia total seja igual a ![]() . Suponha ainda que estamos resolvendo a equação independente do tempo.
. Suponha ainda que estamos resolvendo a equação independente do tempo.
com positivo e real. Também poderíamos usar a combinação linear das duas soluções acima. 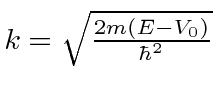
Devemos usar um ou outro conjunto de soluções em uma região, não ambos. Existem apenas duas soluções linearmente independentes.
As soluções também são tecnicamente corretas, 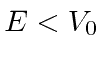 mas
mas ![]() se tornam imaginárias. Para simplificar, vamos escrever as soluções em termos de , o que novamente é real e positivo. A solução geral é
se tornam imaginárias. Para simplificar, vamos escrever as soluções em termos de , o que novamente é real e positivo. A solução geral é 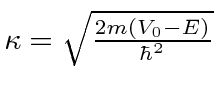
Não são ondas, mas exponenciais reais. Observe que essas são soluções para regiões onde a partícula não é permitida classicamente, devido à conservação de energia; a energia total é menor do que a energia potencial. No entanto, precisaremos dessas soluções em Mecânica Quântica.
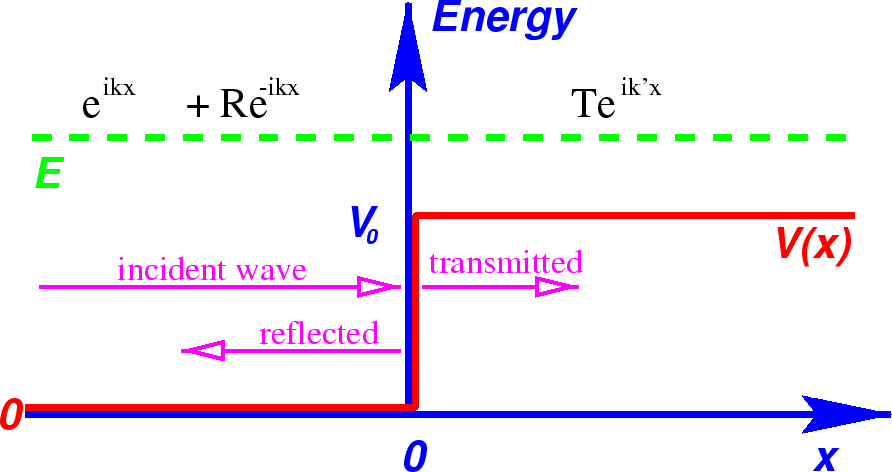
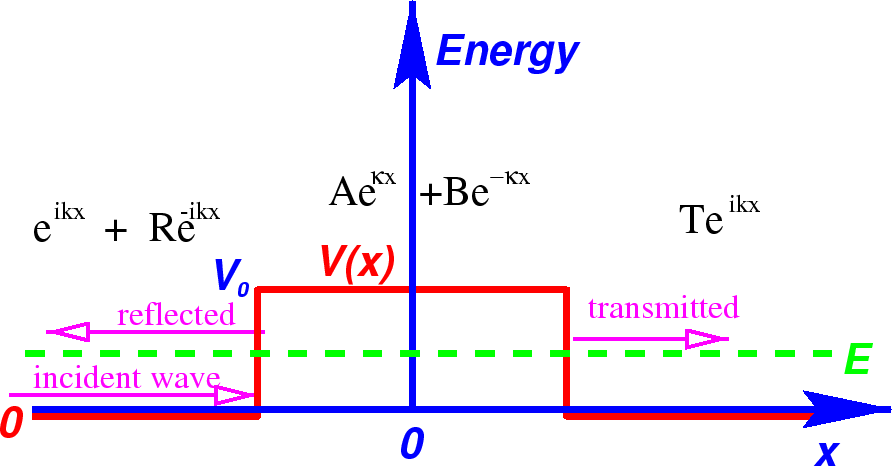
O Passo Potencial
Queremos estudar a física de uma etapa potencial para o caso 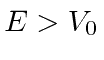 .
.
Para este problema, ambas as regiões o fizeram 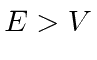 , então usaremos as soluções exponenciais complexas em ambas as regiões. Este é essencialmente um problema de espalhamento 1D. Suponha que haja um feixe de partículas com momento definido vindo da esquerda e suponha que não haja fluxo de partículas vindo da direita.
, então usaremos as soluções exponenciais complexas em ambas as regiões. Este é essencialmente um problema de espalhamento 1D. Suponha que haja um feixe de partículas com momento definido vindo da esquerda e suponha que não haja fluxo de partículas vindo da direita.
Observe que assumimos que o coeficiente do feixe incidente é 1. (Multiplicar por algum número não muda a física.) Pois 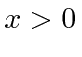 a solução é
a solução é
(Observe que um feixe vindo da direita, teria dado um ![]() termo para
termo para 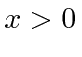 .)
.)
Existem dois coeficientes desconhecidos ![]() e
e ![]() que serão determinados combinando as condições de contorno. Não vamos exigir normalização para uma partícula, uma vez que temos um feixe com momento definido, que não pode ser normalizado dessa forma. (Um problema mais físico para resolver seria usar um pacote de ondas de entrada com uma propagação no momento).
que serão determinados combinando as condições de contorno. Não vamos exigir normalização para uma partícula, uma vez que temos um feixe com momento definido, que não pode ser normalizado dessa forma. (Um problema mais físico para resolver seria usar um pacote de ondas de entrada com uma propagação no momento).
Continuidade da função de onda a ![]() implica
implica
As exponenciais são todas iguais a 1 aqui, então a equação é simples.
Continuidade da derivada da função de onda em ![]() dá
dá
Avalie e conecte a ![]() partir da equação acima. Podemos resolver o problema.
partir da equação acima. Podemos resolver o problema.
Os coeficientes são
Agora temos a solução completa , dada nossa suposição de partículas incidentes a partir da esquerda.
Classicamente , todas as partículas seriam transmitidas, continuando até o infinito.
Na Mecânica Quântica, alguma probabilidade é refletida .
(Observe que podemos simplesmente usar o coeficiente de ![]() porque o termo de entrada tem um coeficiente de 1 e porque as partículas refletidas estão se movendo com a mesma velocidade do feixe de entrada.)
porque o termo de entrada tem um coeficiente de 1 e porque as partículas refletidas estão se movendo com a mesma velocidade do feixe de entrada.)
Se quisermos calcular a probabilidade de transmissão , a maneira fácil de fazer isso é dizer que é
Obteremos as mesmas respostas para os coeficientes de reflexão e transmissão usando o fluxo de probabilidade para resolver o problema.
A probabilidade de transmissão vai para 1 um ![]() (já que não há etapa). A probabilidade de transmissão vai para 0 para
(já que não há etapa). A probabilidade de transmissão vai para 0 para ![]() (já que a energia cinética é zero).
(já que a energia cinética é zero).
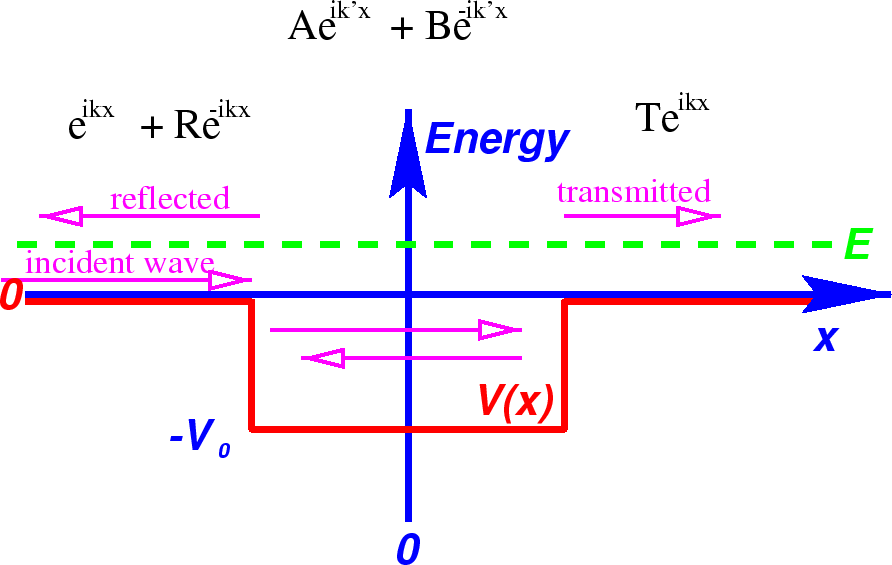
O Poço Potencial com *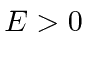
Com energia positiva, este é novamente um problema do tipo espalhamento, agora com três regiões do potencial, todas com 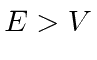 .
.
Numerando as três regiões da esquerda para a direita,
Mais uma vez, assumimos um feixe de impulso definido incidente da esquerda e nenhum incidente de onda da direita .
Existem quatro coeficientes desconhecidos . Agora combinamos a função de onda e sua primeira derivada nos dois limites, resultando em 4 equações .
Algum trabalho duro produz as amplitudes de reflexão e transmissão
Os quadrados destes fornecem a probabilidade de reflexão e transmissão , uma vez que o potencial é o mesmo nas duas regiões.
Novamente, classicamente, tudo seria transmitido porque a energia é maior do que o potencial. Mecanicamente quântico, existe uma probabilidade de ser transmitido e uma probabilidade de ser refletido. A probabilidade de reflexão irá para zero para certas energias : se ![]()
Existem análogos disso em 3D. A seção transversal de espalhamento freqüentemente vai para zero para certas energias particulares. Por exemplo, elétrons espalhando átomos podem ter seção transversal quase zero em alguma energia particular. Novamente, esta é uma propriedade da onda.
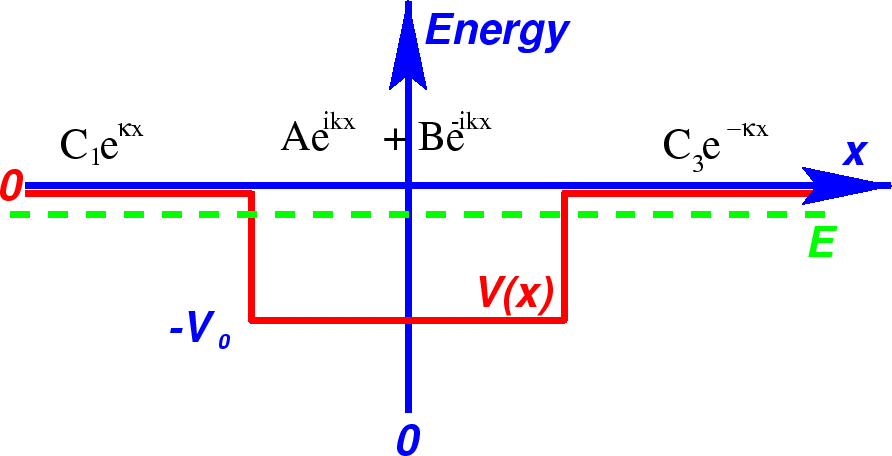
Estados vinculados em um poço potencial *
Trabalharemos com o mesmo potencial bem como na seção anterior, mas assumiremos isso 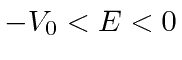 , tornando este um problema de estado limitado . Observe que esse potencial tem uma simetria de paridade. Nas regiões esquerda e direita, a solução geral é
, tornando este um problema de estado limitado . Observe que esse potencial tem uma simetria de paridade. Nas regiões esquerda e direita, a solução geral é
com
O ![]() termo não será aceitável em
termo não será aceitável em 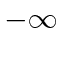 e o
e o ![]() termo não será aceitável em,
termo não será aceitável em, 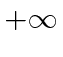 pois eles divergem e nunca poderíamos normalizar para uma partícula ligada.
pois eles divergem e nunca poderíamos normalizar para uma partícula ligada.
No centro, usaremos as soluções de seno e cosseno, antecipando os estados próprios de paridade.
Novamente, teremos 4 equações em 4 coeficientes desconhecidos.
O cálculo mostra que ![]() ou
ou ![]() deve ser zero para uma solução. Isso significa que as soluções se separam em estados de paridade par e paridade ímpar . Poderíamos ter adivinhado isso pelo potencial.
deve ser zero para uma solução. Isso significa que as soluções se separam em estados de paridade par e paridade ímpar . Poderíamos ter adivinhado isso pelo potencial.
Os estados pares têm a restrição (quantização) na energia que
e os estados ímpares têm a restrição
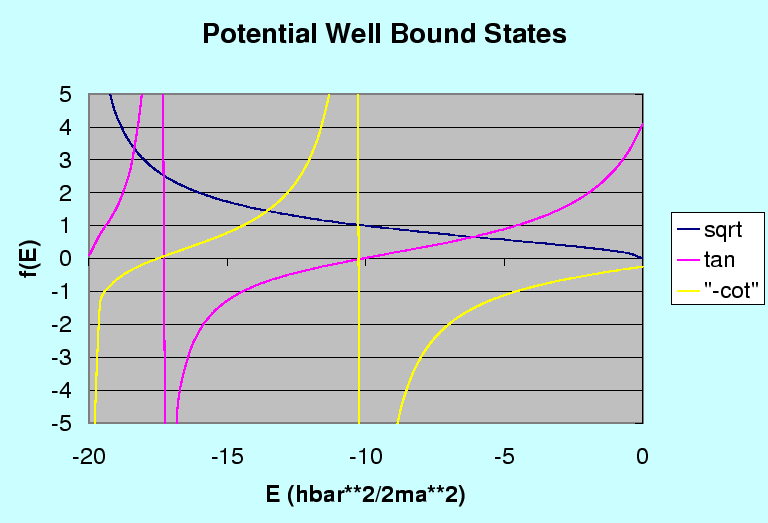
Essas são equações transcendentais, então vamos resolvê-las graficamente. O gráfico abaixo compara a raiz quadrada no lado esquerdo das equações transcendentais com a tangente à direita para os estados de evento e `` -cotangente '' à direita para estados ímpares. Onde as curvas se cruzam (não incluindo a assíntota), é uma energia permitida. Sempre há uma solução uniforme para o poço de potencial 1D. No gráfico mostrado, existem 2 soluções pares e uma ímpar. Quanto mais largo e profundo o poço, mais soluções.
A barreira potencial
Com uma análise do problema da Barreira Potencial, podemos entender o fenômeno do tunelamento quântico .
Numerando as três regiões da esquerda para a direita,
Mais uma vez, assumimos um feixe de incidente de momentum definido da esquerda e nenhum incidente de onda da direita. Para as soluções fora da barreira,
Dentro da barreira,
Este é realmente o mesmo que o problema de poço potencial (não ligado) com a substituição
na região centro.
A amplitude a ser transmitida é
Podemos calcular a probabilidade de ser transmitido.
Uma probabilidade aproximada às vezes é útil.
Classicamente, a probabilidade de transmissão seria zero . Na Mecânica Quântica, a partícula pode violar a conservação de energia por um curto período de tempo e, portanto, tem a chance de passar pela barreira.
O tunelamento pode ser aplicado à emissão fria de elétrons de um metal, decaimento alfa de núcleos, semicondutores e muitos outros problemas.
O oscilador harmônico 1D
O oscilador harmônico é um problema de física extremamente importante . Muitos potenciais parecem um oscilador harmônico próximo de seu mínimo. Este é o primeiro potencial não constante para o qual resolveremos a Equação de Schrödinger.
O oscilador harmônico hamiltoniano é dado por
o que torna a Equação de Schrödinger para autoestados de energia
Observe que esse potencial também tem uma simetria de paridade. O potencial não é físico porque não vai a zero no infinito; no entanto, costuma ser uma aproximação muito boa e esse potencial pode ser resolvido com exatidão.
É padrão remover a constante ![]() da mola do hamiltoniano, substituindo-a pela frequência clássica do oscilador .
da mola do hamiltoniano, substituindo-a pela frequência clássica do oscilador .
O Hamiltoniano do oscilador harmônico torna-se.
A equação diferencial a ser resolvida é
Para resolver a equação do oscilador harmônico, primeiro mudaremos para variáveis adimensionais, então encontraremos a forma da solução para , então, multiplicaremos essa solução por um polinômio, derivaremos uma relação de recursão entre os coeficientes do polinômio, mostraremos que a série polinomial deve terminar se as soluções devem ser normalizáveis, derivar os autovalores de energia e, finalmente, derivar as funções que são soluções. 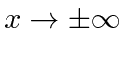
Os valores próprios de energia são
para 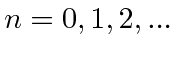 . Há um número infinito de soluções contáveis com espaçamento de energia igual . Fomos forçados a ter energias quantizadas pelo requisito de que as funções de onda sejam normalizáveis.
. Há um número infinito de soluções contáveis com espaçamento de energia igual . Fomos forçados a ter energias quantizadas pelo requisito de que as funções de onda sejam normalizáveis.
A função de onda do estado fundamental é.
Esta é uma distribuição gaussiana (incerteza mínima). Uma vez que o potencial HO tem uma simetria de paridade, as soluções têm paridade par ou ímpar . O estado básico é paridade par.
O primeiro estado excitado é um estado de paridade ímpar, com um polinômio de primeira ordem multiplicando o mesmo gaussiano.
O segundo estado excitado é paridade par, com um polinômio de segunda ordem multiplicando o mesmo gaussiano.
Observe que ![]() é igual ao número de zeros da função de onda. Esta é uma tendência comum. Com mais zeros, uma função de onda tem mais curvatura e, portanto, mais energia cinética.
é igual ao número de zeros da função de onda. Esta é uma tendência comum. Com mais zeros, uma função de onda tem mais curvatura e, portanto, mais energia cinética.
A solução geral pode ser escrita como
com os coeficientes determinados pela relação de recursão
e a variável adimensional ![]() dada por.
dada por.
A série termina com o último termo diferente de zero possuindo ![]() .
.
O potencial da função delta
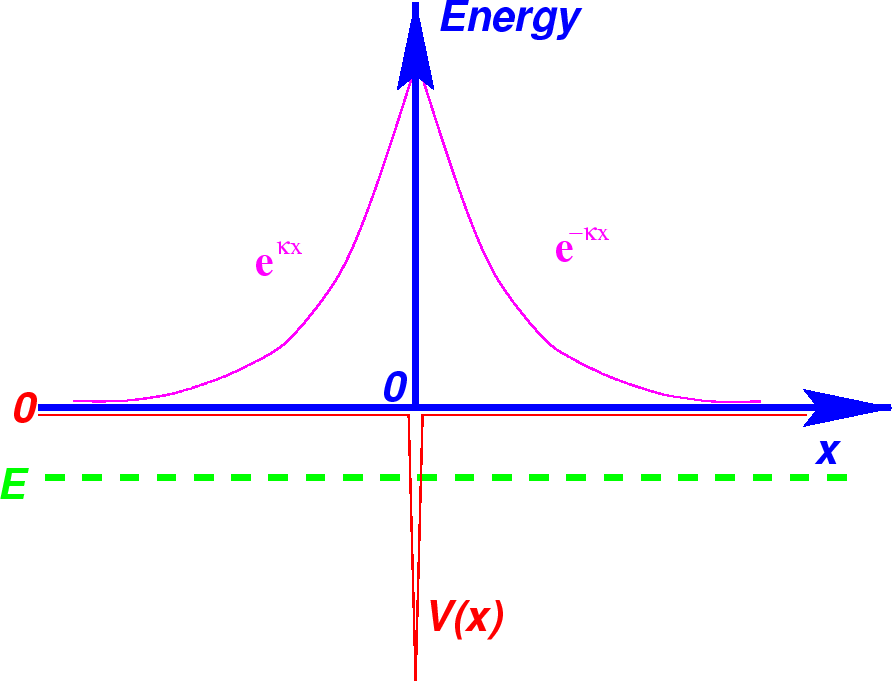
Pegue um potencial de função delta simples e atraente e procure os estados vinculados.
Estes terão energia menor que zero, então as soluções são
Onde
Existem apenas duas regiões, acima e abaixo da função delta. Não precisamos nos preocupar com um ponto em ![]() - as duas soluções corresponderão lá. Já tornamos a função de onda contínua em
- as duas soluções corresponderão lá. Já tornamos a função de onda contínua em ![]() usando o mesmo coeficiente,,
usando o mesmo coeficiente,, ![]() para a solução em ambas as regiões.
para a solução em ambas as regiões.
Agora precisamos encontrar a condição de contorno na primeira derivada em ![]() . Lembre-se de que a função delta causa uma descontinuidade conhecida na primeira derivada.
. Lembre-se de que a função delta causa uma descontinuidade conhecida na primeira derivada.
Colocando a fórmula para ![]() em termos de energia.
em termos de energia.
Existe apenas uma energia para a qual podemos satisfazer as condições de contorno. Existe apenas um estado limitado em um potencial de função delta atraente.
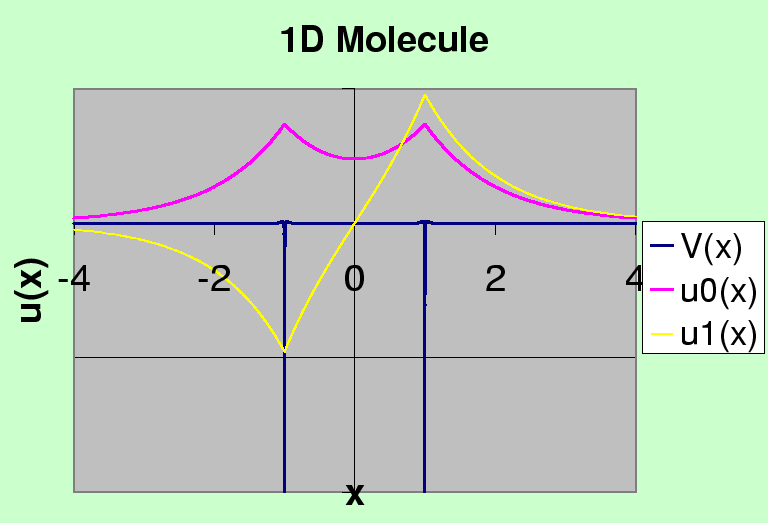
O modelo de função delta de uma molécula
O uso de duas funções delta nos permite ver, até certo ponto, como os átomos se ligam às moléculas . Nosso potencial é
com funções delta atraentes em 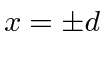 . Este é um potencial simétrico de paridade, então podemos assumir que nossas soluções serão autoestados de paridade.
. Este é um potencial simétrico de paridade, então podemos assumir que nossas soluções serão autoestados de paridade.
Para paridade uniforme, nossa solução nas três regiões é
Uma vez que a solução é projetada para ser simétrica em relação a ![]() , as condições de contorno em
, as condições de contorno em ![]() são as mesmas que em
são as mesmas que em ![]() . As condições de contorno determinam a constante
. As condições de contorno determinam a constante ![]() e restringem
e restringem ![]() .
.
Esta é uma equação transcendental, mas podemos limitar a energia.
Já que para a função delta única, isso é maior do que para a função delta única. Isso significa que é mais negativo e há mais energia de ligação . 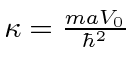
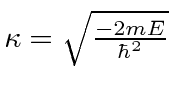
![]()
Basicamente, o elétron não precisa ser localizado com dois átomos como acontece com apenas um. Isso permite que a energia cinética seja menor.
A figura abaixo mostra as duas soluções plotadas no mesmo gráfico do potencial.
Dois átomos de hidrogênio se unem para formar uma molécula com uma separação de 0,74 Angstroms, um pouco maior que o raio de Bohr de 0,53 Angstroms. A energia de ligação (para os dois elétrons) é de cerca de 4,5 eV. Se aproximarmos o potencial de Coulomb com uma função delta, definindo eV Angstroms, nosso cálculo muito ingênuo daria 1,48 eV para um elétron, que é pelo menos da ordem correta de magnitude. 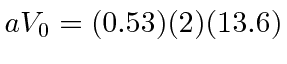
A solução de paridade ímpar tem uma energia que satisfaz a equação
Esta energia é maior do que para uma função delta. Esse estado seria chamado de antiligação .
O modelo de função delta de um cristal
O modelo Kronig-Penny de um cristal sólido contém um conjunto infinito de funções delta repulsivas .
Nossos estados terão energia positiva.
Esse potencial tem uma nova simetria, que uma translação pelo espaçamento da rede![]() deixa o problema inalterado. As distribuições de probabilidade devem, portanto, ter esta simetria
deixa o problema inalterado. As distribuições de probabilidade devem, portanto, ter esta simetria
o que significa que a função de onda difere em uma fase, no máximo.
Combinando as condições de contorno e exigindo que a probabilidade seja periódica, derivamos uma restrição ![]() semelhante às energias quantizadas para estados vinculados.
semelhante às energias quantizadas para estados vinculados.
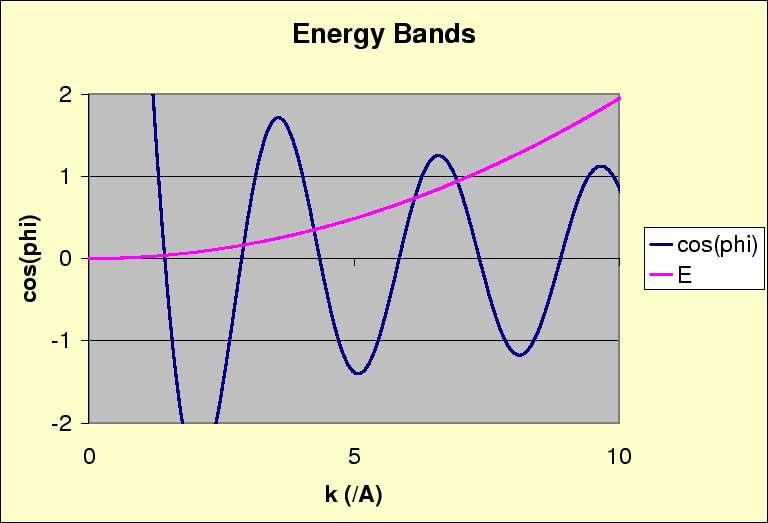
Como 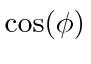 só pode assumir valores entre -1 e 1, são permitidas bandas
só pode assumir valores entre -1 e 1, são permitidas bandas ![]() e intervalos entre essas bandas .
e intervalos entre essas bandas .
O gráfico abaixo é mostrado em função de . Se não estiver entre -1 e 1, não há solução, esse valor de e a energia correspondente não são permitidos. 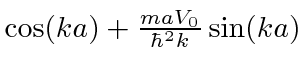
![]()
![]()
Este fenômeno de banda de energia é encontrado em sólidos. Sólidos com faixas parcialmente preenchidas são condutores. Sólidos com faixas preenchidas são isolantes. Os semicondutores têm um pequeno número de portadores de carga (ou orifícios) em uma banda.
A Rotação Quântica
É útil simplesmente investigar o momento angular com apenas um ângulo de rotação livre . Esta pode ser a hélice do plano quântico. Faremos um bom trabalho nisso em 3 dimensões mais tarde.
Vamos supor que temos uma massa ![]() restrita a se mover em um círculo de raio
restrita a se mover em um círculo de raio![]() . Suponha que o movimento no círculo seja livre, então não há potencial. A energia cinética é
. Suponha que o movimento no círculo seja livre, então não há potencial. A energia cinética é
Se medirmos a distância ao redor do círculo, 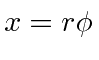 o único problema que temos é que, uma vez que eu dê a volta completa no círculo, estou de volta
o único problema que temos é que, uma vez que eu dê a volta completa no círculo, estou de volta ![]() . Vamos seguir em frente e escrever nossa função de onda.
. Vamos seguir em frente e escrever nossa função de onda.
Lembrando o momento angular, vamos chamar a combinação 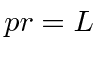 . Nossa onda é .
. Nossa onda é .
Deve ser de valor único, então precisamos exigir que
O momento angular deve ser quantizado em unidades de![]() .
.
Isso também será verdade para as 3 dimensões; no entanto, os 3 componentes do momento angular não comutam entre si, levando a todos os tipos de diversão.
Derivações e cálculos
Fluxo de probabilidade para a etapa potencial
O fluxo de probabilidade é dado por
Podemos economizar algum esforço observando que ele contém uma expressão sem seu conjugado complexo. (Isso garante que o termo entre colchetes seja imaginário e o fluxo seja real.)
A probabilidade de ser refletido é o fluxo refletido dividido pelo fluxo incidente. Neste caso é fácil perceber que é 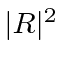 como dissemos. Para
como dissemos. Para 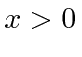
A probabilidade de ser transmitido é o fluxo transmitido dividido pelo fluxo incidente.
novamente como havíamos calculado antes.
Dispersão de um Poço Potencial 1D
Numerando as três regiões da esquerda para a direita,
Novamente, não assumimos nenhum incidente de onda da direita (mas poderíamos adicionar essa solução se quiséssemos).
Agora combinamos a função de onda e sua primeira derivada nos dois limites, resultando em 4 equações. Isso é bom, pois temos 4 constantes para determinar. Em ![]() temos 2 equações que podemos usar para eliminar
temos 2 equações que podemos usar para eliminar ![]() e
e ![]() .
.
Em 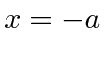 temos 2 equações que agora podem ser escritas em termos de
temos 2 equações que agora podem ser escritas em termos de ![]() e
e ![]() usando o acima.
usando o acima.
Podemos adicionar equações para eliminar ![]() .
.
Podemos subtrair as mesmas equações para resolvê-las com mais facilidade ![]() .
.
Resolvemos as equações das condições de contorno para encontrar as amplitudes de reflexão e transmissão
Os quadrados destes fornecem a probabilidade de reflexão e transmissão, uma vez que o potencial é o mesmo nas duas regiões.
Estados vinculados de um poço potencial 1D
Nas duas regiões externas, temos soluções
No centro, temos a mesma solução de antes.
(Observe que mudamos de ![]() para
para ![]() para economia.) Teremos 4 equações em 4 coeficientes desconhecidos.
para economia.) Teremos 4 equações em 4 coeficientes desconhecidos.
Resolvendo a Equação Diferencial OH
A equação diferencial para o oscilador harmônico 1D é.
Ao trabalhar com variáveis e constantes adimensionais, podemos ver a equação básica e minimizar a desordem. Usamos a energia em termos de ![]() .
.
Definimos uma coordenada adimensional.
A equação se torna.
(É provavelmente mais fácil apenas verificar a equação acima substituindo como abaixo.
Funciona.)
Agora queremos encontrar a solução para . 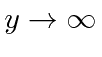
torna-se
que tem a solução (no ![]() limite grande )
limite grande )
Este exponencial irá dominar um polinômio para que possamos escrever nossa solução geral como 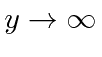
Pegue a equação diferencial
e plugue
para conseguir
Esta é nossa equação diferencial para o polinômio 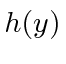 .
.
Escreva 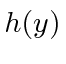 como uma soma de termos.
como uma soma de termos.
Conecte-o à equação diferencial.
Agora queremos mudar os termos na soma de modo que vejamos o coeficiente de ![]() . Para fazer isso, vamos deslocar o termo duas etapas para baixo na soma. Agora aparecerá como .
. Para fazer isso, vamos deslocar o termo duas etapas para baixo na soma. Agora aparecerá como . 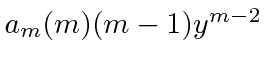
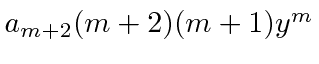
(Observe que, ao fazer essa mudança, o primeiro termo para ![]() e para
e para ![]() é deslocado da soma. Isso está OK, pois é zero para ou .)
é deslocado da soma. Isso está OK, pois é zero para ou .) 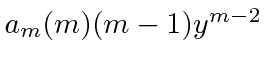
![]()
![]()
Para que a soma seja zero para todos ![]() , cada coeficiente de
, cada coeficiente de ![]() deve ser zero.
deve ser zero.
e temos uma relação de recursão nos dando nosso polinômio.
Mas, vamos ver o que temos. Para grande ![]() ,
,
A série para
tem o coeficiente 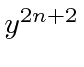 igual a e o coeficiente igual a . Se ,
igual a e o coeficiente igual a . Se , 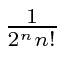
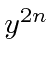
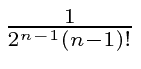
![]()
Portanto, nossa solução polinomial se aproximará 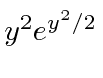 e nossa solução geral não será normalizável. (Lembre-se .) Devemos evitar isso.
e nossa solução geral não será normalizável. (Lembre-se .) Devemos evitar isso. 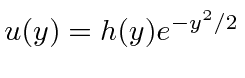
Podemos evitar o problema se a série terminar e não for infinita ![]() .
.
A série terminará se
por algum valor de ![]() . Então, o último termo da série estará em ordem
. Então, o último termo da série estará em ordem ![]() .
.
As soluções aceitáveis, então, satisfazem o requisito
Novamente, obtemos energias quantizadas quando satisfazemos as condições de contorno no infinito.
A função de onda do estado fundamental é particularmente simples, tendo apenas um termo.
Vamos encontrar ![]() normalizando a função de onda.
normalizando a função de onda.
Modelo 1D de uma derivação de molécula
Uma vez que a solução é projetada para ser simétrica em relação a ![]() , as condições de contorno em
, as condições de contorno em ![]() são as mesmas que em
são as mesmas que em ![]() . As condições de contorno determinam a constante
. As condições de contorno determinam a constante ![]() e restringem
e restringem ![]() .
.
A descontinuidade na primeira derivada de ![]() at
at ![]() é
é
Precisamos estudar esta equação transcendental para ver quais são as energias permitidas.
Modelo 1D de uma derivação de cristal
Estamos trabalhando com o potencial periódico
Nossos estados têm energia positiva. Esse potencial tem a simetria de que uma translação pelo espaçamento da rede ![]() deixa o problema inalterado. As distribuições de probabilidade devem, portanto, ter esta simetria
deixa o problema inalterado. As distribuições de probabilidade devem, portanto, ter esta simetria
o que significa que a função de onda difere em uma fase, no máximo.
Agora, vamos examinar as condições de contorno em ![]() . A continuidade da função de onda dá
. A continuidade da função de onda dá
A descontinuidade na primeira derivada é
Substituindo 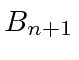 da primeira equação
da primeira equação
Conectando esta equação de 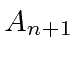 volta à equação acima para
volta à equação acima para 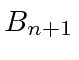 obtermos
obtermos
Agora temos dois pares de equações para os 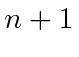 coeficientes em termos dos
coeficientes em termos dos ![]() coeficientes.
coeficientes.
Usando o segundo par de equações para eliminar os 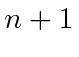 coeficientes, temos
coeficientes, temos
Agora podemos eliminar todos os coeficientes.
Essa relação impõe restrições ![]() , como as restrições que nos fornecem energias quantizadas para estados vinculados. Como
, como as restrições que nos fornecem energias quantizadas para estados vinculados. Como 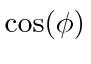 só pode assumir valores entre -1 e 1, são permitidas bandas
só pode assumir valores entre -1 e 1, são permitidas bandas ![]() e intervalos entre essas bandas.
e intervalos entre essas bandas.
Exemplos
Toda esta seção é de exemplos
Problemas de teste de amostra
- Um feixe de elétrons de 100 eV (energia cinética) incide sobre um degrau potencial de altura
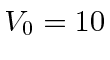 eV. Calcule a probabilidade de ser transmitido. Obtenha uma resposta numérica.
eV. Calcule a probabilidade de ser transmitido. Obtenha uma resposta numérica. - * Encontre os estados próprios de energia (e valores próprios de energia) de uma partícula de massa
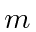 ligada ao potencial 1D. Suponha queseja um número real positivo. (Não presuma quetem unidades de energia.) Você não precisa normalizar o estado. Responder
ligada ao potencial 1D. Suponha queseja um número real positivo. (Não presuma quetem unidades de energia.) Você não precisa normalizar o estado. Responder 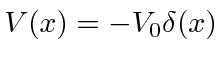
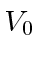
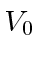
- * Um feixe de partículas de número de onda
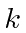 (isto significa
(isto significa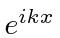 ) incide sobre um potencial unidimensional. Calcule a probabilidade de ser transmitido. Represente graficamente como uma função de. Resposta À esquerda da origem está a solução. À direita da origem está a solução. Continuidade dena origem implica. A descontinuidade na primeira derivada é
) incide sobre um potencial unidimensional. Calcule a probabilidade de ser transmitido. Represente graficamente como uma função de. Resposta À esquerda da origem está a solução. À direita da origem está a solução. Continuidade dena origem implica. A descontinuidade na primeira derivada é 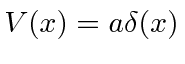
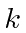
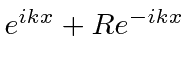
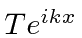
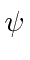
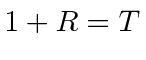
A probabilidade de transmissão começa em zero para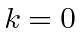 então se aproxima
então se aproxima 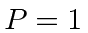 assintoticamente para .
assintoticamente para . 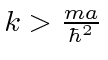
- * Um feixe de partículas de energia que
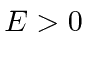 vem
vem incide sobre um potencial de função delta em uma dimensão. Isso é.
incide sobre um potencial de função delta em uma dimensão. Isso é. 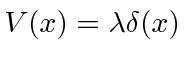
- a)
- Encontre a solução para a equação de Schrödinger para este problema.
- b)
- Determine os coeficientes necessários para satisfazer as condições de contorno.
- c)
- Calcule a probabilidade de uma partícula no feixe ser refletida pelo potencial e a probabilidade de ser transmitida.
- * A equação de Schrödinger para o ocilador harmônico unidimensional é reduzida à seguinte equação para o polinômio
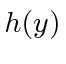 :
:
- Um feixe de partículas de energia que
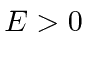 vem
vem 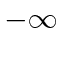 incide sobre uma etapa potencial em uma dimensão. Isso é
incide sobre uma etapa potencial em uma dimensão. Isso é 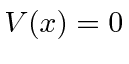 para
para 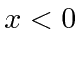 e
e 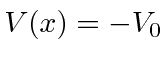 para
para 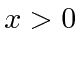 onde
onde 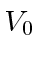 está um número real positivo.
está um número real positivo.
- a)
- Encontre a solução para a equação de Schrödinger para este problema.
- b)
- Determine os coeficientes necessários para satisfazer as condições de contorno.
- c)
- Calcule a probabilidade de uma partícula no feixe ser refletida pelo passo potencial e a probabilidade de ser transmitida.
- * Uma partícula está no estado fundamental (.) De um potencial oscilador harmônico. De repente, o potencial é removido sem afetar o estado da partícula. Encontre a distribuição de probabilidadepara o momento da partícula depois que o potencial foi removido.
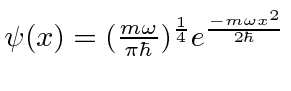
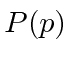
- * Uma partícula está no terceiro estado excitado (n = 3) do potencial oscilador harmônico unidimensional.
- a)
- Calcule essa autofunção de energia, até um fator de normalização, a partir das relações de recursão fornecidas na parte frontal do exame.
- b)
- Dê, mas não avalie, a expressão para o fator de normalização.
- c)
- No
 potencial é subitamente removido para que a partícula fique livre. Suponha que a função de onda da partícula não seja alterada pela remoção do potencial. Escreva uma expressão para a probabilidade de que a partícula tenha momento no intervalo
potencial é subitamente removido para que a partícula fique livre. Suponha que a função de onda da partícula não seja alterada pela remoção do potencial. Escreva uma expressão para a probabilidade de que a partícula tenha momento no intervalo 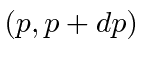 de
de 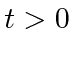 . Você não precisa avaliar a integral.
. Você não precisa avaliar a integral.
- * A equação de Schrödinger para o oscilador harmônico unidimensional é reduzida à seguinte equação para o polinômio
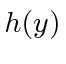 :
:
- * Encontre os estados próprios de energia (e valores próprios de energia) de uma partícula de massa
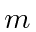 ligada ao potencial 1D.
ligada ao potencial 1D. 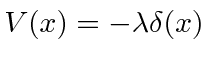
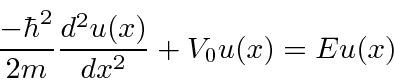
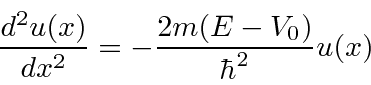
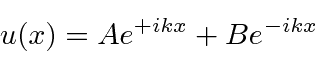
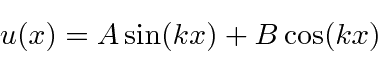
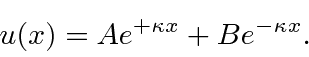
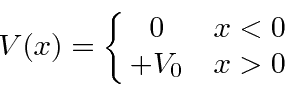
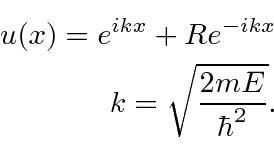
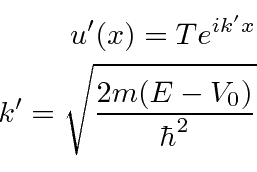
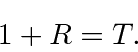
![\ begin {displaymath} \ bgroup \ color {black} [ike ^ {ikx} -ikRe ^ {- ikx}] _ {x = 0} = [ik'Te ^ {ik'x}] _ {x = 0} \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1232.png)
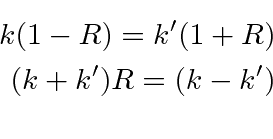
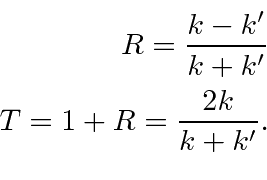
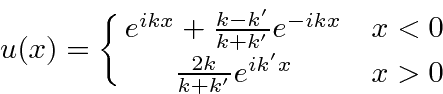
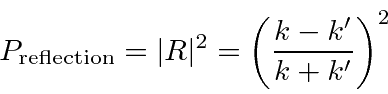
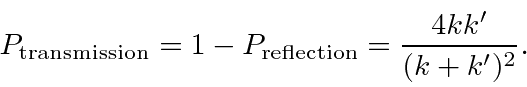
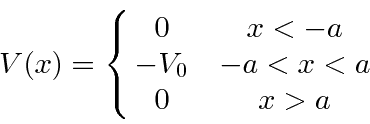
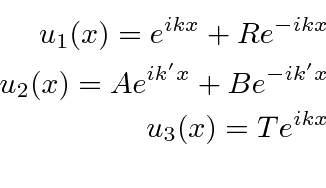
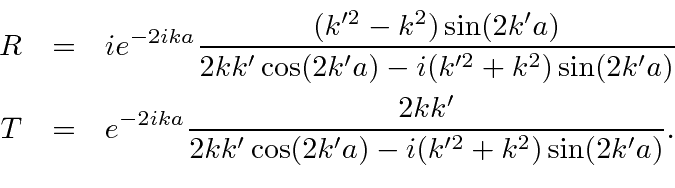
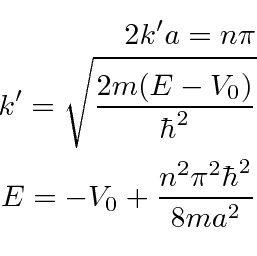

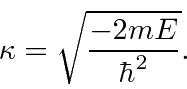
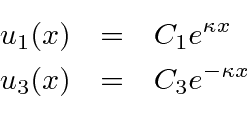
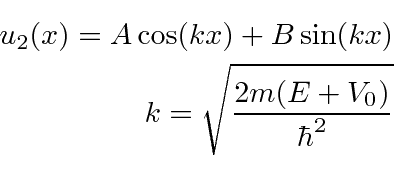
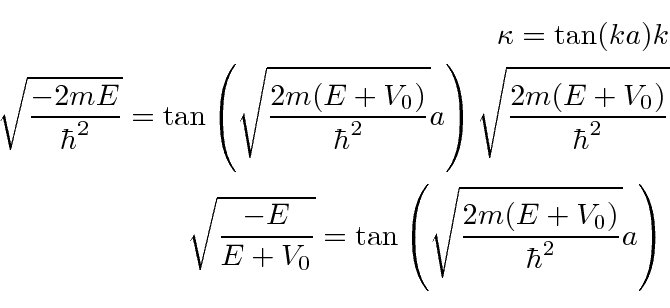
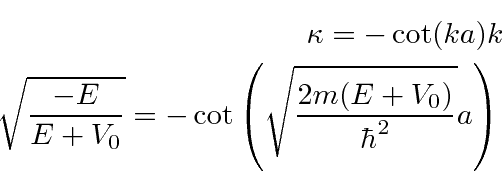
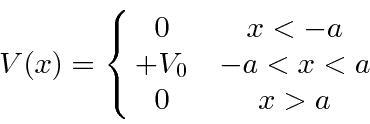
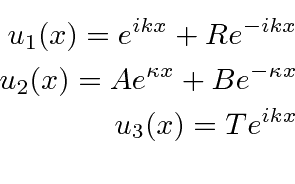
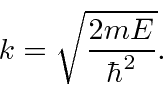
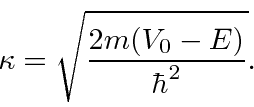
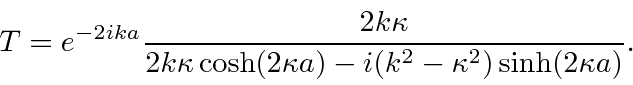
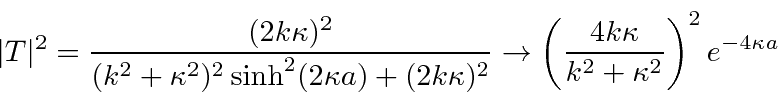
![\ begin {displaymath} \ bgroup \ color {black} \ vert T \ vert ^ 2 \ approx e ^ {- 2 \ kappa (2a)} = e ^ {- 2 \ int \ limits _ {- a} ^ a \ sqrt {{2m \ over \ hbar ^ 2} [V (x) -E]}} dx \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1266.png)
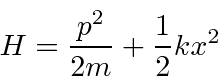
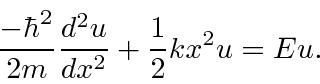
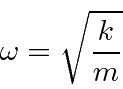
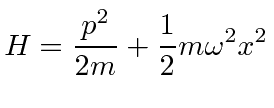
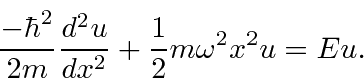
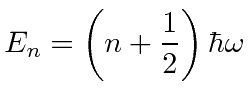
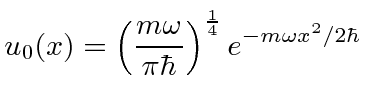
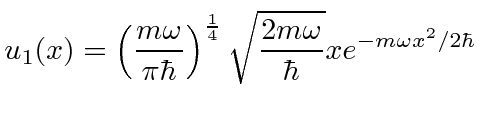
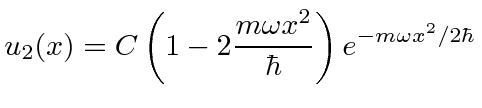
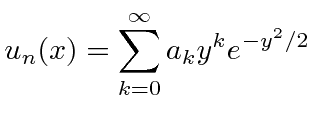
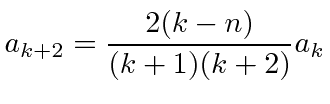
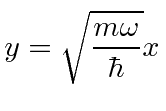
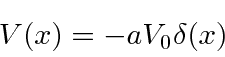
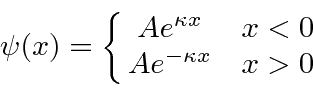
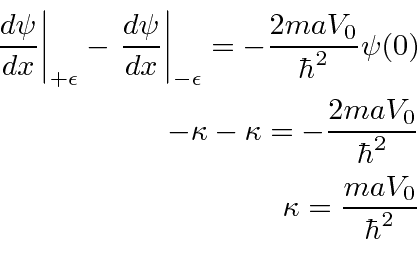
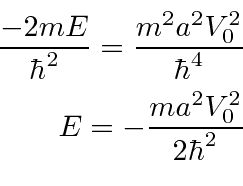
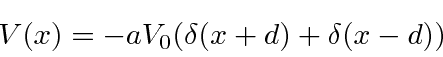
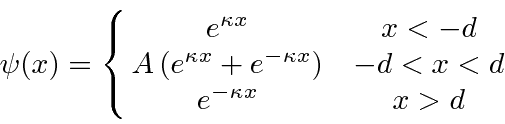
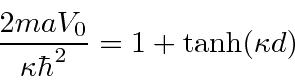
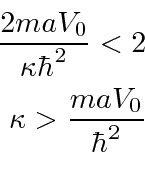
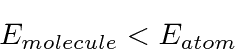
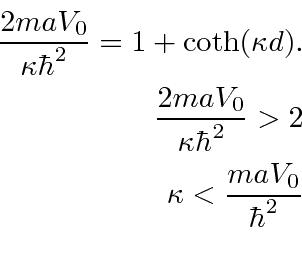
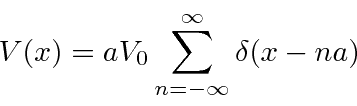
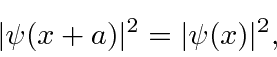
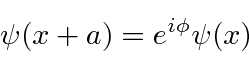
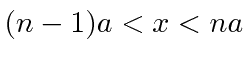
![\ begin {displaymath} \ bgroup \ color {black} \ psi_n (x) = A_n \ sin (k [x-na]) + B_n \ cos (k [x-na]) \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1303.png)
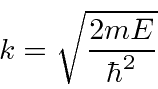
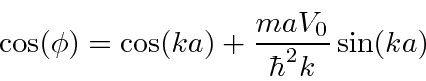
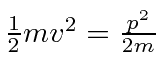
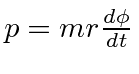
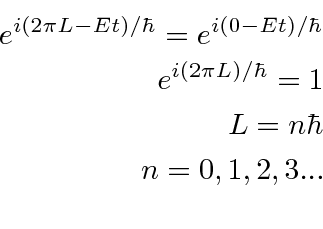
![\ begin {displaymath} \ bgroup \ color {black} j (x, t) = {\ hbar \ over 2mi} \ left [\ psi ^ * {\ pa ... ... \ partial x} - {\ partial \ psi ^ * \ over \ partial x} \ psi \ right]. \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1319.png)
![\ begin {displaymath} \ bgroup \ color {black} j = {\ hbar \ over 2im} \ left [u ^ * {du \ over dx} -... ... \ right] = {\ hbar \ over 2im } \ left [u ^ * {du \ over dx} -CC \ right] \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1320.png)
![\ begin {eqnarray *} j & = & {\ hbar \ over 2im} [(e ^ {- ikx} + R ^ * e ^ {ikx}) (ike ^ {ikx} -ikRe ^ {- ik .... ..2ikx} -R ^ * R] + CC \\ j & = & [1- \ vert R \ vert ^ 2] {\ hbar k \ over m}. \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1321.png)
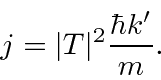
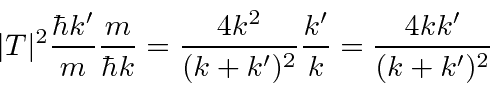
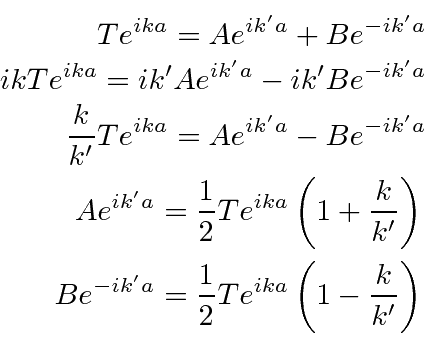
![\ begin {eqnarray *} e ^ {- ika} + Re ^ {ika} = Ae ^ {- ik'a} + Be ^ {ik'a} \\ ike ^ {- ika} -ikRe ^ {ik .. . ... \ direita) e ^ {- 2ik'a} - \ esquerda ({k '\ sobre k} -1 \ direita) e ^ {2ik'a} \ direita] \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1327.png)
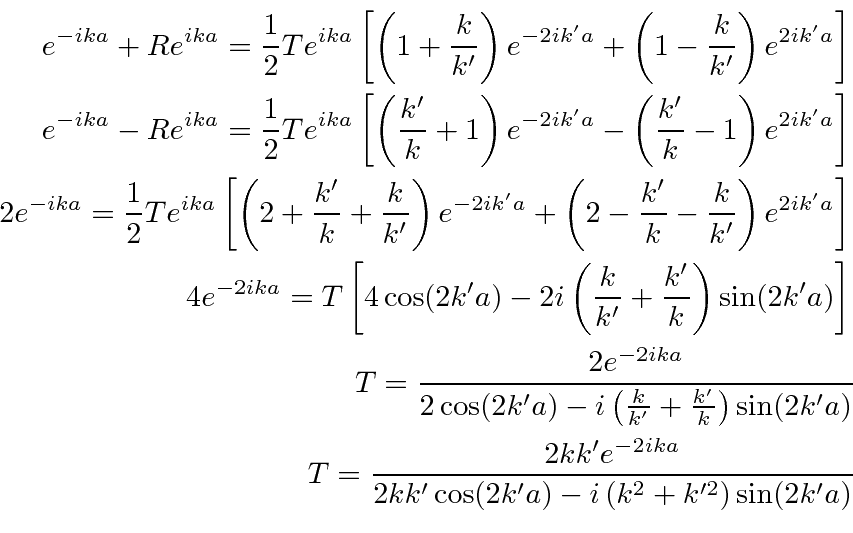
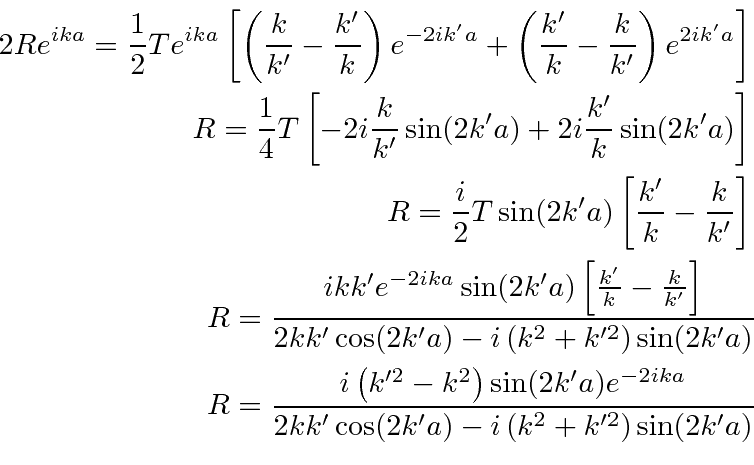
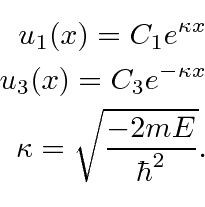
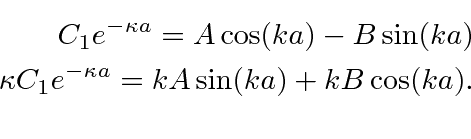
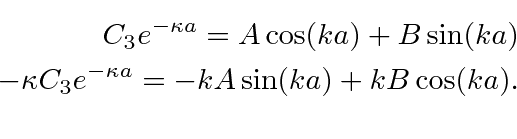
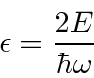
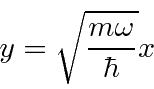
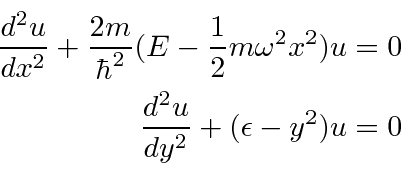
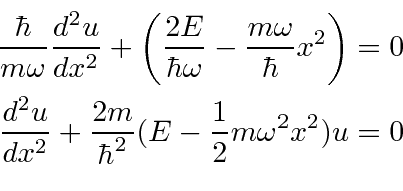
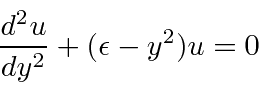
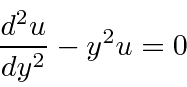
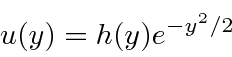
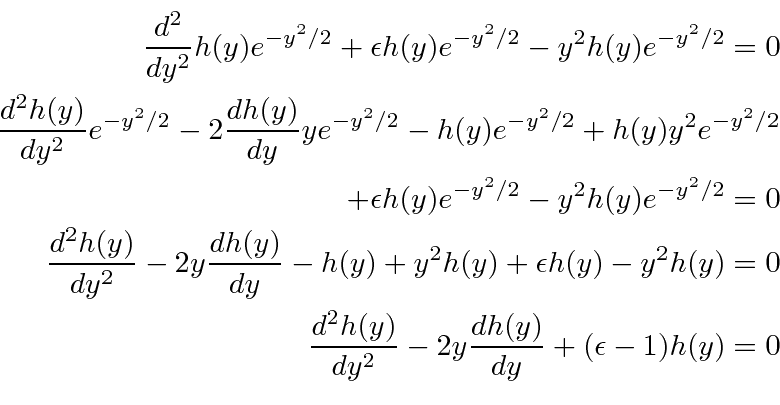
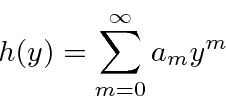
![\ begin {displaymath} \ bgroup \ color {black} \ sum \ limits_ {m = 0} ^ \ infty [a_m (m) (m-1) y ^ {m-2} -2a_m (m) y ^ m + ( \ epsilon-1) a_my ^ m] = 0 \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1355.png)
![\ begin {displaymath} \ bgroup \ color {black} \ sum \ limits_ {m = 0} ^ \ infty [a_ {m + 2} (m + 2) (m + 1) -2a_m (m) + (\ epsilon -1) a_m] y ^ m = 0 \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1359.png)
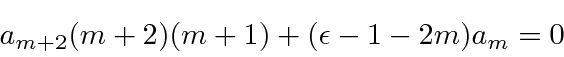
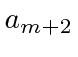
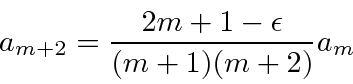
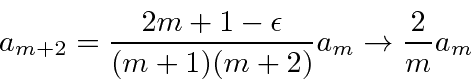
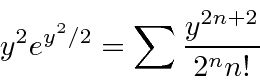
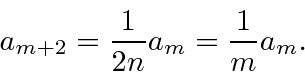
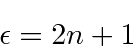
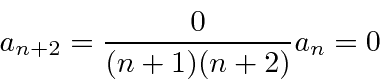
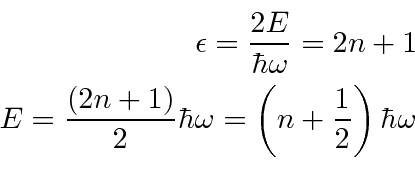
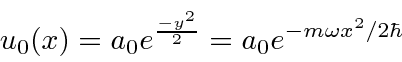
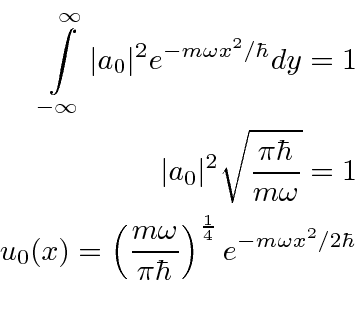
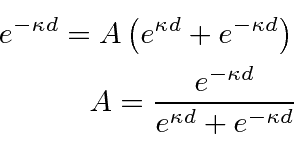
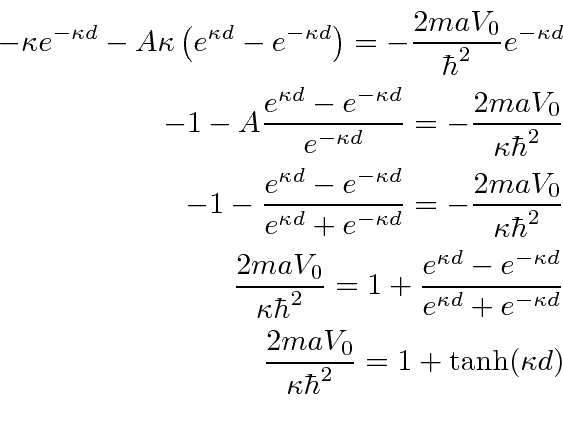
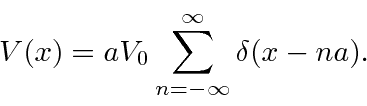
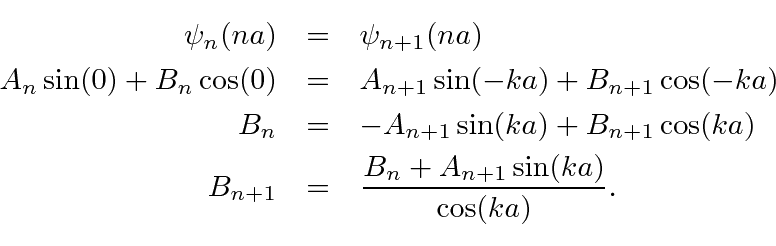
![\ begin {eqnarray *} \ left. {d \ psi_ {n + 1} \ over dx} \ right \ vert _ {na} - \ left. {d \ psi_ {n ... ... A_ {n + 1} \ cos (ka) + B_ {n + 1} \ sin (ka) -A_n] = {2maV_0 \ over \ hbar ^ 2} B_n \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1387.png)
![\ begin {eqnarray *} k [A_ {n + 1} \ cos (ka) + [B_n + A_ {n + 1} \ sin (ka)] \ tan (ka) -A_n] = {2maV_0 \ o .. . ... + 1} = {2maV_0 \ over \ hbar ^ 2k} B_n \ cos (ka) -B_n \ sin (ka) + A_n \ cos (ka) \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1389.png)