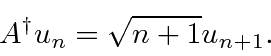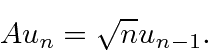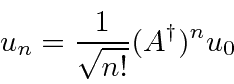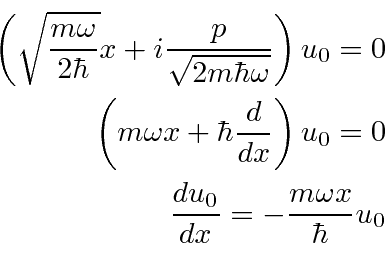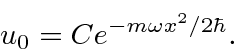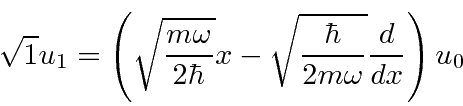Os métodos do operador são muito úteis para resolver o problema do oscilador harmônico e para qualquer tipo de cálculo do potencial HO. Os operadores que desenvolvemos também serão úteis na quantização do campo eletromagnético.
O Hamiltoniano para o Oscilador Harmônico 1D
parece que pode ser escrito como o quadrado de um operador. Pode ser reescrito em termos do operador ![]()
Usaremos os comutadores entre ![]() ,
, ![]() e
e ![]() para resolver o problema HO.
para resolver o problema HO.
Os comutadores com o hamiltoniano são facilmente calculados.
A partir desses comutadores, podemos mostrar que ![]() é um operador de aumento para os estados do oscilador harmônico
é um operador de aumento para os estados do oscilador harmônico
e esse ![]() é um operador de rebaixamento .
é um operador de rebaixamento .
Como a redução deve parar em um estado fundamental com energia positiva, podemos mostrar que as energias permitidas são
As funções de onda reais podem ser deduzidas usando os operadores diferenciais para ![]() e
e ![]() , mas geralmente é mais útil definir o
, mas geralmente é mais útil definir o ![]() estado próprio em termos do estado fundamental e dos operadores de elevação.
estado próprio em termos do estado fundamental e dos operadores de elevação.
Quase qualquer cálculo de interesse pode ser feito sem funções reais, uma vez que podemos expressar os operadores para posição e momento.
Apresentando 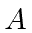 e
e 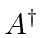
O Hamiltoniano para o Oscilador Harmônico 1D
pode ser reescrito em termos do operador
e seu conjugado hermitiano
Ambos os termos no hamiltoniano do oscilador harmônico são quadrados de operadores. Observe que ![]() é escolhido de forma que
é escolhido de forma que ![]() seja próximo ao hamiltoniano. Primeiro, calcule a quantidade
seja próximo ao hamiltoniano. Primeiro, calcule a quantidade
A partir disso, podemos ver que o hamiltoniano pode ser escrito em termos de
Comutadores de 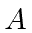 ,
, 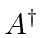 e
e 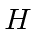
Usaremos o comutador entre ![]() e
e ![]() para resolver o problema OH. Os operadores são definidos para serem
para resolver o problema OH. Os operadores são definidos para serem
O comutador é
Vamos usar este comutador simples
para calcular comutadores com o Hamiltoniano . Isso é fácil se
Use comutadores para derivar energias HO
Nós calculamos os comutadores
Aplique ![\ bgroup \ color {black} $ [H, A] $ \ egroup](https://quantummechanics.ucsd.edu/ph130a/130_notes/img182.png) à autofunção de energia
à autofunção de energia ![]() .
.
Esta equação mostra que
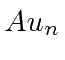 é uma autofunção de
é uma autofunção de 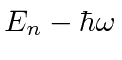
Agora, aplique ![\ bgroup \ color {black} $ [H, A ^ \ dagger] $ \ egroup](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1447.png) à autofunção de energia
à autofunção de energia ![]() .
.
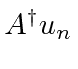 é uma autofunção de
é uma autofunção de 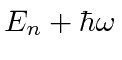
Não podemos continuar reduzindo a energia porque a energia HO não pode cair abaixo de zero .
A única maneira de impedir que o operador de abaixamento tire a energia negativa é que o abaixamento forneça zero para a função de onda. Como será o nível de energia mais baixo, isso deve acontecer para o estado fundamental. Quando diminuímos o estado fundamental, devemos obter zero .
Como o hamiltoniano contém
A energia do estado fundamental é e os estados em geral têm energias
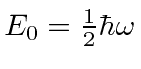
uma vez que mostramos o aumento e a redução em etapas de
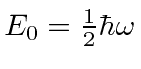
É interessante notar que temos um operador de número para ![]()
Aumentando e diminuindo constantes
Sabemos que aumenta a energia de um estado próprio, mas não sabemos que coeficiente ele produz diante do novo estado. ![]()
Podemos calcular o coeficiente usando nossos operadores.
O efeito do operador de levantamento é
Da mesma forma, o efeito do operador de redução é
Essas são equações extremamente importantes para qualquer cálculo no problema HO.
Também podemos escrever qualquer autoestado de energia em termos do estado fundamental e do operador de aumento .
Valores de expectativa de 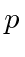 e
e 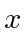
É importante perceber que podemos apenas usar a definição de ![]() escrever
escrever ![]() e
e ![]() em termos dos operadores de subida e descida.
em termos dos operadores de subida e descida.
Isso permitirá qualquer cálculo.
* Exemplo: O valor esperado de ![]() para qualquer autoestado de energia é zero. *
para qualquer autoestado de energia é zero. *
* Exemplo: O valor esperado de ![]() para qualquer autoestado de energia é zero. *
para qualquer autoestado de energia é zero. *
* Exemplo: O valor esperado de ![]() no estado .
no estado . 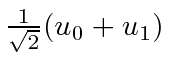 *
*
* Exemplo: O valor esperado de para qualquer autoestado de energia é . 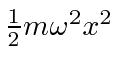
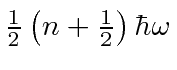 *
*
* Exemplo: O valor esperado de 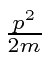 para qualquer autoestado de energia é .
para qualquer autoestado de energia é . 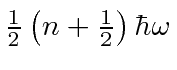 *
*
* Exemplo: O valor esperado de ![]() em função do tempo para o estado
em função do tempo para o estado 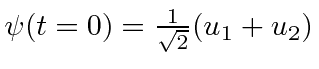 é .
é . 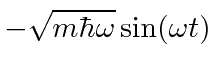 *
*
A função de onda para o estado fundamental HO
A equação
pode ser usado para encontrar a função de onda do estado fundamental . Escreva
Esta equação diferencial de primeira ordem pode ser resolvida para obter a função de onda.
Poderíamos continuar com o operador de levantamento para obter estados animados.
Normalmente, não precisaremos das funções de onda reais para nossos cálculos.
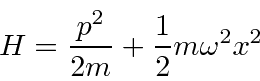
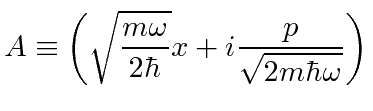
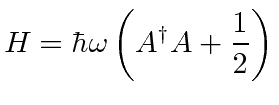
![\ bgroup \ color {black} $ \ displaystyle [A, A ^ \ dagger] = 1 $ \ egroup](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1428.png)
![\ begin {eqnarray *} [H, A] & = & - \ hbar \ omega A \\ {[H, A ^ \ dagger]} & = & \ hbar \ omega A ^ \ dagger \\ \ end {eqnarray * }](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1429.png)
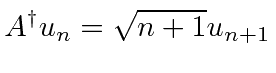
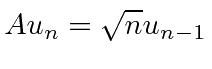
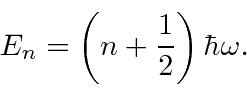
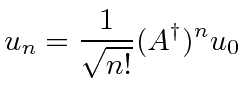
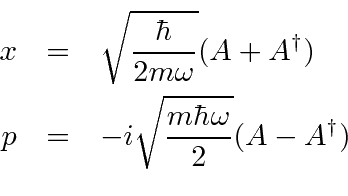
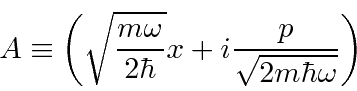
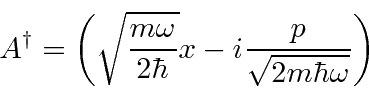
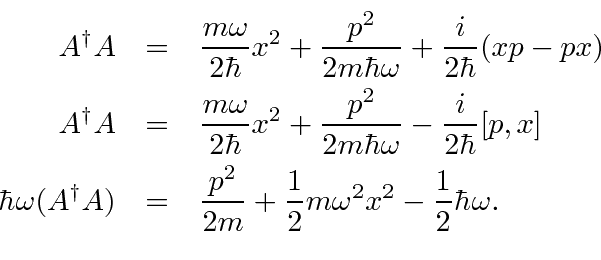
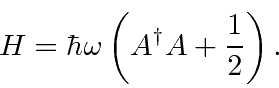
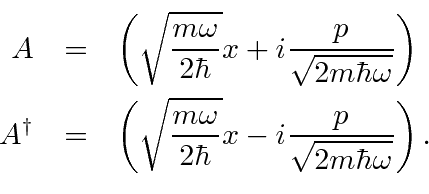
![\ begin {eqnarray *} [A, A ^ \ dagger] & = & {m \ omega \ over2 \ hbar} [x, x] + {1 \ over 2m \ hbar \ omega ... ... \\ & = & {i \ over 2 \ hbar} (- [x, p] + [p, x]) = {i \ over \ hbar} [p, x] = 1. \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1441.png)
![\ begin {displaymath} \ bgroup \ color {black} [A, A ^ \ dagger] = 1 \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1442.png)
![\ begin {eqnarray *} [H, A] & = & \ hbar \ omega [A ^ \ dagger A, A] = \ hbar \ omega [A ^ \ dagger, A] A = - \ ... ... er] = \ hbar \ omega A ^ \ dagger [A, A ^ \ dagger] = \ hbar \ omega A ^ \ dagger \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1443.png)
![\ begin {eqnarray *} [H, A] u_n = - \ hbar \ omega Au_n \\ HAu_n-AHu_n = - \ hbar \ omega Au_n \\ ... ... (Au_n) = - \ hbar \ omega Au_n \ \ H (Au_n) = (E_n- \ hbar \ omega) (Au_n) \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1444.png)
![\ begin {eqnarray *} [H, A ^ \ dagger] u_n = \ hbar \ omega A ^ \ dagger u_n \\ HA ^ \ dagger u_n-A ... ... r u_n) \\ H (A ^ \ punhal u_n) = (E_n + \ hbar \ omega) (A ^ \ punhal u_n) \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1448.png)
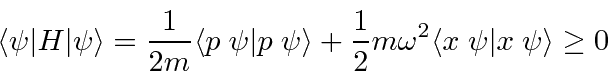
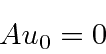
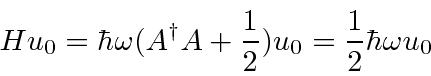
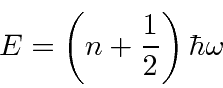
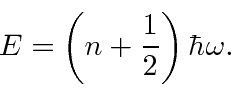
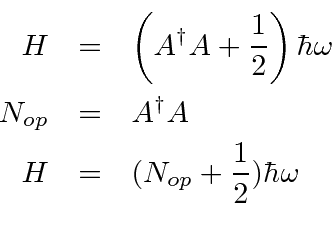
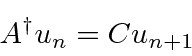
![\ begin {eqnarray *} \ vert C \ vert ^ 2 & = & \ langle A ^ \ punhal u_n \ vert A ^ \ punhal u_n \ ran ... ...]) u_n \ vert u_n \ rangle = (n + 1) \ langle u_n \ vert u_n \ rangle = n + 1 \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1458.png)