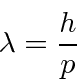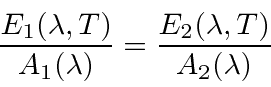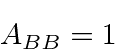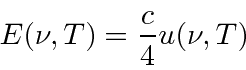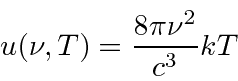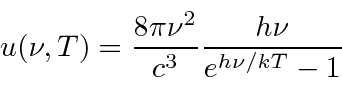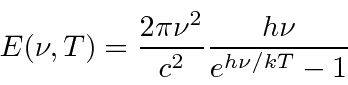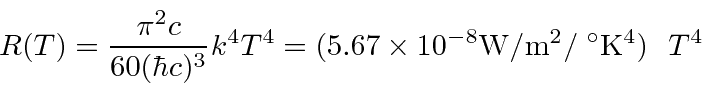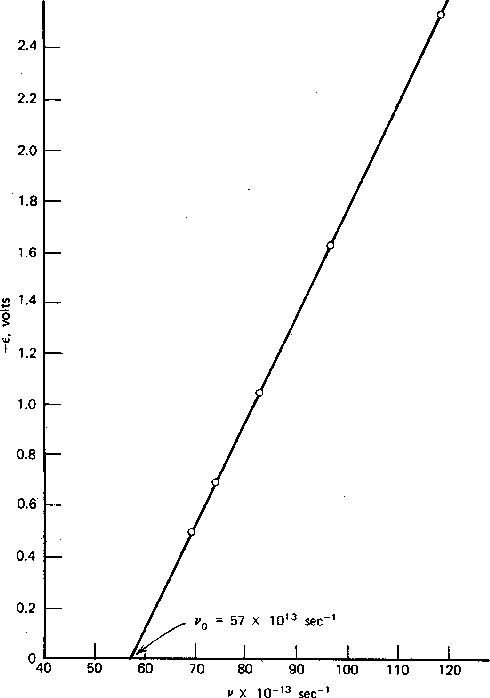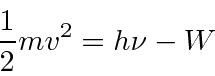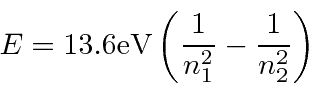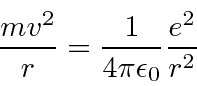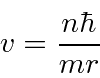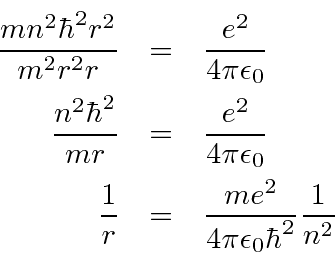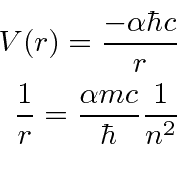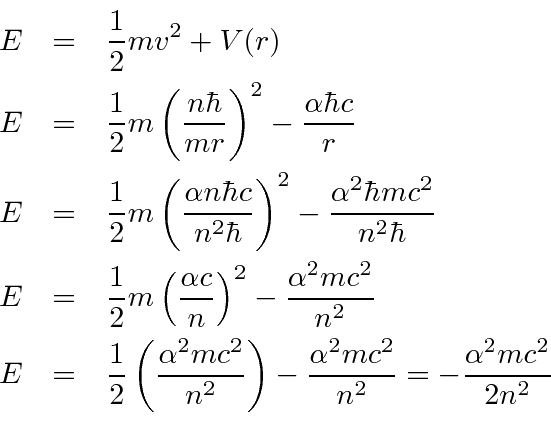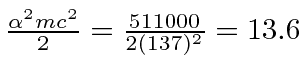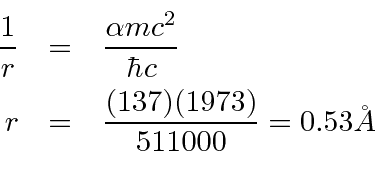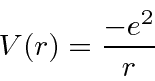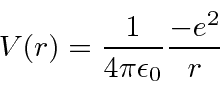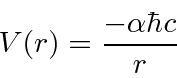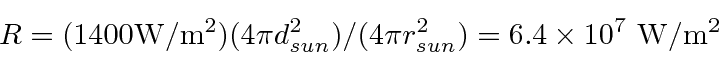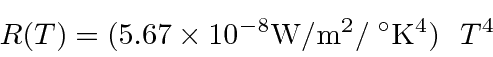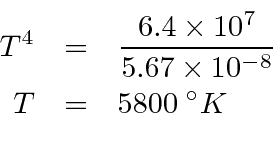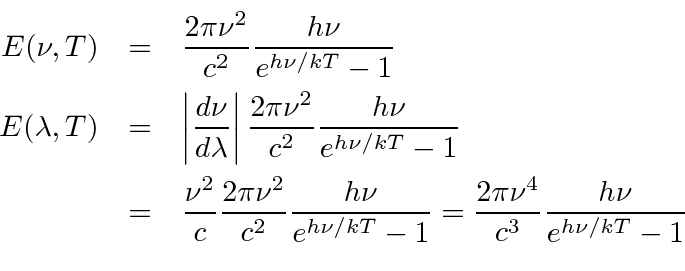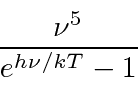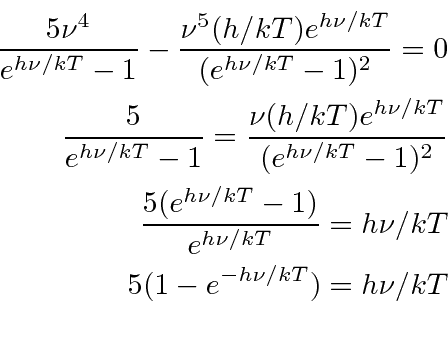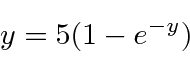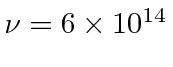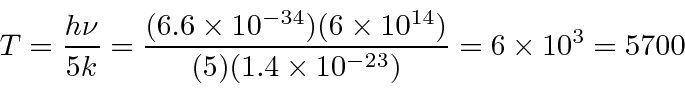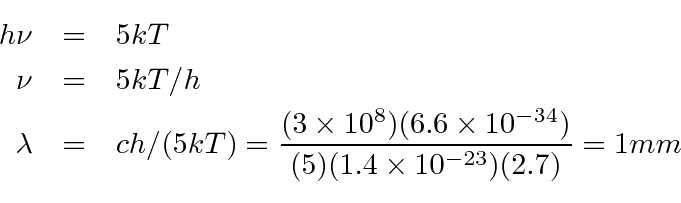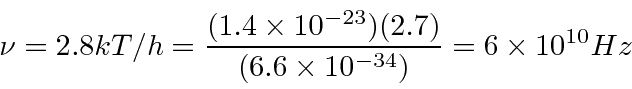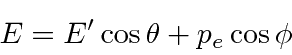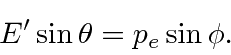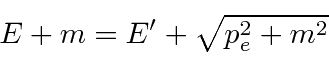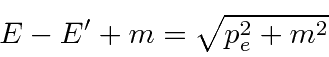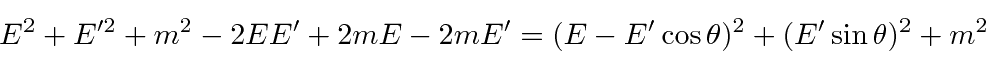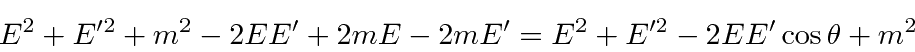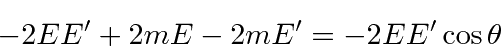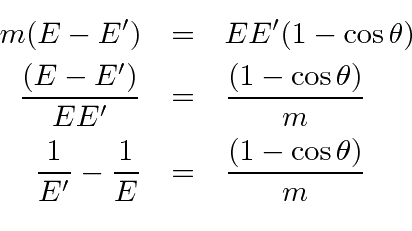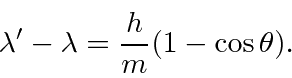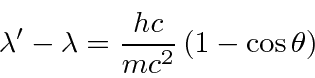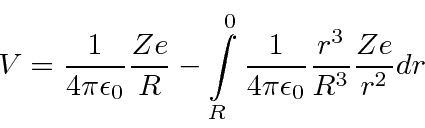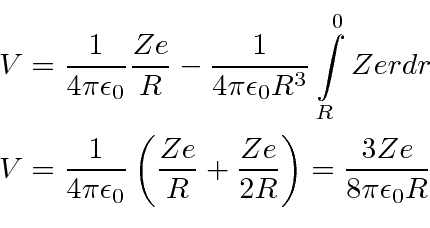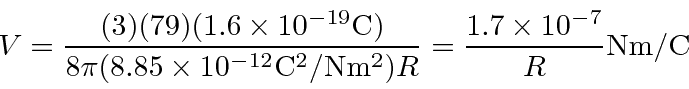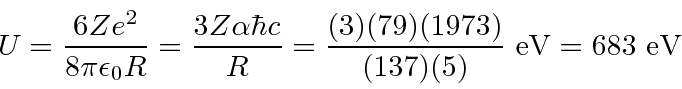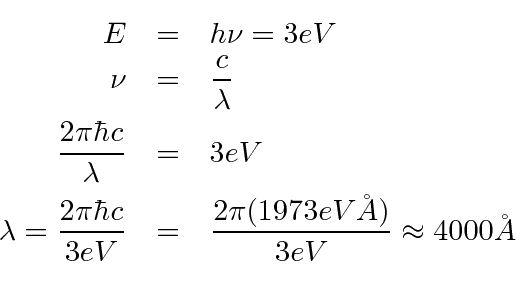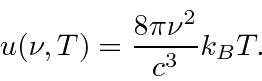No final do século XIX, as leis da física baseavam-se na mecânica e na lei da gravitação de Newton, nas equações de Maxwell que descreviam a eletricidade e o magnetismo e na mecânica estatística que descrevia o estado de uma grande coleção de matéria. Essas leis da física descreveram a natureza muito bem na maioria das condições, no entanto, algumas medições do final do século 19 e início do século 20 não puderam ser compreendidas. Os problemas com a física clássica levaram ao desenvolvimento da Mecânica Quântica e da Relatividade Especial.
Alguns dos problemas que levaram ao desenvolvimento da Mecânica Quântica estão listados aqui.
- Radiação de corpo negro: a física clássica previu que objetos quentes irradiariam instantaneamente todo o seu calor em ondas eletromagnéticas. O cálculo, que foi baseado nas equações de Maxwell e na Mecânica Estatística, mostrou que a taxa de radiação foi para o infinito quando o comprimento de onda EM foi para zero, "A Catástrofe Ultravioleta". Plank resolveu o problema postulando que a energia EM foi emitida em quanta com
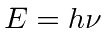 .
. - O efeito fotoelétrico: quando a luz foi usada para tirar os elétrons dos sólidos, os resultados foram completamente diferentes do que se esperava das equações de Maxwell. As medições eram fáceis de explicar (para Einstein) se a luz fosse composta de partículas com as energias postuladas por Plank.
- Átomos: Depois que Rutherford descobriu que a carga positiva nos átomos estava concentrada em um núcleo muito pequeno, a física clássica previu que os elétrons atômicos orbitando o núcleo irradiariam sua energia e entrariam em espiral no núcleo. Isso claramente não aconteceu. A energia irradiada pelos átomos também saiu em quantidades quantizadas em contradição com as previsões da física clássica. O átomo de Bohr postulou uma regra de quantização de momento angular,
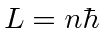 pois
pois 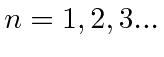 , isso deu o resultado certo para o hidrogênio, mas acabou se revelando errado, uma vez que o estado fundamental do hidrogênio tem momento angular zero. Foi necessário um conhecimento completo da Mecânica Quântica para explicar os espectros de energia atômica.
, isso deu o resultado certo para o hidrogênio, mas acabou se revelando errado, uma vez que o estado fundamental do hidrogênio tem momento angular zero. Foi necessário um conhecimento completo da Mecânica Quântica para explicar os espectros de energia atômica. - Espalhamento Compton: Quando a luz foi espalhada pelos elétrons, ela se comportou como uma partícula, mas muda o comprimento de onda no espalhamento; mais evidências para a natureza das partículas da luz e o postulado de Plank.
- Ondas e partículas: em experimentos de difração, a luz mostrou se comportar como uma onda, enquanto em experimentos como o efeito fotoelétrico, a luz se comportou como uma partícula. Experimentos de difração mais difíceis mostraram que os elétrons (assim como as outras partículas) também se comportavam como uma onda, mas só podemos detectar um número inteiro de elétrons (ou fótons).
A Mecânica Quântica incorpora uma dualidade onda-partícula e explica todos os fenômenos acima. Ao fazer isso, a Mecânica Quântica muda nossa compreensão da natureza de maneiras fundamentais. Enquanto as leis clássicas da física são determinísticas, QM é probabilística. Podemos apenas prever a probabilidade de uma partícula ser encontrada em alguma região do espaço.
Ondas eletromagnéticas como a luz são feitas de partículas que chamamos de fótons. Einstein, com base na fórmula de Plank, formulou a hipótese de que as partículas de luz tinham energia proporcional à sua frequência.
A nova ideia da Mecânica Quântica é que a probabilidade de cada partícula (em função da posição e do tempo) é igual ao quadrado de uma função de amplitude de probabilidade e que essas amplitudes de probabilidade obedecem a uma equação de onda. É muito parecido com o caso do eletromagnetismo, onde a densidade de energia é como o quadrado do campo e, portanto, a densidade de probabilidade do fóton é como o quadrado do campo, embora o campo seja feito de ondas. Portanto, as amplitudes de probabilidade são como os campos que conhecemos do eletromagnetismo em muitos aspectos.
DeBroglie assumiu ![]() para fótons e outras partículas e usou a invariância de Lorentz (da relatividade especial) para derivar o comprimento de onda de partículas como elétrons.
para fótons e outras partículas e usou a invariância de Lorentz (da relatividade especial) para derivar o comprimento de onda de partículas como elétrons.
O resto da mecânica ondulatória foi construída em torno dessas idéias, dando uma imagem completa que poderia explicar as medições acima e poderia ser testada com uma precisão muito alta, particularmente no átomo de hidrogênio. Passaremos vários capítulos explorando essas idéias.
* Exemplo: Suponha que o fóton seja uma partícula com o comprimento de onda deBroglie padrão. Use a cinemática para derivar o comprimento de onda do fóton espalhado como uma função do ângulo para a dispersão de Compton. *
Gasiorowicz Capítulo 1
Capítulos Rohlf 3,6
Griffiths realmente não cobre isso.
Cohen-Tannoudji et al. Capítulo
Radiação de corpo negro *
Um corpo negro é aquele que absorve toda a radiação EM (luz ...) que o atinge. Para ficar em equilíbrio térmico, ele deve emitir radiação na mesma taxa em que a absorve, de modo que um corpo negro também irradie bem. (Fogões são pretos.)
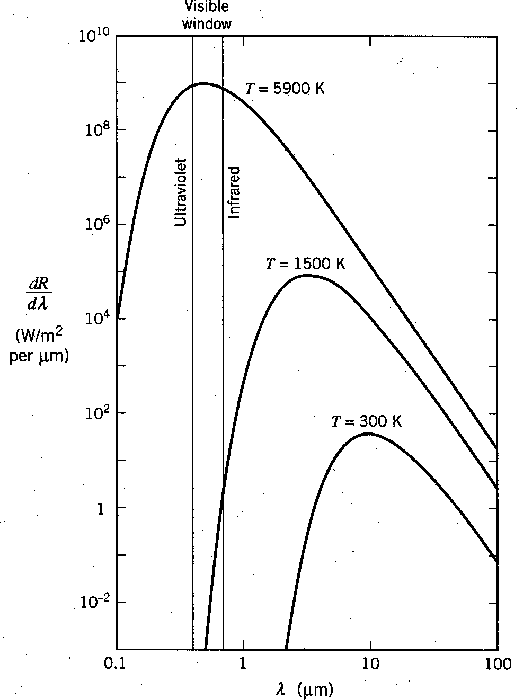
A radiação de um objeto quente é familiar para nós. Objetos em torno da temperatura ambiente irradiam principalmente no infravermelho, como pode ser visto no gráfico abaixo.
Se aquecermos um objeto até cerca de 1.500 graus, começaremos a ver um brilho vermelho opaco e diremos que o objeto está incandescente. Se aquecermos algo até cerca de 5000 graus, perto da temperatura da superfície do Sol, ela irradia bem por todo o espectro visível e dizemos que é branco quente.
Ao considerar as placas em equilíbrio térmico, pode-se mostrar que a potência emissiva sobre o coeficiente de absorção deve ser a mesma em função do comprimento de onda, mesmo para placas de materiais diferentes.
Se houvesse diferenças, poderia haver um fluxo líquido de energia de uma placa para a outra, violando a condição de equilíbrio.
Um corpo negro é aquele que absorve toda a radiação incidente sobre ele.
Assim, o poder Emissivo do corpo negro,, 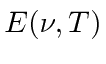 é universal e pode ser derivado dos primeiros princípios.
é universal e pode ser derivado dos primeiros princípios.
Um bom exemplo de corpo negro é uma cavidade com um pequeno orifício. Qualquer luz incidente sobre o orifício entra na cavidade e essencialmente nunca é refletida, uma vez que teria que sofrer um grande número de reflexos nas paredes da cavidade. Se tornarmos as paredes absorventes (talvez pintando-as de preto), a cavidade formará um corpo preto perfeito.
Há uma relação simples entre a densidade de energia em uma cavidade  e o poder emissivo de corpo negro de um corpo negro que simplesmente vem de uma análise de quanta radiação, viajando na velocidade da luz, fluirá de um buraco no cavidade em um segundo.
e o poder emissivo de corpo negro de um corpo negro que simplesmente vem de uma análise de quanta radiação, viajando na velocidade da luz, fluirá de um buraco no cavidade em um segundo.
A única parte que requer um pouco de reflexão é o 4 na equação acima.
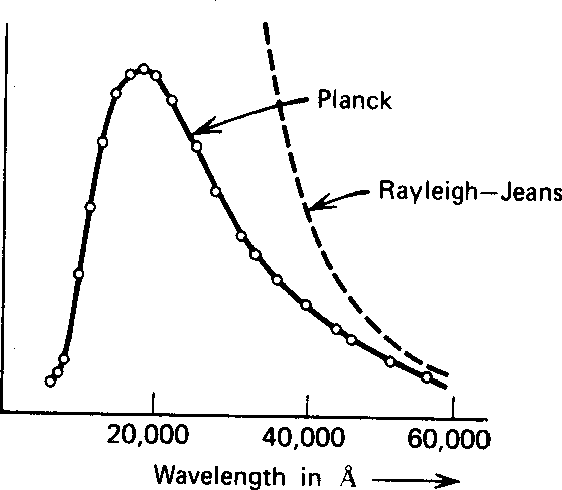
Rayleigh e Jeans calculado t ele densidade de energia (em ondas EM) no interior de uma cavidade e, por conseguinte, o espectro de emissão de um corpo negro. Seu cálculo foi baseado na teoria EM simples e equipartição. Não apenas não concordou com os dados; dizia que toda a energia seria irradiada instantaneamente em radiação EM de alta frequência. Isso foi chamado de catástrofe ultravioleta .
Plank encontrou uma fórmula que se ajusta bem aos dados em comprimentos de onda longos e curtos.
Sua fórmula se ajustou aos dados tão bem que ele tentou encontrar uma maneira de derivá-los. Em poucos meses, ele foi capaz de fazer isso, postulando que a energia era emitida em quanta com ![]() . Embora haja um grande número de modos de cavidade em alta frequência, a probabilidade de emitir tais quanta de alta energia desaparece exponencialmente de acordo com a distribuição de Boltzmann. Assim, Plank suprimiu a radiação de alta frequência no cálculo e concordou com o experimento. Observe que a fórmula de corpo negro de Plank é a mesma no limite que
. Embora haja um grande número de modos de cavidade em alta frequência, a probabilidade de emitir tais quanta de alta energia desaparece exponencialmente de acordo com a distribuição de Boltzmann. Assim, Plank suprimiu a radiação de alta frequência no cálculo e concordou com o experimento. Observe que a fórmula de corpo negro de Plank é a mesma no limite que 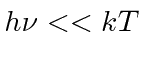 vai para zero em geral,
vai para zero em geral, ![]() enquanto a fórmula de Rayleigh vai para o infinito.
enquanto a fórmula de Rayleigh vai para o infinito.
É interessante notar que as ondas EM clássicas sugariam toda a energia térmica da matéria, tornando o universo um lugar muito frio para nós. A figura abaixo compara os dois cálculos com alguns dados em ![]() graus. (Também é surpreendente que o início da revolução quântica tenha vindo da radiação do corpo negro.)
graus. (Também é surpreendente que o início da revolução quântica tenha vindo da radiação do corpo negro.)
Portanto, a potência emissiva por unidade de área é
Podemos integrar isso sobre frequência para obter a potência total irradiada por unidade de área.
Exemplo: Qual é a temperatura na superfície solar? Use a intensidade da radiação na Terra e o pico do espectro em cerca de 500 nm para obter respostas. *
Exemplo: O fundo de micro-ondas cósmico é uma radiação de corpo negro com uma temperatura de 2,7 graus. Para qual frequência (e qual comprimento de onda) a intensidade atinge o pico? *
O efeito fotoelétrico
O efeito fotoelétrico mostra que a hipótese de Plank, usada para ajustar os dados do corpo negro, é realmente correta para a radiação EM. Einstein foi mais longe e propôs, em 1905, que a luz era composta de partículas com energia relacionada à frequência da luz ![]() . (Ele recebeu seu prêmio Nobel pelo efeito fotoelétrico, não por Relatividade Especial ou Geral.)
. (Ele recebeu seu prêmio Nobel pelo efeito fotoelétrico, não por Relatividade Especial ou Geral.)
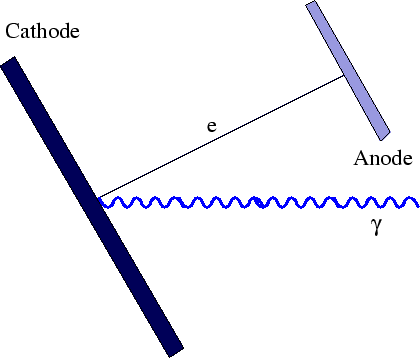
Quando a luz atinge uma superfície polida (metal), os elétrons são ejetados.
As medições foram feitas da energia máxima do elétron versus frequência e intensidade da luz. A física clássica previu que a energia do elétron deveria aumentar com a intensidade, conforme o campo elétrico aumenta. Isso não é observado. A energia do elétron é independente da intensidade e depende linearmente da freqüência da luz, como pode ser visto na figura acima. A energia cinética dos elétrons é dada pela constante de Plank vezes a frequência da luz menos uma função de trabalho ![]() que depende do material.
que depende do material.
Esta equação apenas expressa a conservação da energia ![]() sendo a energia do fóton e
sendo a energia do fóton e ![]() a energia de ligação dos elétrons no sólido. Os dados do efeito fotoelétrico apoiaram fortemente a hipótese de que a luz é composta de partículas (fótons).
a energia de ligação dos elétrons no sólido. Os dados do efeito fotoelétrico apoiaram fortemente a hipótese de que a luz é composta de partículas (fótons).
O átomo de Rutherford *
A teoria clássica dos átomos afirmava que os elétrons estavam ligados a uma grande carga positiva do tamanho do átomo. Rutherford espalhou ![]() partículas carregadas ( ) dos átomos para ver qual era a distribuição de carga positiva. Com uma distribuição de carga aproximadamente uniforme, suas
partículas carregadas ( ) dos átomos para ver qual era a distribuição de carga positiva. Com uma distribuição de carga aproximadamente uniforme, suas ![]() partículas de 5,5 MeV nunca deveriam ter retrodifundido porque tinham energia suficiente para superar a força coulomb de uma distribuição de carga, essencialmente arando direto pelo meio.
partículas de 5,5 MeV nunca deveriam ter retrodifundido porque tinham energia suficiente para superar a força coulomb de uma distribuição de carga, essencialmente arando direto pelo meio.
Ele descobriu que as ![]() partículas costumavam se espalhar em ângulos maiores que 90 graus. Seus dados podem ser explicados se o núcleo positivo de um átomo for muito pequeno. Para um núcleo muito pequeno, a força de Coulomb continua a aumentar à medida que se
partículas costumavam se espalhar em ângulos maiores que 90 graus. Seus dados podem ser explicados se o núcleo positivo de um átomo for muito pequeno. Para um núcleo muito pequeno, a força de Coulomb continua a aumentar à medida que se ![]() aproxima do núcleo, e o retroespalhamento é possível.
aproxima do núcleo, e o retroespalhamento é possível.
Exemplo: Use a eletrostática para estimar o quão pequeno um núcleo de ouro deve ser para retroespalhar uma partícula alfa de 5,5 MeV. *
Isso trouxe um novo problema. O tamanho atômico era conhecido por vários tipos de experimentos. Se os elétrons orbitam em torno do núcleo atômico , de acordo com as equações de Maxwell, eles devem irradiar energia à medida que se aceleram. Esta radiação não é observada e os estados básicos dos átomos são estáveis.
Na Mecânica Quântica, a localização do elétron ao redor do núcleo é limitada por causa da natureza ondulatória do elétron . Para o hidrogênio, onde não há problema de múltiplos corpos para tornar o cálculo desnecessariamente difícil, os níveis de energia podem ser calculados com muita precisão. O hidrogênio foi usado para testar a mecânica quântica à medida que se desenvolvia. Também usaremos bastante hidrogênio neste curso.
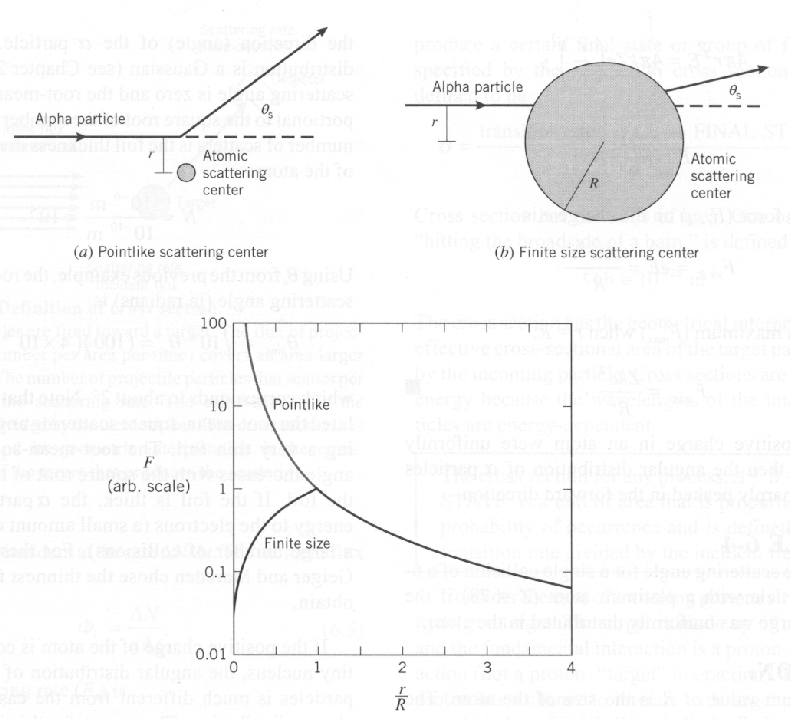
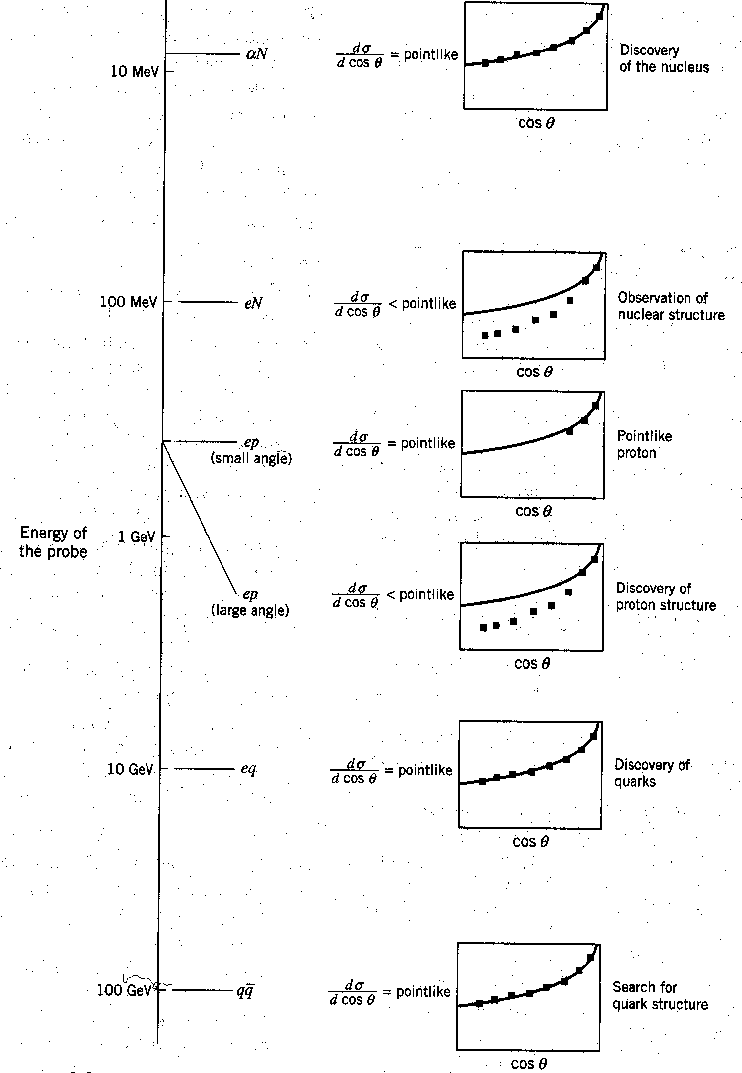
O espalhamento das ![]() partículas de alta energia permitiu a Rutherford "ver" dentro do átomo e determinar que o núcleo atômico é muito pequeno. (Ele provavelmente destruiu todos os átomos que "viu".) A figura abaixo mostra a distribuição angular de Rutherford em seu experimento de espalhamento junto com vários usos subsequentes da mesma técnica, com partículas de energia cada vez mais altas. Vemos a descoberta de Rutherford do minúsculo núcleo , a descoberta da estrutura nuclear , a descoberta de um próton pontual dentro do núcleo , a descoberta da estrutura do próton , a descoberta de quarks dentro do próton e, finalmente, a falta de descoberta, até agora , de qualquerestrutura de quark .
partículas de alta energia permitiu a Rutherford "ver" dentro do átomo e determinar que o núcleo atômico é muito pequeno. (Ele provavelmente destruiu todos os átomos que "viu".) A figura abaixo mostra a distribuição angular de Rutherford em seu experimento de espalhamento junto com vários usos subsequentes da mesma técnica, com partículas de energia cada vez mais altas. Vemos a descoberta de Rutherford do minúsculo núcleo , a descoberta da estrutura nuclear , a descoberta de um próton pontual dentro do núcleo , a descoberta da estrutura do próton , a descoberta de quarks dentro do próton e, finalmente, a falta de descoberta, até agora , de qualquerestrutura de quark .
Para "ver'' essas coisas em distâncias cada vez menores, precisamos usar feixes de partículas com comprimento de onda cada vez menor e, portanto, com energia mais alta.
Espectro Atômico *
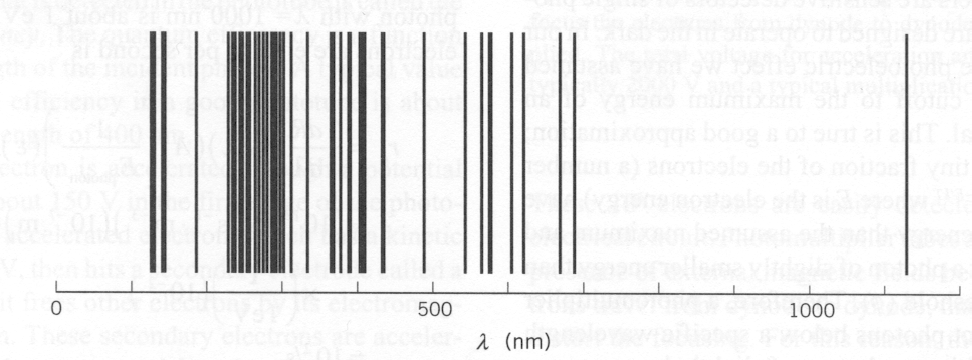
O hidrogênio foi, em última análise, o verdadeiro teste da teoria quântica. Medições de altíssima precisão foram feitas usando grades de difração. Estes foram bem compreendidos na QM não relativística e compreendidos ainda melhor na Teoria Quântica de Campos totalmente relativística, Eletrodinâmica Quântica.
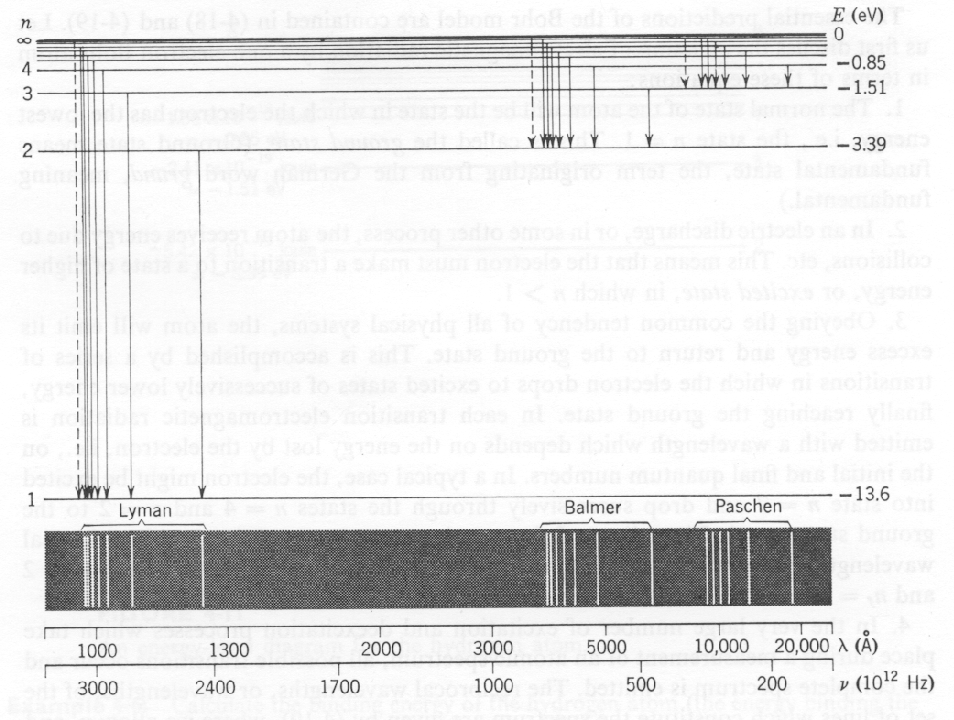
A figura abaixo mostra os níveis de energia em hidrogênio , as transições entre os níveis de energia e o comprimento de onda da luz produzida na transição. A série Lyman cobre as transições para o estado fundamental e está além da parte visível do espectro. A série Balmer é devida a transições para o primeiro estado excitado e está no visível.
Na época de Plank ![]() , muitos dados existiam sobre as energias discretas nas quais os átomos irradiavam. Cada átomo tinha sua impressão digital de radiação única. Absorção em energias discretas também foi observada.
, muitos dados existiam sobre as energias discretas nas quais os átomos irradiavam. Cada átomo tinha sua impressão digital de radiação única. Absorção em energias discretas também foi observada.
A fórmula de Rydberg para as energias dos fótons emitidos pelo hidrogênio foi desenvolvida bem antes da explicação QM aparecer.
Alguns dos estados nos átomos mais pesados seguiram o mesmo tipo de fórmula. Melhores experimentos mostraram que as linhas espectrais eram freqüentemente divididas em um multipleto de linhas. Vamos entender essas divisões muito mais tarde no curso.
Átomos mais pesados fornecem um espectro ainda mais rico, mas são muito mais difíceis de calcular. Muito boas técnicas de aproximação foram desenvolvidas. Com computadores e boa técnica, os níveis de energia de átomos mais complexos podem ser calculados. O espectro de mercúrio mostrado abaixo tem muito mais linhas do que as vistas em hidrogênio.
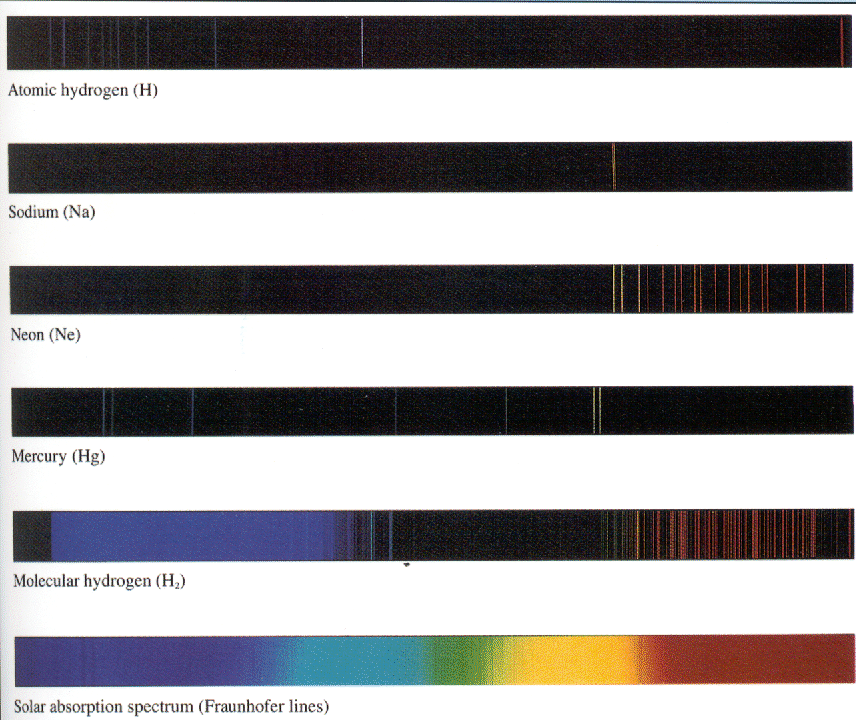
A figura abaixo mostra a parte visível do espectro para várias fontes atômicas ou moleculares. Para o Hidrogênio, vemos principalmente a série Balmer, com uma linha da Paschen-Bach. Os espectros de diferentes átomos são bastante distintos. As moléculas têm muitos outros tipos de excitações e podem produzir muitas frequências de luz.
O átomo de Bohr
Bohr postulou que os elétrons orbitavam o núcleo como planetas orbitando o sol. Ele conseguiu ajustar os dados para o Hidrogênio postulando que os elétrons orbitavam o núcleo em órbitas circulares, e que o momento angular é quantizado de forma que ![]() , para
, para 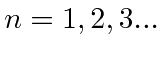 . Isso é natural, pois
. Isso é natural, pois ![]() tem unidades de momento angular. Bohr postou corretamente as energias do hidrogênio e o tamanho do átomo.
tem unidades de momento angular. Bohr postou corretamente as energias do hidrogênio e o tamanho do átomo.
Equilíbrio de forças para órbitas circulares.
Suposição de quantização de momento angular.
Resolva a velocidade.
Conecte a equação de força para obter a fórmula ![]() .
.
Agora queremos apenas conectar ![]() e
e ![]() entrar na fórmula de energia. Escrevemos o potencial de hidrogênio em termos da constante de estrutura fina .
entrar na fórmula de energia. Escrevemos o potencial de hidrogênio em termos da constante de estrutura fina . 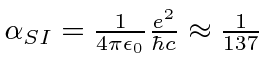
Agora calculamos os níveis de energia.
O eV constante . A fórmula de Bohr fornece o espectro de energia do hidrogênio correto .
Também podemos calcular o raio do estado fundamental da órbita de Bohr.
Isso também é sobre o raio certo. O nome desse número, raio de Bohr , persiste até hoje, apesar do fato de que a suposição de Bohr está errada.
Embora o momento angular seja quantizado em unidades de ![]() , o estado fundamental do Hidrogênio tem momento angular zero . Isso colocaria o elétron de Bohr no núcleo.
, o estado fundamental do Hidrogênio tem momento angular zero . Isso colocaria o elétron de Bohr no núcleo.
Bohr ajustou os dados, com algum elemento de verdade, mas seu modelo está ERRADO .
Derivações e Cálculos
Black Body Radiation Formulas *
Ainda não disponível
A constante de estrutura fina e o potencial de Coulomb
Vamos agora enfrentar pela primeira vez o problema de qual conjunto de unidades usar. Textos avançados normalmente usam unidades CGS em que a energia potencial é
enquanto as unidades internacionais padrão
Podemos contornar o problema definindo a constante de estrutura fina adimensional ![]() .
.
Portanto, em qualquer conjunto de unidades, o potencial de hidrogênio é
Exemplos
A Temperatura Solar
Estime a temperatura solar usando
- a intensidade da radiação solar na terra de 1,4 quilowatts por metro quadrado. ( m, m)
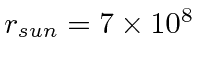
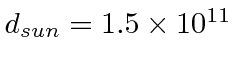
- e o espectro solar que atinge o pico a cerca de 500 nm.
Primeiro, calculamos a energia irradiada por unidade de área na superfície solar.
Comparamos isso com a expectativa em função da temperatura.
e pegue
Vamos supor que os 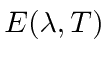 picos sejam de 500 nm, como mostra um dos gráficos. Precisamos nos transformar
picos sejam de 500 nm, como mostra um dos gráficos. Precisamos nos transformar 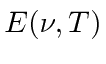 . Lembre-se de funções de distribuição.
. Lembre-se de funções de distribuição. 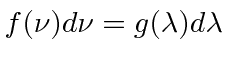
Este pico quando
é máximo.
Vamos definir 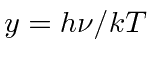 e resolver a equação
e resolver a equação
Resolvi isso iterativamente começando em y = 5 e comecei a 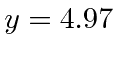 sugerir
sugerir
Isso concorda bem.
Radiação de corpo negro do universo inicial *
Encontre a frequência ![]() em que o Emissivo
em que o Emissivo 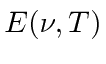 é máximo para a radiação cósmica de fundo de 2,7 graus. Encontre o comprimento
é máximo para a radiação cósmica de fundo de 2,7 graus. Encontre o comprimento ![]() de onda
de onda 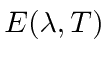 máximo.
máximo.
A radiação cósmica de fundo foi produzida quando o universo era muito mais quente do que agora. A maioria dos átomos do universo era ionizada e os fótons interagiam frequentemente com os íons ou elétrons livres. À medida que o universo esfriava, formando átomos neutros, os fótons se separavam da matéria e se propagavam pelo espaço. Hoje vemos esses fótons como a radiação de fundo. Como o universo está se expandindo, a radiação mudou para uma temperatura muito mais baixa do vermelho. Observamos cerca de 2,7 graus. A radiação de fundo é muito uniforme, mas estamos começando a observar não uniformidades no ![]() nível.
nível.
Do problema anterior, podemos dizer que o pico ![]() ocorre quando
ocorre quando
Da mesma forma, o pico ![]() ocorre quando
ocorre quando
Dispersão Compton *
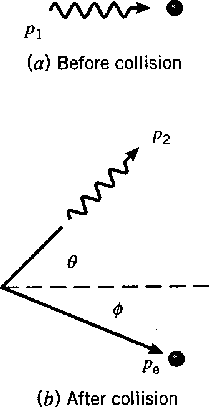
Compton espalhou fótons de alta energia (essencialmente) de elétrons livres em 1923. Ele mediu o comprimento de onda dos fótons espalhados como uma função do ângulo de espalhamento. A figura abaixo mostra o estado inicial (a) e o estado final, com o fóton espalhado por um ângulo ![]() e o elétron recuando em um ângulo
e o elétron recuando em um ângulo ![]() . Os fótons eram provenientes do decaimento nuclear e, portanto, eram de energia alta o suficiente para que não importasse que os elétrons estivessem realmente ligados aos átomos. Queremos derivar a fórmula para o comprimento de onda do fóton espalhado em função do ângulo .
. Os fótons eram provenientes do decaimento nuclear e, portanto, eram de energia alta o suficiente para que não importasse que os elétrons estivessem realmente ligados aos átomos. Queremos derivar a fórmula para o comprimento de onda do fóton espalhado em função do ângulo .
Resolvemos o problema usando apenas a conservação de energia e momento. Vamos trabalhar em unidades em que ![]() por enquanto. Colocaremos as
por enquanto. Colocaremos as ![]() costas no final. Suponha que o fóton esteja inicialmente se movendo na
costas no final. Suponha que o fóton esteja inicialmente se movendo na ![]() direção com energia E e que ele se espalhe no
direção com energia E e que ele se espalhe no ![]() plano de forma que
plano de forma que 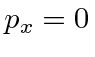 . A conservação do momento dá
. A conservação do momento dá
e
Conservação de energia dá
Nosso objetivo é resolver para ![]() em termos de,
em termos de, ![]() então vamos nos certificar de que eliminamos o
então vamos nos certificar de que eliminamos o ![]() . Continuando da equação de energia
. Continuando da equação de energia
quadratura e cálculo ![]() dos componentes
dos componentes
e escrever os quadrados do lado direito
e removendo coisas que aparecem em ambos os lados
e agrupamento
Já que em nossas unidades finas, 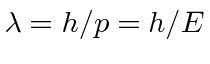
Agora aplicamos a velocidade da luz para fazer com que as unidades tenham um comprimento.
Esses cálculos podem ser bastante frustrantes se você não decidir quais variáveis deseja manter e quais deve eliminar de suas equações. Neste caso, eliminamos ![]() usando a equação de energia e computação
usando a equação de energia e computação ![]() .
.
Tamanho nuclear de Rutherford
Se a carga positiva nos átomos de ouro fosse uniformemente distribuída em uma esfera ou raio de 5 Angstroms, qual é a ![]() energia cinética máxima da partícula pela qual o
energia cinética máxima da partícula pela qual o ![]() pode ser espalhado de volta na direção de onde veio?
pode ser espalhado de volta na direção de onde veio?
Para resolver isso, precisamos calcular o potencial no centro da distribuição de carga em relação ao potencial no infinito (que diremos que é zero). Isso nos diz diretamente a energia cinética em eV necessária para arar através da distribuição de carga.
O potencial na superfície do núcleo é onde Z é o número de prótons no átomo e R é o raio nuclear. Essa é a parte fácil. Agora precisamos integrar nosso caminho para o centro. 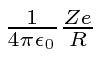
O dá a fração da carga nuclear dentro de um raio . ![]()
![]()
Então
Então, é a energia cinética em eV necessária para que uma partícula de carga ![]() atravesse o centro de uma distribuição esférica de carga. A
atravesse o centro de uma distribuição esférica de carga. A ![]() partícula realmente tem carga,
partícula realmente tem carga, 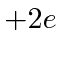 então precisamos multiplicar por 2. Para um raio nuclear de 5 Å ou metros, precisamos de cerca de 680 eV para arar através do núcleo. Para o raio nuclear real de cerca de 5 Fermis ou metros, precisamos de 68 MeV para arar.
então precisamos multiplicar por 2. Para um raio nuclear de 5 Å ou metros, precisamos de cerca de 680 eV para arar através do núcleo. Para o raio nuclear real de cerca de 5 Fermis ou metros, precisamos de 68 MeV para arar. 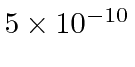
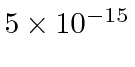
Vamos comparar os números das unidades SI acima com meu método sugerido de usar a constante de estrutura fina ... Colocando a carga alfa de ![]() .
.
Isso é mais fácil.
Problemas de teste de amostra
- Qual é o comprimento de onda máximo da radiação eletromagnética que pode ejetar elétrons de um metal com função de trabalho de 3 eV? (3 pontos)
Resposta
A energia mínima do fóton necessária para eliminar um elétron é 3 eV. Só precisamos converter isso para comprimento de onda. - Com base no eletromagnetismo clássico e na mecânica estatística, Rayleigh calculou a densidade de energia dentro de uma cavidade. Ele descobriu que, a uma temperatura T, a densidade de energia em função da frequência era
Por que isso está relacionado à radiação do corpo negro? Por que isso estava em desacordo óbvio com a observação? - Qual é o comprimento de onda máximo da radiação eletromagnética que pode ejetar elétrons de um metal com função de trabalho de 2 eV?
- Diga simplesmente que problema com a radiação de corpo negro fez com que Plank propusesse a relação
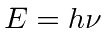 para a luz.
para a luz. - A função de trabalho de um metal é 2 eV. Suponha que um feixe de luz de comprimento de onda
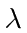 incida sobre uma superfície polida do metal. Trace a energia máxima do elétron (em eV) dos elétrons ejetados do metal
incida sobre uma superfície polida do metal. Trace a energia máxima do elétron (em eV) dos elétrons ejetados do metal 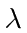 em relação aos Angstroms. Certifique-se de rotular ambos os eixos com alguns valores numéricos.
em relação aos Angstroms. Certifique-se de rotular ambos os eixos com alguns valores numéricos.