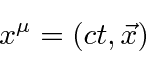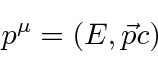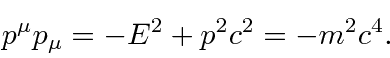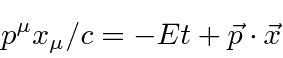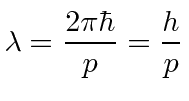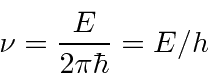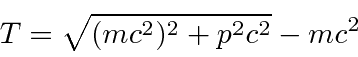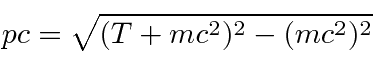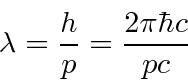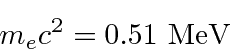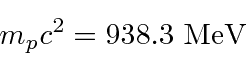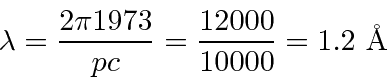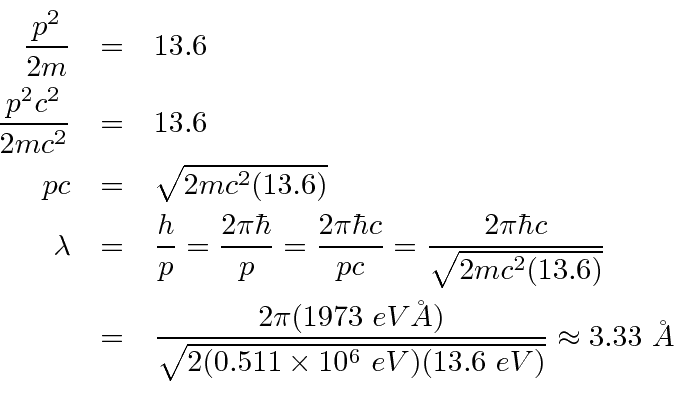Feynman Lectures, Volume III, Capítulo I.
Gasciorawicz realmente não faz isso.
Capítulos 5 de Rohlf
Griffiths não cobre isso.
Difração de Duas Fendas
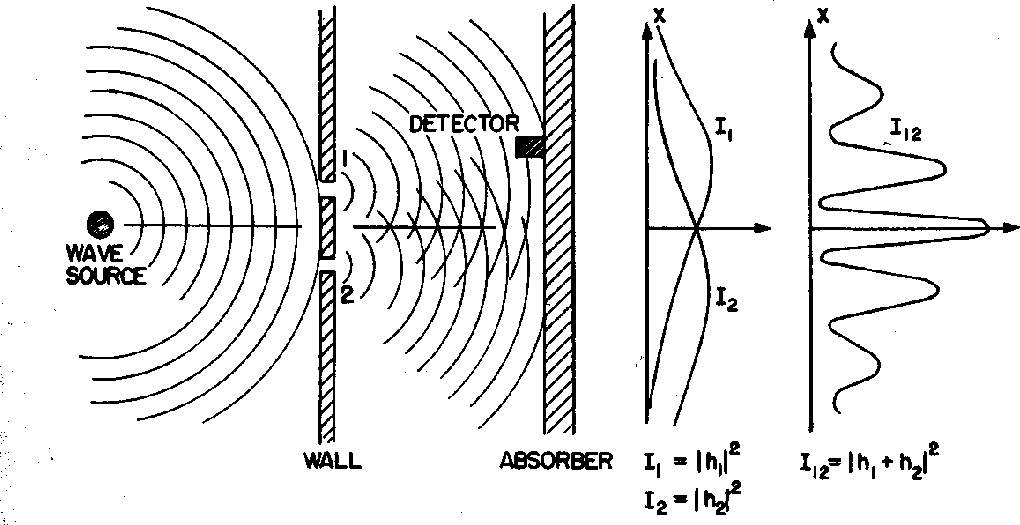
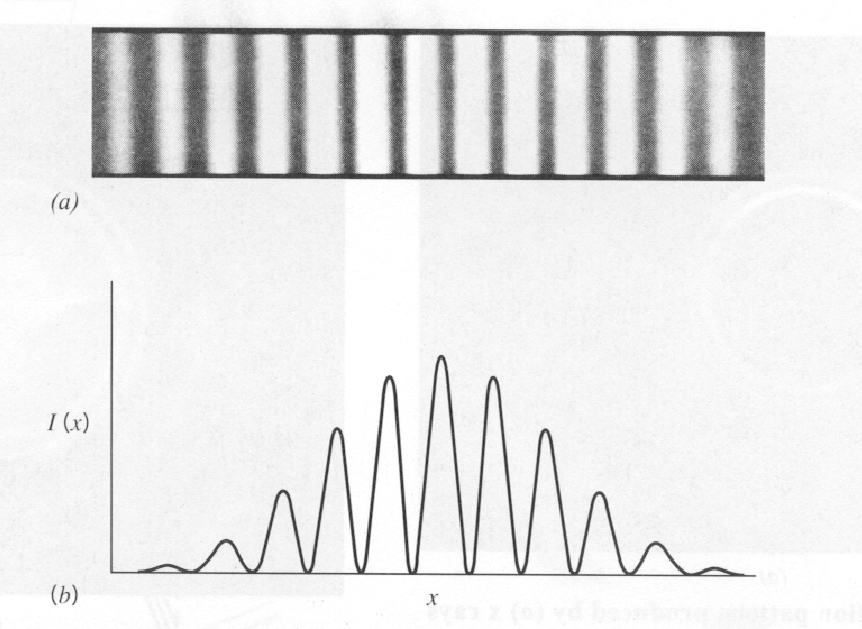
As ondas de água exibirão um padrão de interferência difrativa em um experimento de 2 fendas, conforme diagramado abaixo. O diagrama mostra as cristas das ondas de água em algum momento. A jusante das fendas, veremos a interferência construtiva onde as ondas das fendas estão em fase e a interferência destrutiva onde estão 180 graus defasados, por exemplo, onde uma crista de uma fenda encontra uma depressão da outra. O gráfico marcado ![]() mostra o padrão de interferência no local do absorvedor. A difração é um fenômeno de onda simples .
mostra o padrão de interferência no local do absorvedor. A difração é um fenômeno de onda simples .
A difração da luz era um fenômeno bem conhecido no final do século 19 e era bem explicado na teoria eletromagnética clássica, uma vez que a luz era considerada uma onda EM. O padrão de difração de duas fendas estreitas é particularmente fácil de entender em termos de ondas. A configuração é mostrada no diagrama abaixo.
As ondas EM de comprimento de onda ![]() são emitidas por uma única fonte de luz, como um laser. Eles viajam para duas fendas estreitas, (para simplificar) equidistantes da fonte e a uma distância uma da
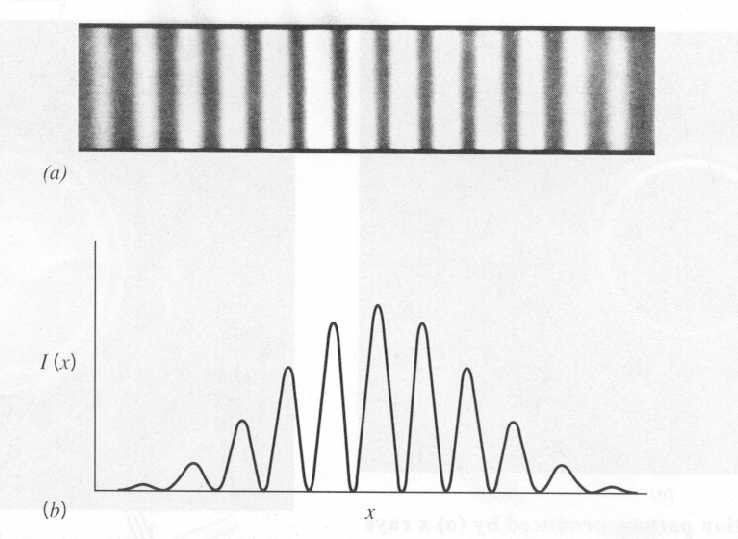
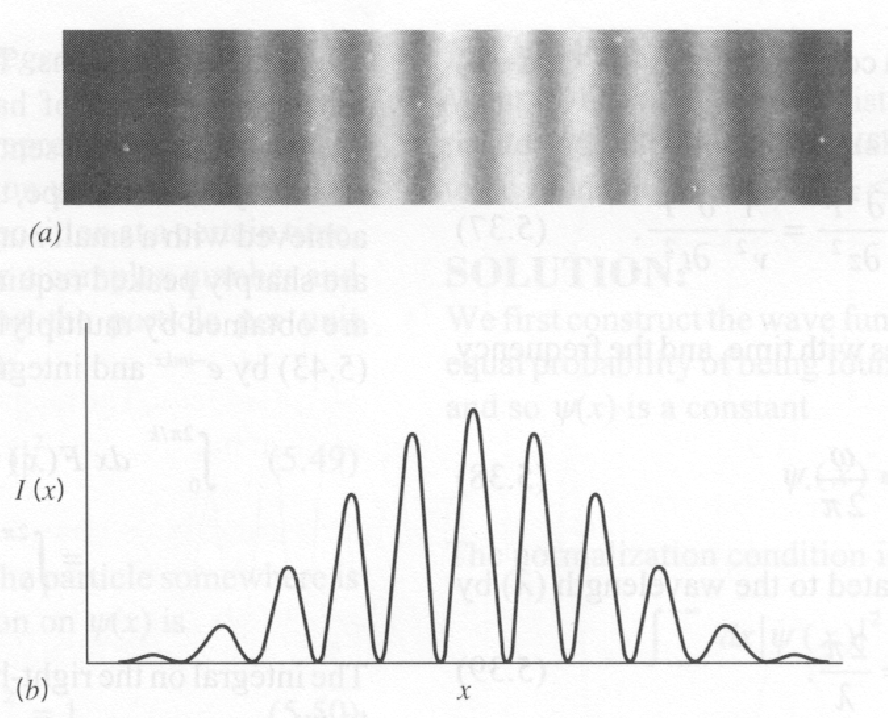
são emitidas por uma única fonte de luz, como um laser. Eles viajam para duas fendas estreitas, (para simplificar) equidistantes da fonte e a uma distância uma da ![]() outra. A luz viaja das fendas para uma tela de detecção. Um padrão de difração pode ser visto na tela de detecção, como o mostrado na imagem abaixo.
outra. A luz viaja das fendas para uma tela de detecção. Um padrão de difração pode ser visto na tela de detecção, como o mostrado na imagem abaixo.
O centro do padrão de difração ocorre no local da tela equidistante de cada fenda onde as ondas das duas fendas estão em fase (porque elas viajaram exatamente a mesma distância) e os campos se somam, então as ondas interferem construtivamente e há um máximo de intensidade. A alguma distância deste centro do padrão de difração, haverá interferência destrutiva entre as ondas das duas fendas e a intensidade será zero. Isso ocorrerá quando a distância percorrida por duas ondas for diferente em 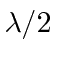 , então as ondas estão 180 graus fora de fase e os campos das duas fendas se cancelam .
, então as ondas estão 180 graus fora de fase e os campos das duas fendas se cancelam .
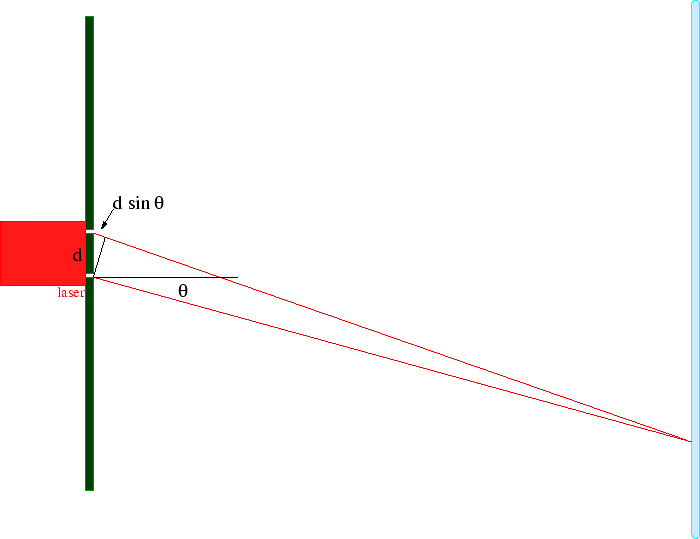
Podemos calcular esta localização observando o diagrama acima. Assumimos que a distância até a tela é muito maior do que ![]() . Para luz detectada em um ângulo
. Para luz detectada em um ângulo ![]() , a distância extra percorrida desde a fenda 1 é justa
, a distância extra percorrida desde a fenda 1 é justa ![]() . Portanto, o ângulo do primeiro mínimo (ou nulo) pode ser encontrado na equação .
. Portanto, o ângulo do primeiro mínimo (ou nulo) pode ser encontrado na equação . 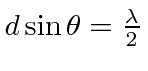
De maneira mais geral, obteremos um máximo se os caminhos das fendas diferirem em um número inteiro de comprimentos de onda e obteremos um valor nulo quando os caminhos diferirem em meio número inteiro de comprimentos de onda . . ![]()
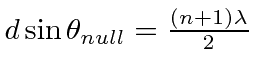
Embora seja muito difícil porque os elétrons estão carregados, a difração de elétrons de 2 fendas também foi observada.
Assim, todos os tipos de partículas parecem difratar, indicando que há algum tipo de onda envolvida. Vamos agora continuar com alguns experimentos mentais sobre difração para ilustrar a física que a Mecânica Quântica precisava corresponder.Difração de fenda única
Existem muitos outros exemplos de difração. A imagem abaixo mostra a difração de uma única fenda onde ondas de diferentes partes da fenda interferem umas nas outras. Para obter o campo em algum ponto da tela de detecção, deve-se integrar sobre a fenda.
* Exemplo: derivar a localização dos nós no padrão de difração de uma fenda de largura ![]() . Agora tente calcular a distribuição de intensidade para difração de fenda única. *
. Agora tente calcular a distribuição de intensidade para difração de fenda única. *
* Exemplo: derivar a localização dos nós no padrão de difração de duas fendas estreitas a uma distância uma da ![]() outra. Agora tente calcular a distribuição de intensidade. *
outra. Agora tente calcular a distribuição de intensidade. *
Difração de fenda única
Existem muitos outros exemplos de difração. A imagem abaixo mostra a difração de uma única fenda onde ondas de diferentes partes da fenda interferem umas nas outras. Para obter o campo em algum ponto da tela de detecção, deve-se integrar sobre a fenda.
* Exemplo: derivar a localização dos nós no padrão de difração de uma fenda de largura ![]() . Agora tente calcular a distribuição de intensidade para difração de fenda única.
. Agora tente calcular a distribuição de intensidade para difração de fenda única.
Difração de Cristais
As ondas de elétrons foram demonstradas pela primeira vez medindo a difração de cristais . Davison e Germer observaram a difração de elétrons de um cristal de níquel em 1928. Eles variaram a energia do elétron para medir o comprimento de onda do elétron, concordando bem com a expectativa de deBroglie.
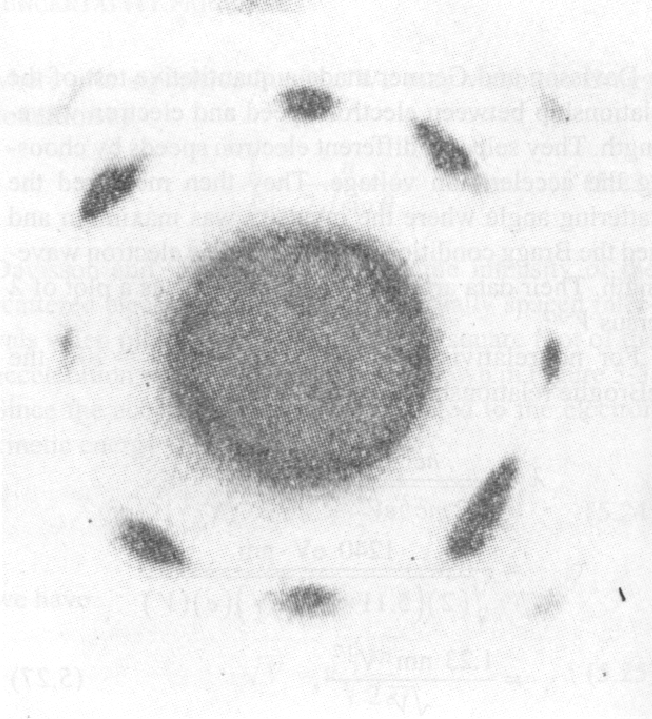
Primeiro, vemos a difração de um único cristal .
A difração de material policristalino dá anéis concêntricos em vez de pontos.
A difração de cristais é uma ferramenta poderosa. Primeiro, vemos a difração de raios-X de um único cristal de sódio que tem localizações periódicas dos átomos.
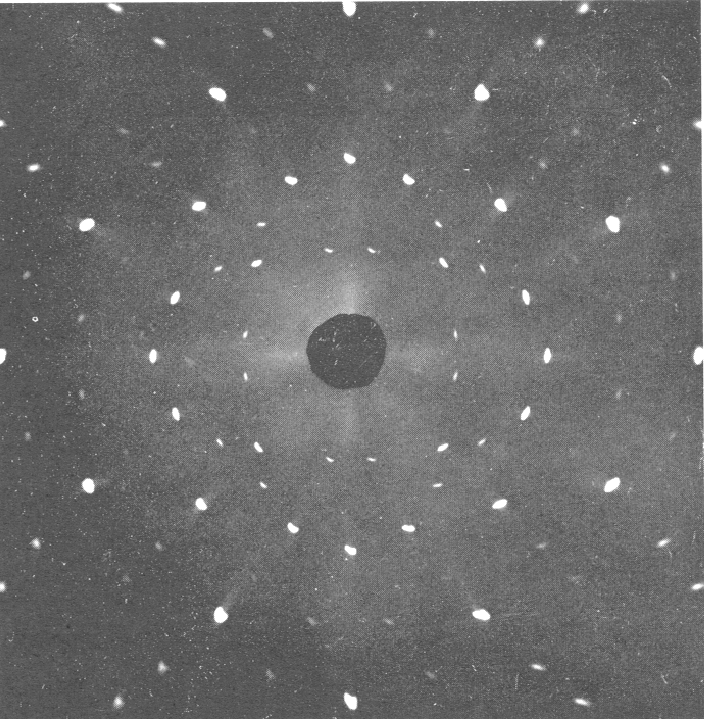
Outro exemplo de difração é mostrado abaixo. Aqui os nêutrons difratam de um único cristal de sódio .
O comprimento de onda DeBroglie
A transformação de Lorentz foi postulada para ondas eletromagnéticas antes de Einstein desenvolver a relatividade especial. As ondas EM eram inteiramente consistentes com a Relatividade. Por exemplo, a fase de uma onda EM em algum ponto é a mesma do ponto transformado de Lorentz.DeBroglie aplicou este requisito de invariância de Lorentz na fase das ondas de matéria para determinar qual deve ser o comprimento de onda. É fácil para nós derivar o comprimento de onda usando 4 vetores. Posição e tempo formam um vetor 4.
Energia e impulso formam outro.
Lembre-se de que os vetores de Lorentz devem ser transformados, mas os escalares de Lorentz são automaticamente invariantes sob transformações. Por exemplo, o escalar formado pontuando o momento 4 em si mesmo é
A massa de uma partícula é claramente invariante de Lorentz.
Para calcular o comprimento de onda de nossas ondas de matéria, vamos usar o escalar
Já é fácil ver que a fase de uma onda como
é invariante de Lorentz.
Para ler o comprimento de onda, vamos escolher a parte da expressão que corresponde a . Vemos isso e, portanto, o comprimento de onda DeBroglie é. ![]()
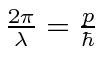
Também podemos ler a frequência ![]() .
.
Em certo sentido, essa foi a entrada para o nosso cálculo.
O comprimento de onda deBroglie será nosso principal input de física para o desenvolvimento da Mecânica Quântica. Não é que este trabalho tenha sido o mais significativo, mas este comprimento de onda resume a maior parte do que aconteceu antes de 1923.
Computando comprimentos de onda DeBroglie
Costumamos citar a energia de uma partícula em termos de sua energia cinética em Volts, eV do elétron (ou Volts do Milhão de elétrons, MeV). A razão para isso é que as partículas são geralmente aceleradas para alguma energia por um campo elétrico. Se eu deixar um elétron (ou próton ...) ser acelerado por uma diferença de potencial de 100 Volts, ele terá uma energia cinética de 100eV.
Todo o problema de calcular um comprimento de onda deBroglie é converter a energia cinética em momento. Se você sempre quer estar correto sem nenhuma necessidade de pensar, use a fórmula relativisticamente correta para a energia cinética
em seguida, use esta fórmula útil para obter a resposta.
Lembro-me disso permitindo-me manter todo o cálculo em eV. Eu também conheço as massas das partículas. ![]()
(Se 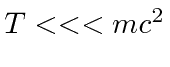 , certifique-se de que a precisão de sua calculadora é suficiente ou use o método não relativístico abaixo.)
, certifique-se de que a precisão de sua calculadora é suficiente ou use o método não relativístico abaixo.)
Se você sabe que a partícula é super-relativista , de modo que 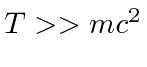 , em seguida, basta usar
, em seguida, basta usar 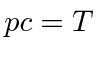 ea vida é fácil.
ea vida é fácil.
Se você sabe que a partícula é altamente não-relativista , 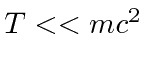 , então você pode usar doação .
, então você pode usar doação . 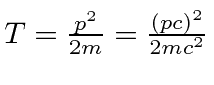
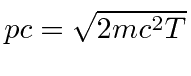
Então, por exemplo, calcule o comprimento de onda de um elétron de 100 eV. Isso é não relativístico, pois 100 eV «510000 eV. Então eV ou 10000 eV. 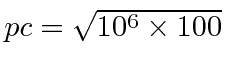
Dualidade de partícula de onda (experimentos de pensamento)
Richard Feynman (Prêmio Nobel de Eletrodinâmica Quântica ...) apresenta vários experimentos mentais em suas Lectures on Physics, terceiro volume.
Para nosso primeiro experimento mental, consideraremos duas difração de luz de silte . Suponha que, em vez de usar a tela, eu use um fotodetector sensível . Medo a intensidade da luz em função da posição perto da tela e encontro o mesmo conjunto de máximos e mínimos que fiz usando meus olhos.
Agora vamos diminuir a intensidade da fonte de luz. Para intensidade muito baixa, acho que meu detector coleta um fóton por vez . Nunca coleta meio fóton. (Com o detector certo, eu poderia verificar novamente que, para cada fóton, o efeito fotoelétrico é visto e tal ![]() .) Então as ondas que estão difratando são de alguma forma formadas por fótons. Com uma intensidade suficientemente baixa , posso garantir que apenas um fóton está presente no aparelho por vez. Posso operar meu detector e coletar dados por um longo tempo, somando o número de fótons detectados em função da posição. O que vou receber pela distribuição? Eu obtenho exatamente a mesma distribuição de antes com máximos e mínimos. Não importa quão baixa seja a intensidade, (1 partícula / minuto!)ainda vemos difração . Nunca detectamos uma fração de um elétron ou um fóton, apenas números inteiros .
.) Então as ondas que estão difratando são de alguma forma formadas por fótons. Com uma intensidade suficientemente baixa , posso garantir que apenas um fóton está presente no aparelho por vez. Posso operar meu detector e coletar dados por um longo tempo, somando o número de fótons detectados em função da posição. O que vou receber pela distribuição? Eu obtenho exatamente a mesma distribuição de antes com máximos e mínimos. Não importa quão baixa seja a intensidade, (1 partícula / minuto!)ainda vemos difração . Nunca detectamos uma fração de um elétron ou um fóton, apenas números inteiros .
Como um único fóton interfere em si mesmo? Deve de alguma forma passar por ambas as fendas.
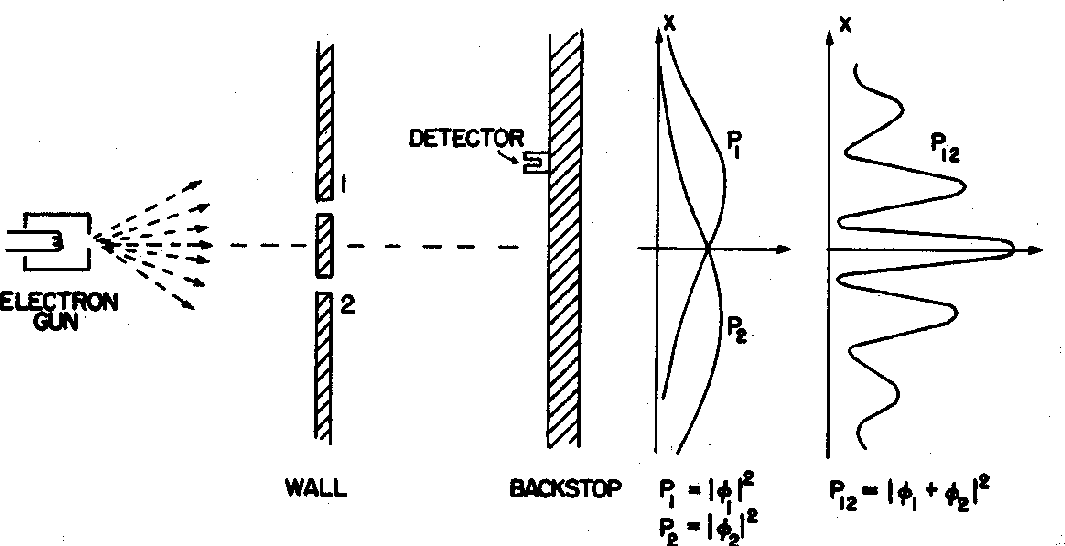
Vamos voltar para a difração de elétrons por um minuto. Em nosso experimento mental, novamente temos duas fendas.
Usamos nosso detector para medir o padrão de difração semelhante ao dos fótons rotulados 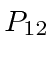 abaixo. Se cobrirmos a fenda 2 , obteremos a distribuição rotulada
abaixo. Se cobrirmos a fenda 2 , obteremos a distribuição rotulada ![]() e se / emphtextcovermos a fenda 1 obtermos a distribuição de intensidade rotulada
e se / emphtextcovermos a fenda 1 obtermos a distribuição de intensidade rotulada ![]() . Poderíamos ter feito o mesmo com nossos fótons acima.
. Poderíamos ter feito o mesmo com nossos fótons acima.
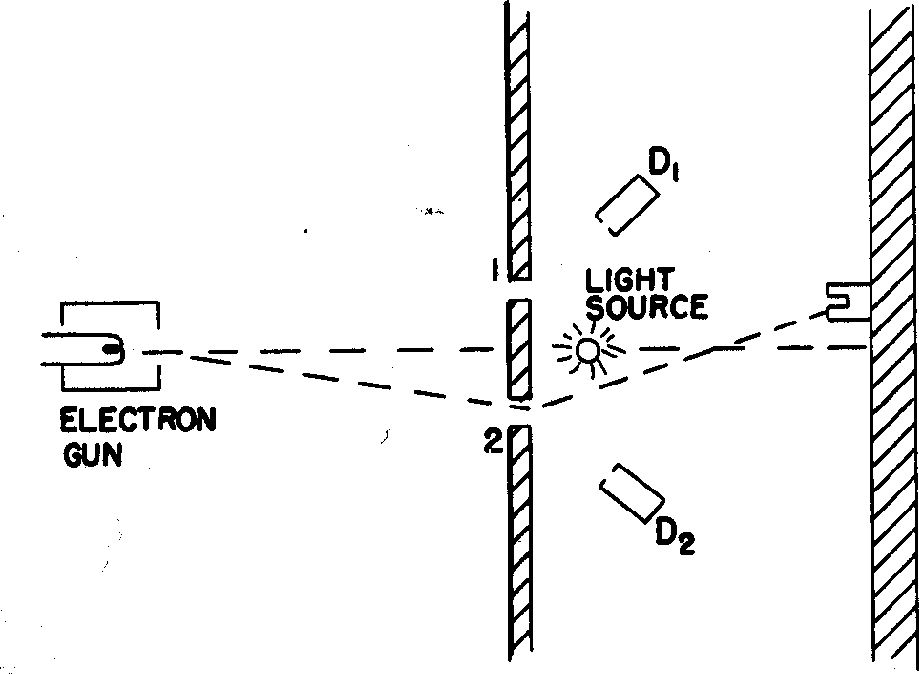
Agora tentaremos ver por qual fenda cada elétron passa. Colocamos uma fonte de luz brilhante perto das fendas e detectamos a luz refletida no elétron para que possamos ver por qual fenda ele passa.
Que distribuição vemos agora? Na verdade, veremos 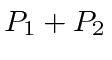 se podemos dizer por qual fenda o elétron passou. Nossa observação do elétron ao passar pela fenda mudou a distribuição de intensidade resultante . Se desligarmos a luz, voltamos a medir
se podemos dizer por qual fenda o elétron passou. Nossa observação do elétron ao passar pela fenda mudou a distribuição de intensidade resultante . Se desligarmos a luz, voltamos a medir 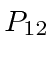 .
.
Você pode explicar por que a luz faz com que o padrão de difração desapareça?
É a mera observação? A luz muda a fase do elétron?
Existem muitos exemplos de um observador alterando o resultado de um experimento Quantum. Na verdade, é sustentado que quando um estado é observado, sua função de onda colapsa no estado `` visto ''. Nesse caso, bastava acender a luz. Não precisamos olhar.
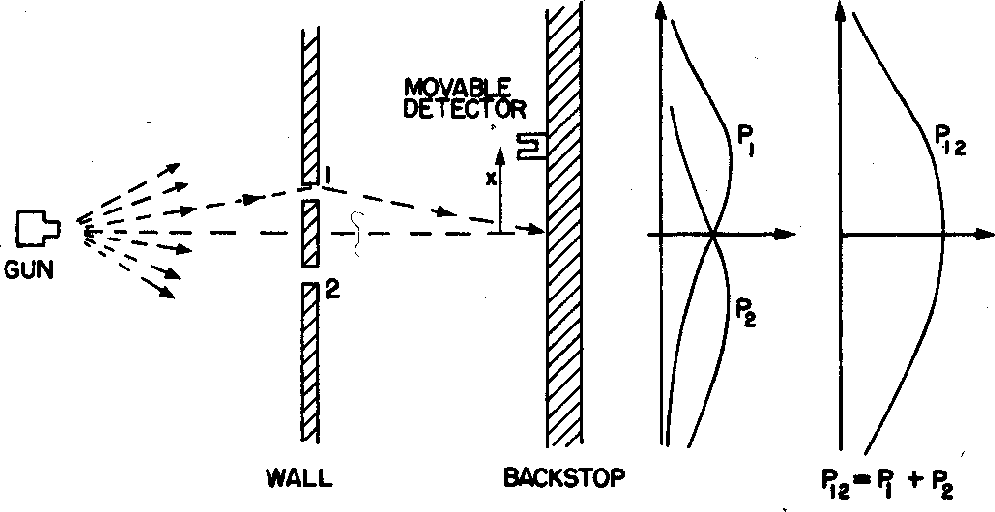
Finalmente, faremos um experimento de difração de duas fendas com balas . Devemos fazer fendas grandes o suficiente para as balas passarem.
Não importa a distância entre as fendas que escolhemos, nunca observamos difração para as balas. Eles sempre fornecem o 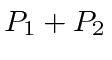 padrão (provavelmente diferente para os marcadores). Você pode explicar isso?
padrão (provavelmente diferente para os marcadores). Você pode explicar isso?
O comprimento de onda da bala é muito menor do que o tamanho real da bala.
Por que não vimos difração para as balas. As balas são objetos macroscópicos com grandes momentos em comparação com partículas individuais. O momento elevado implica um pequeno comprimento de onda deBroglie. Portanto, para ver a difração, devemos tornar a distância entre as fendas muito menor do que fizemos para os fótons (talvez ![]() vezes menor). Mas as balas também são grandes. Eles só passam por grandes fendas, que devem estar mais afastadas do que as fendas usadas para os fótons. Para balas, o comprimento de onda é minúsculo em comparação com qualquer fenda pela qual uma bala passaria . Portanto, nenhuma difração de bala é possível.
vezes menor). Mas as balas também são grandes. Eles só passam por grandes fendas, que devem estar mais afastadas do que as fendas usadas para os fótons. Para balas, o comprimento de onda é minúsculo em comparação com qualquer fenda pela qual uma bala passaria . Portanto, nenhuma difração de bala é possível.
Feynman Lectures on Physics, Vol. III Capítulo 1
Exemplos
Distribuição de intensidade para difração de duas fendas *
Derive a localização dos nós no padrão de difração a partir de duas fendas estreitas ![]() separadas por uma distância . Agora tente calcular a distribuição de intensidade.
separadas por uma distância . Agora tente calcular a distribuição de intensidade.
Este é um exercício de laboratório .
Distribuição de intensidade para difração de fenda única *
Derive a localização dos nós no padrão de difração de uma fenda de largura ![]() . Agora tente calcular a distribuição de intensidade para difração de fenda única.
. Agora tente calcular a distribuição de intensidade para difração de fenda única.
Este é um exercício de laboratório .
Problemas de teste de amostra
- Qual é o comprimento de onda deBroglie de um elétron com 13,6 eV de energia cinética? Qual é o comprimento de onda deBroglie de um elétron com 10 MeV de energia cinética?
A resposta
13.6 eV é muito menor, então isso não é relativístico.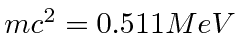
10 MeV é muito maior do que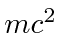 um elétron, então é super-relativístico e podemos usar
um elétron, então é super-relativístico e podemos usar 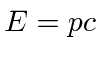 .
.
- Qual é o comprimento de onda DeBroglie para cada uma das seguintes partículas? As energias fornecidas são as energias cinéticas.
- a)
- um elétron de 10 eV
- b)
- um elétron de 1 MeV
- c)
- um próton de 10 MeV
- Um experimento de difração de elétrons de 2 fendas é configurado como (não) mostrado abaixo. A distribuição de intensidade de elétrons observada é plotada na figura. Agora, uma fonte de luz intensa é introduzida perto das duas fendas. Com esta luz, pode-se "ver" por qual fenda cada elétron passa. Faça um gráfico qualitativo da nova distribuição de intensidade do elétron de cada fenda e das 2 fendas combinadas. Qual é a condição do comprimento de onda da luz para que esse efeito ocorra?
- Qual é o comprimento de onda DeBroglie para cada uma das seguintes partículas? As energias fornecidas são as energias cinéticas.
- Qual KE deve ter um átomo de hidrogênio para que seu comprimento de onda DeBroglie seja menor que o tamanho do átomo? (Fatores de 2 não são importantes.)
- Calcule o comprimento de onda DeBroglie para (a) um próton com energia cinética de 10 MeV, (b) Um elétron com energia cinética de 10 MeV e (c) uma bola de chumbo de 1 grama movendo-se com uma velocidade de 10 cm / s (um erg é um grama cm
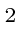 / seg
/ seg  ). Certifique-se de levar em conta a relatividade quando necessário.
). Certifique-se de levar em conta a relatividade quando necessário.