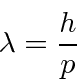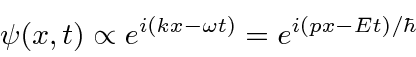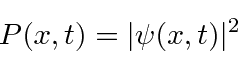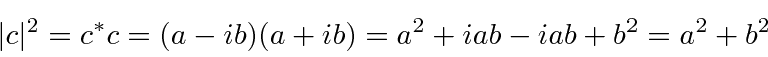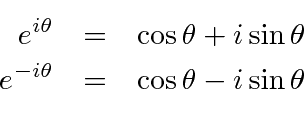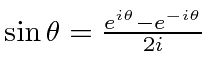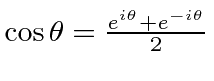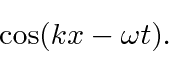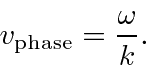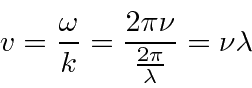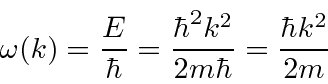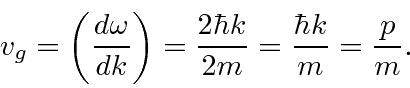A solução: Amplitudes de Probabilidade

 

Para ondas EM , a intensidade e, portanto, a probabilidade de encontrar um fóton, é proporcional ao quadrado dos campos. Os campos obedecem à equação de onda. Os campos de duas fendas podem adicionar padrões de interferência de forma construtiva ou destrutiva. Os campos \ bgroup \ color {black} $ E $ \ egroupe \ bgroup \ color {black} $ B $ \ egroupestão 90 graus defasados ​​e ambos contribuem para a intensidade.

Usaremos as mesmas idéias para elétrons , embora os detalhes do campo variem um pouco porque elétrons e fótons são tipos de partículas um tanto diferentes. Para ambas as partículas, o comprimento de onda é dado por 

\ begin {displaymath} \ bgroup \ color {black} \ lambda = {h \ over p} \ egroup \ end {displaymath}

e a frequência por

\ begin {displaymath} \ bgroup \ color {black} E = h \ nu = \ hbar \ omega. \ egroup \ end {displaymath}

Usaremos uma amplitude de probabilidade complexa 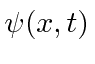\ bgroup \ color {black} $ \ psi (x, t) $ \ egroup para o elétron. As partes reais e imaginárias estão defasadas como os campos EM. A onda progressiva com momentum \ bgroup \ color {black} $ p $ \ egroupe energia, \ bgroup \ color {black} $ E $ \ egroupentão, é

 

\ begin {displaymath} \ bgroup \ color {black} \ psi (x, t) \ propto e ^ {i (kx- \ omega t)} = e ^ {i (px-Et) / \ hbar} \ egroup \ fim {displaymath}

A probabilidade de encontrar um elétron é igual ao quadrado absoluto da amplitude de probabilidade complexa.

 

\ begin {displaymath} \ bgroup \ color {black} P (x, t) = \ vert \ psi (x, t) \ vert ^ 2 \ egroup \ end {displaymath}

 

 

(Superaremos o problema de que essa probabilidade é 1 em todos os lugares para nossa função de onda simples.)

Acabamos de incluir a maior parte da física da Mecânica Quântica. Muito do que fizermos no restante do curso será deduzido do parágrafo acima. Nossa contribuição veio de deBroglie e Plank, com suporte de experimentos.

Vamos resumir a entrada da física novamente.

  • Partículas livres são representadas por funções de onda complexas com uma relação entre suas propriedades de partícula - energia e momento, e suas propriedades de onda - frequência e comprimento de onda dados por Plank e deBroglie.
  • O quadrado absoluto da função de onda fornece a função de distribuição de probabilidade. A mecânica quântica apenas nos diz a probabilidade.
  • Podemos fazer sobreposições de nossas funções de onda de partículas livres para criar estados que não têm momento definido. Veremos que qualquer estado pode ser feito a partir da superposição de estados de partículas livres com diferentes momentos.

Agora temos uma dualidade onda-partícula para todas as partículas; no entanto, a física agora apenas nos diz a probabilidade de ocorrerem alguns eventos quânticos. Perdemos o poder preditivo completo da física clássica.

Gasiorowicz Capítulo 1

Rohlf Capítulo 5

Griffiths 1.2, 1.3

Cohen-Tannoudji et al. Capítulo

 

Derivações e cálculos

Revisão de números complexos

Esta é uma revisão simples, mas você deve certificar-se de usar números complexos corretamente. Um dos erros mais comuns em problemas de teste é esquecer de usar o conjugado complexo ao calcular uma probabilidade.

Um número complexo 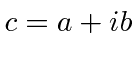\ bgroup \ color {black} $ c = a + ib $ \ egroupconsiste em uma parte real \ bgroup \ color {black} $ a $ \ egroupe uma parte imaginária \ bgroup \ color {black} $ ib $ \ egroup. (Escolhemos \ bgroup \ color {black} $ a $ \ egroupe \ bgroup \ color {black} $ b $ \ egrouppara ser números reais.) \ bgroup \ color {black} $ i $ \ egroupÉ a raiz quadrada de -1.

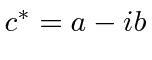O conjugado complexo de \ bgroup \ color {black} $ c $ \ egroupé \ bgroup \ color {black} $ c ^ * = a-ib $ \ egroup. (Basta mudar o sinal de todos os \ bgroup \ color {black} $ i $ \ egroup.)

O quadrado absoluto de um número complexo é calculado multiplicando-o por seu conjugado complexo.

 

\ begin {displaymath} \ bgroup \ color {black} \ vert c \ vert ^ 2 = c ^ * c = (a-ib) (a + ib) = a ^ 2 + iab-iab + b ^ 2 = a ^ 2 + b ^ 2 \ egroup \ end {displaymath}

Isso dá a magnitude ao quadrado do número complexo. O quadrado absoluto é sempre real.

Usaremos exponenciais complexas o tempo todo. 

\ begin {eqnarray *} e ^ {i \ theta} & = & \ cos \ theta + i \ sin \ theta \\ e ^ {- i \ theta} & = & = & \ cos \ theta-i \ sin \ theta \ \ \ end {eqnarray *}

Você pode verificar se o quadrado absoluto dessas exponenciais é sempre 1. Elas costumam ser chamadas de fator de fase.

Podemos escrever e . \ bgroup \ color {black} $ \ sin \ theta = {e ^ {i \ theta} -e ^ {- i \ theta} \ over 2i} $ \ egroup \ bgroup \ color {black} $ \ cos \ theta = {e ^ {i \ theta} + e ^ {- i \ theta} \ over 2} $ \ egroup

Como acontece com outros exponenciais, podemos multiplicá-los adicionando os expoentes.

 

\ begin {displaymath} \ bgroup \ color {black} e ^ {ikx} e ^ {- i \ omega t} = e ^ {i (kx- \ omega t)} \ egroup \ end {displaymath}

Revisão das Ondas Viajantes

Uma onda viajante normal pode ser dada por

 

\ begin {displaymath} \ bgroup \ color {black} \ cos (kx- \ omega t). \ egroup \ end {displaymath}

 

A fase da onda passa \ bgroup \ color {black} $ 2 \ pi $ \ egroupem um comprimento de onda em \ bgroup \ color {black} $ x $ \ egroup. Portanto, o comprimento de onda \ bgroup \ color {black} $ \ lambda $ \ egroupsatisfaz

 

\ begin {displaymath} \ bgroup \ color {black} k \ lambda = 2 \ pi. \ egroup \ end {displaymath}

 

Da mesma forma, a fase passa \ bgroup \ color {black} $ 2 \ pi $ \ egroupem um período \ bgroup \ color {black} $ \ tau $ \ egroupde tempo.

 

\ begin {displaymath} \ bgroup \ color {black} \ omega \ tau = 2 \ pi \ egroup \ end {displaymath}

 

\ bgroup \ color {black} $ \ omega $ \ egroupé a frequência angular. Ele muda a \ bgroup \ color {black} $ 2 \ pi $ \ egroupcada ciclo. A frequência \ bgroup \ color {black} $ \ nu $ \ egroupaumenta em 1 a cada ciclo, então

 

\ begin {displaymath} \ bgroup \ color {black} \ omega = 2 \ pi \ nu. \ egroup \ end {displaymath}

 

Não há razão para memorizar essas equações. Eles devem ser óbvios.

Vamos ver o quão rápido um dos picos da onda se move. Isso é chamado de velocidade de fase. No momento \ bgroup \ color {black} $ t = 0 $ \ egroup, há um pico em \ bgroup \ color {black} $ x = 0 $ \ egroup. Este é o pico para o qual o argumento do cosseno é 0. No momento \ bgroup \ color {black} $ t = 1 $ \ egroup, o argumento é zero quando \ bgroup \ color {black} $ kx = \ omega t $ \ egroupou em . 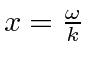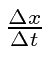Se calcularmos a velocidade de fase tomando , obtemos \ bgroup \ color {black} $ x = {\ omega \ over k} $ \ egroup \ bgroup \ color {black} $ {\ Delta x \ over \ Delta t} $ \ egroup

 

\ begin {displaymath} \ bgroup \ color {black} v _ {\ mathrm {phase}} = {\ omega \ over k}. \ egroup \ end {displaymath}

 

Ou seja, um dos picos dessa onda viaja com velocidade de \ bgroup \ color {black} $ \ omega \ over k $ \ egroup.

 

\ begin {displaymath} \ bgroup \ color {black} v = {\ omega \ over k} = {2 \ pi \ nu \ over {2 \ pi \ over \ lambda}} = \ nu \ lambda \ egroup \ end { displaymath}

 

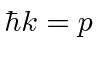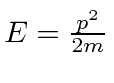
Em QM não-relativista, temos \ bgroup \ color {black} $ \ hbar k = p $ \ egroup, \ bgroup \ color {black} $ E = \ hbar \ omega $ \ egroupe , por isso, \ bgroup \ color {black} $ E = {p ^ 2 \ over 2m} $ \ egroup

 

\ begin {displaymath} \ bgroup \ color {black} \ omega (k) = {E \ over \ hbar} = {\ hbar ^ 2k ^ 2 \ over 2m \ hbar} = {\ hbar k ^ 2 \ over 2m} \ egroup \ end {displaymath}

 

Você deve se lembrar que um pulso se moverá na velocidade do grupo que é dada por

 

\ begin {displaymath} \ bgroup \ color {black} v_g = \ left ({d \ omega \ over dk} \ right) = {2 \ hbar k \ over 2m} = {\ hbar k \ over m} = {p \ over m}. \ egroup \ end {displaymath}

 

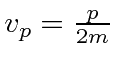
(A velocidade de fase para o caso não relativístico é .) \ bgroup \ color {black} $ v_p = {p \ over 2m} $ \ egroup

Problemas de teste de amostra

  1. Escreva as duas funções de onda de partícula livre (não normalizadas) para uma partícula de energia cinética E. Inclua a dependência de tempo adequada e expressões para outras constantes em termos de E.