Surgimento da Física Moderna

Propriedades gerais do átomo

Discutimos anteriormente a primeira determinação do número de Avogadro, baseada na teoria cinética dos gases. Vimos que esta determinação passa pela estimativa do tamanho do átomo. No exemplo numérico, foi obtido um valor da ordem de 10^-10 m, que podemos adotar como escala típica das dimensões atômicas e moleculares.

Uma vez estabelecido que a matéria é capaz de emitir elétrons, partículas aparentemente puntuais, de carga negativa e de massa muito pequena em comparação com a massa de um átomo, é natural supor que o átomo é composto de um certo número de elétrons e de cargas positivas, de maneira a ser globalmente neutro. A maior parte da massa do átomo deve ser concentrada nas cargas positivas. O tamanho do átomo deve ser da ordem de 10^-10m.

De acordo com a teoria clássica, um campo eletromagnético oscilante induzirá num sistema de cargas, oscilações de freqüência igual à do campo. Se a freqüência do campo for igual a uma freqüência própria de oscilação do sistema, a transferência de energia do campo para o sistema de cargas será particularmente eficiente. Semelhantemente, um sistema de cargas excitado emitirá radiação nas suas freqüências de oscilação. Assim, um modelo do âtomo deveria levar a freqüências de oscilação das cargas nele contidas cujos valores correspondam às linhas de absorção e emissão de radiação pelo elemento em questão.

Modelo de Thomson

Dadas as características acima, a principal hipótese necessária na construção de um modelo atômico diz respeito à distribuição das cargas positivas. J. J. Thomson supús que esta distribuição é contínua e extensa ao tamanho do átomo. Os elétrons seriam cargas negativas puntuais distribuídas neste contínuo de cargas positivas como "passas num pudim".

 

Era então necessário procurar configurações estáveis dos elétrons no contínuo positivo, e determinar as freqüências próprias de oscilação do sistema em torno destas configurações. Os esforços de Thomson no desenvolvimento deste programa não o levaram a resultados animadores.

Espalhamento de partículas a

Em 1896, Henri Becquerel¹ notou manchas sobre placas fotográficas que tinham sido guardadas numa gaveta junto com um pedaço de urânio. Ele tinha assim descoberto - por acaso - a radioatividade. Pouco tempo depois Pierre² e Marie Curie³ observaram radioatividade produzida por outros elementos, em especial tório, polônio e rádio.

Ao estudar a absorçaõ pela matéria da radiação emitida pelo urânio, Rutherford⁴ estabeleceu que ela era composta de dois tipos de raios, que ele denominou raios a e raios b. Rutherford então realizou estudos mais detalhados dos raios a, mostrando que eles são constituídos de partículas carregadas positivamente. Recolhendo uma quantia destas partículas num container evacuado, no qual elas neutralizavam-se, e comprimindo o gás rarefato resultante, pude verificar que este gás apresentava o espectro característico do hélio. Por um procedimento semelhante àquele utilizado por Thomson para os raios catódicos, determinou o valor da razão q_a / m_a. Sabendo o valor da massa (essencialmente igual à do átomo de hélio, m_a = 4 m_H ), estabeleceu que q_a = + 2 e.

Ao realizar estes estudos, Rutherford notou que o ar remanescente na região atravessada pelas partículas produzia algum espalhamento destas. Já que os elétrons são muito mais leves que as partículas a, eles dificilmente podiam ser responsáveis por este efeito. Portanto, Rutherford raciocinou que o estudo sistemático do espalhamento de partículas a poderia fornecer informação valiosa sobre a distribuição da carga positiva no átomo.

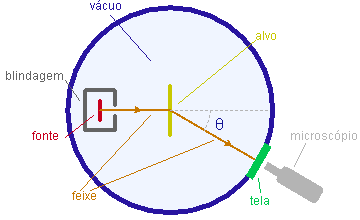
O esquema básico do experimento está representado na figura. Uma fonte raioativa natural emite partículas a que são colimatadas para formar um feixe que se propaga numa câmara evecuada, colidindo com um alvo constituído de uma folha fina de metal. As partículas espalhadas na direção especificada pelo ângulo de espalhamento q são contadas atravês da observação, com um microscópio, das fluorescência que produzem sobre uma tela de sulfeto de zinco.

 

Na base do modelo de Thomson, apenas espalhamentos em pequenos ângulos eram esperados já que, ao penetrar o átomo, a partícula mergulharia suavemente na distribuição contínua de carga, não sofrendo ação violenta. Veja uma animação.

Modelo de Rutherford

Porém, Rutherford observou um número significativo de espalhamentos por grandes ângulos, chegando ocasionalmente a partícula a a "voltar para trás", ou seja, a ser espalhada em ângulos superiores a noventa graus. Para que isto possa acontecer, era necessário que haja dentro do átomo um corpo pesado localizado, capaz de transmitir um forte impulso à partícula.

Rutherford estava sendo levado pelos seus dados a propor o modelo nuclear da átomo, que podemos resumir na afirmação: a carga positiva +Ze está concentrada numa região de tamanho muito menor que o tamanho do átomo, o núcleo do átomo. O núcleo carrega a quase totalidade da massa do átomo, mas o tamanho do átomo é determinado pelo volume ocupado pelos elétrons em movimento orbital ao redor do núcleo.

 

Se o alvo for constituído de um elemento de peso atômico suficientemente alto, uma particula a, ao penetrar profundamente nesta "nuvem eletrônica" e aproximar-se suficientemente do nácleo, sente uma força repulsiva intensa aplicada por um centro de força bem mais pesado que ela e sofre um desvio considerável.

Nestas condições, podemos em boa aproximação desprezar as força aplicadas pelos elétrons sobre a particula a e considerar o núcleo alvo como um centro de força fixo. A força aplicada pelo núcleo sobre a particula é radial e repulsiva, com módulo dado por

(4-1)

onde r é a distância partícula-núcleo e

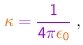(4-2)

sendo e₀ a constante dielétrica do vácuo.

A força (4-1) é conservativa e a energia potencial associada é

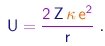(4-3)

A energia mecânica total é conservada e dada por

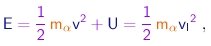(4-4)

onde v_I é a velocidade inicial das partículas, ou seja, antes de elas penetrarem no alvo.

Além desta velocidade, a outra quantidade que pode ser utilizada convenientemente para especificar o estado inicial é o parâmetro de impacto b, que vem a ser a distância entre a linha de movimento inicial da partícula e a linha paralela passando pelo centro de força, ou seja, pelo núcleo do alvo. Vale notar que o momentum angular, que também é conservado já que a força é central, é dado por

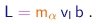(4-5)

A resolução detalhada do problema mostra que a trajetória da partícula é uma hiperbola e estabelece a relação entre o parâmetro de impacto e o ângulo de espalhamento:

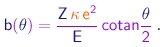(4-6)

 

Vê-se que o ângulo de espalhamento aumenta quando o parâmetro de impacto diminui. Portanto, as partículas espalhadas em ângulos superiores a um dado valor q são aquelas que chegam com parâmetro de impacto inferior a b, dado pela relação (4-6), ou ainda, aquelas cujas linhas de movimento inicial estão contidas num cilindro de seção pb². Denotaremos por I a intensidade do feixe, ou seja, o número de partículas incidentes por unidade de área e tempo. Denotaremos por N₁(>q) o número de partículas espalhadas em ângulos maiores que q, por unidade de tempo e por partícula do alvo. Temos então

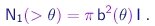(4-7)

Supomos que o alvo é constituído de um único tipo de átomos e denotamos por n o número destes átomos por unidade de volume. Evidentemente, apenas aqueles núcleos que estiverem no caminho do feixe poderão contribuir para o espalhamento. Sendo d a espessura do alvo e S a seção transversal do feixe, haverá n d S tais núcleos espalhadores e o número total de partículas a espalhadas em ângulos maiores que q, por unidade de tempo será

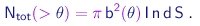(4-8)

Do outro lado, o número de partíclas incidentes, por unidade de tempo, é obviamente

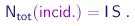(4-9)

Portanto, a fração de partículas espalhadas em ângulos maiores que q é dada por

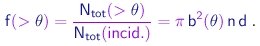(4-10)

Veja um exemplo.

Além da sua variação com o ângulo de espalhamento, fica claro das expressões (4-10) e (4-6) que a quantidade relativa de partículas espalhadas deve possuir as seguintes características, se a teoria estiver correta:

• deve depender da energia E da fonte radioativa, sendo proporcional a E^-2, ou seja, a v_I^-4;
• deve depender do número atômico Z do alvo, sendo proporcional a Z²;
• deve ser proporcional à espessura d do alvo.

Experimentos detalhados realizados por Geiger⁵ e Marsden⁶, colaboradores de Rutherford, confirmaram estas previsões. Vale notar que a análise acima supõe que cada partícula a é espalhada no máximo por um núcleo apenas. Isto sera válido apenas para alvos suficientemente finos. Para alvos mais espessos, correções devidas a espalhamentos múltiplos devem ser levadas em conta.

Tamanho do núcleo atômico

A análise acima supõe que o núcleo pode ser considerado como uma carga pontual, cuja única interação com a partícula a é aquela descrita pela lei de Coulomb. Se a carga positiva contida no átomo estiver na verdade distribuída numa certa região do espaço, e se a partícula a for capaz de penetrar naquela região, desvios entre as predições da teoria e os dados experimentais deverão ser observados. Isto também acontecerá caso outras forças, até aí desconhecidas, entrarem em jogo.

A repulsão eletrostática entre o núcleo e a partícula a mantem esta a uma certa distância mínima r_min do centro do núcleo. Mais especificamente, para uma dada energia total E, a partícula está proibida de penetrar na região na qual a energia potencial U se torna maior que E. A maior aproximação é alcançada quando

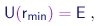(4-11)

ou seja, quando a partícula para e a sua energia cinética se anula. Fica claro que isto só pode ocorrer numa colisão frontal, caracterizada por b = 0 e q = 180^o.

Utilizando a forma (4-3) da energia potencial e resolvendo a equação (4-11), obtemos

(4-12)

Como era de se esperar, para uma dada energia, quanto maior for a carga do núcleo, maior será a distância mínima alcançada pela partícula a. Por esta razão, com as fontes disponíveis na época, não foi possível estabelecer o tamanho dos núcleos dos elementos de grande número atômico - ouro, por exemplo tem Z = 79 - que foram utilizados nos primeiros experimentos. Porém, ao estudar o espalhamento em grandes ângulos por um alvo de número atômico bem menor - alúminio, que tem Z = 13 - foi possível observar desvios dos dados em relação à teoria e estabelecer que a ordem de grandeza do tamanho do núcleo é 10^-15 a 10^-14 metros. Veja um exemplo.

[1] Antoine Henri Becquerel, físico francês, 1852-1908.
[2] Pierre Curie, físico francês, 1859-1906.
[3] Marie Curie, física polonesa, 1867-1934.
[4] Ernest Rutherford, físico neozelandês, 1871-1937.
[5] Hans Geiger, físico alemão, 1882-1947.
[6] Ernest Marsden, físico britânico, 1889-1970.