Surgimento da Física Moderna
Emissão e absorção - Espectros de linhas
- Materiais podem emitir e absorver radiação eletromagnética. Para um dado material em determinadas condições (estado gazoso ou condensado, temperatura, etc), a intensidade de radiação emitida ou absorvida varia com o comprimento de onda l da radiação. Referimo-nos a esta variação como constituindo o espectro de emissão ou absorção do material.
- Um espectro é em geral constituído de várias partes que possuem origens físicas diversas. Mais adiante, discutiremos a parte contínua do espectro associada à agitação térmica dos corpúsculos do material. Nesta seção dirigimos a nossa atenção para a parte discreta do espectro, constituída de linhas de emissão ou absorção que correspondem a valores bem definidos de l. Estas linhas são caracteristicas dos átomos do material e o seu estudo fornece informações valiosas sobre a estrutura destes átomos.
- Uma propriedade importante é que o espectro de linhas de absorção de um dado material é idêntico ao seu espectros de linhas de emissão.
Espectro do átomo de hidrogênio
- Os espectros de linhas dos elementos foram estudados sistematicamente a partir dos últimas décadas do século XIX. Foi verificado que as linhas tendem a se agrupar em séries. As linhas numa dada série tendem a se aproximar cada vez mais quando o comprimento de onda diminui, tendendo para uma determinado valor llim chamado limite da série.
- No caso do hidrogênio - o mais leve dos elementos, portanto presumivelmente o mais simples dos átomos - uma primeira série foi identificada na parte visível do espectro em 1885 por Balmer. Subsequentemente, outras séries foram identificadas, uma no ultravioleta por Lyman e outra no infravermelho por Paschen. Estas três séries estão representadas na figura abaixo (as linhas que estão fora da região visível de espectro estão representadas na cor negra).
- Uma fórmula empírica que descreve com precisão estas séries foi estabelecida por Rydberg e por Ritz. Nela, uma linha é especificada por dois números inteiros. O primeiro m, que pode tomar os valores m=1, m=2, m=3... especifica a series à qual a linha pertence. O segundo n, que pode tomar os valores n=m+1, n=m+2, n=m+3... especifica uma linha dentro da séries. O comprimento de onda da linha (m, n) é dado por
onde a constante de Rydberg tem a valor empírico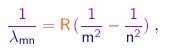
(3-1)
Como a fórmula (3-1) dá o inverso do comprimento de onda, vê-se que qualquer comprimento de onda será dado por uma fração racional multiplicando o inverso da constante de Rydberg, cujo valor é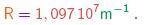
(3-2) 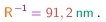
(3-3) - Por exemplo, a primeira linha da série de Balmer corresponde a m=2 e n=3 e possui comprimento de onda igual a
O limite desta série é obtido ao fazer n tender para o infinito e vale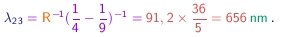
Para a série de Lyman, os valores correspondentes são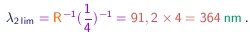
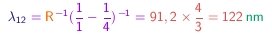
e 

