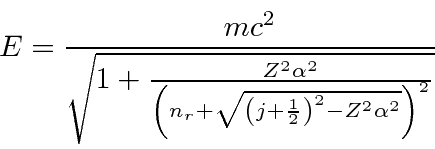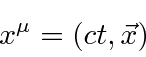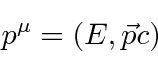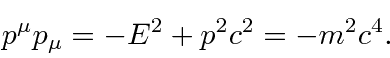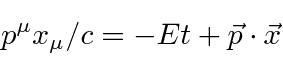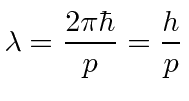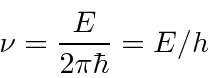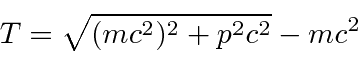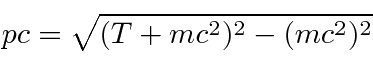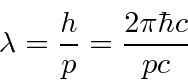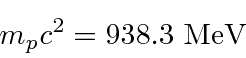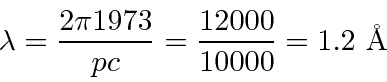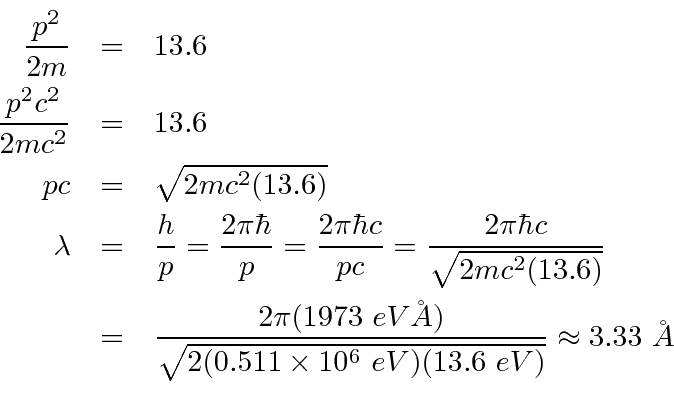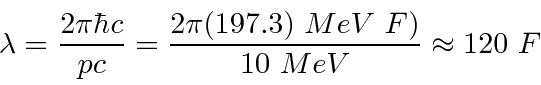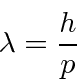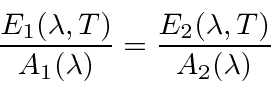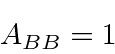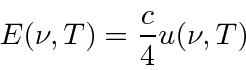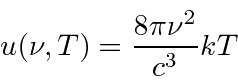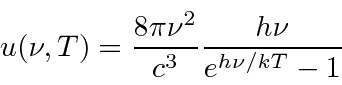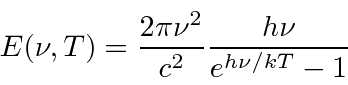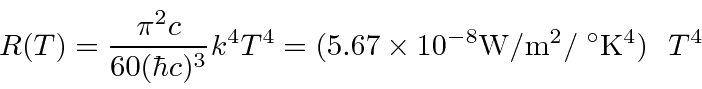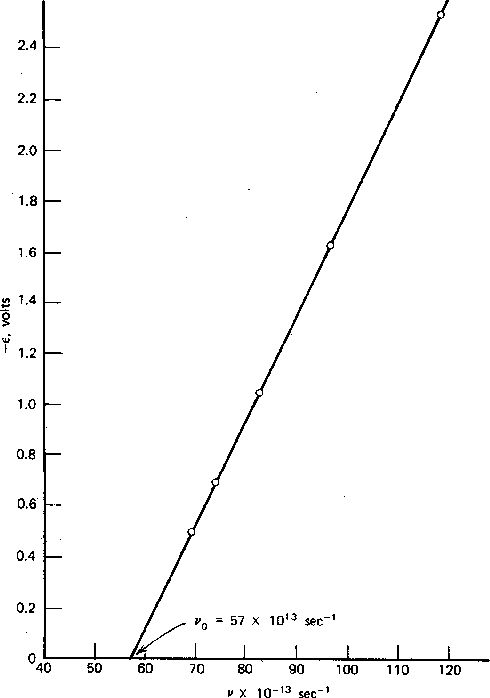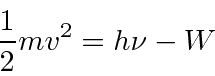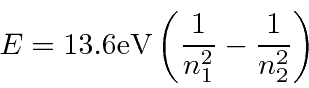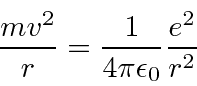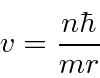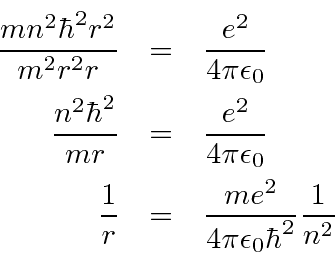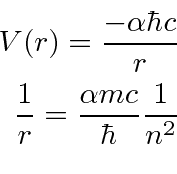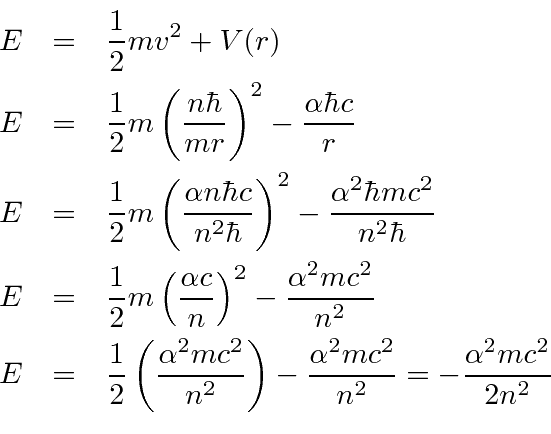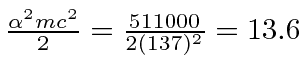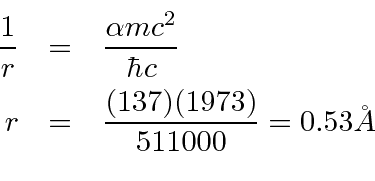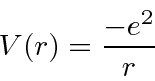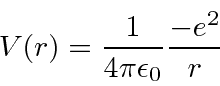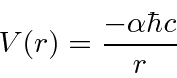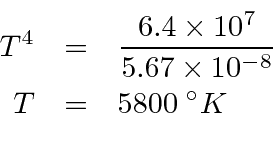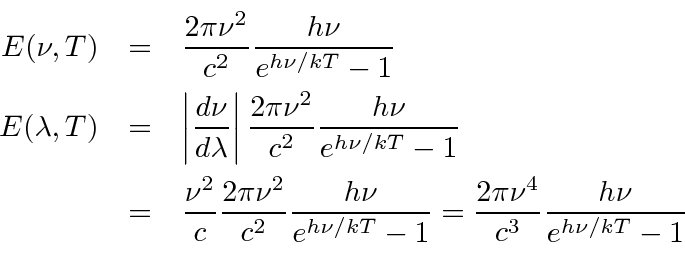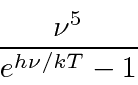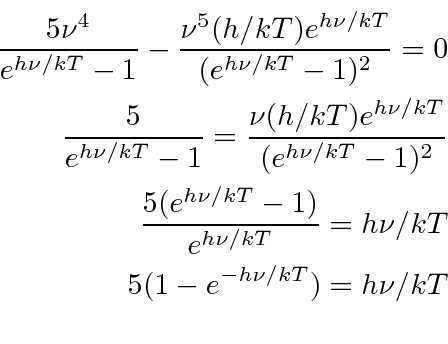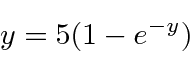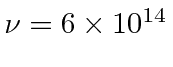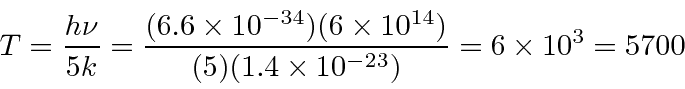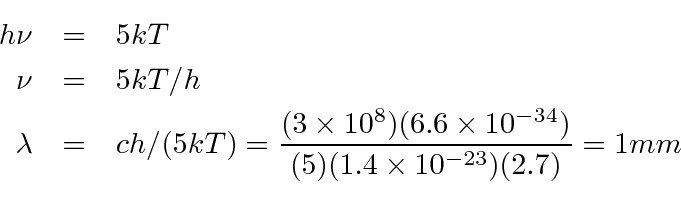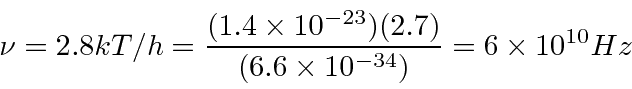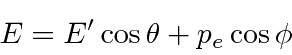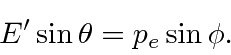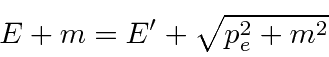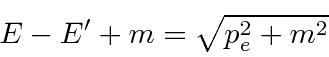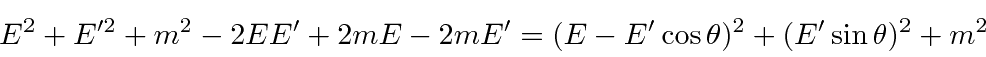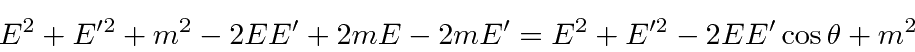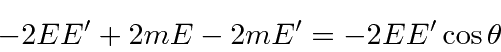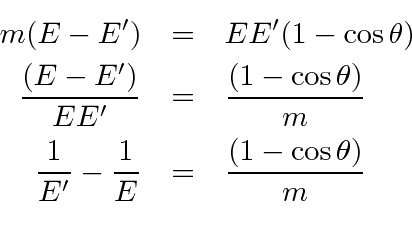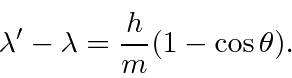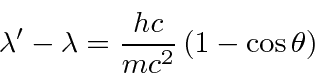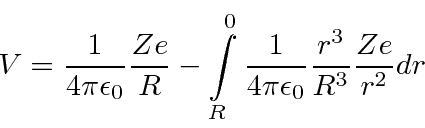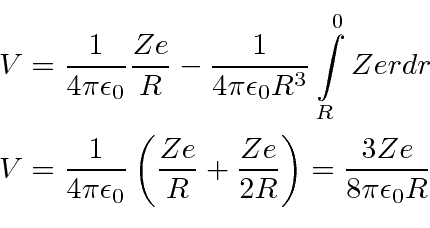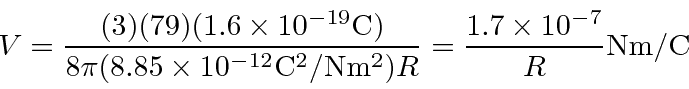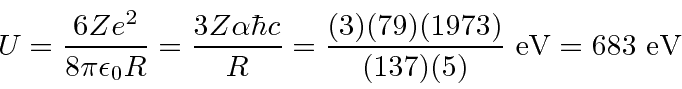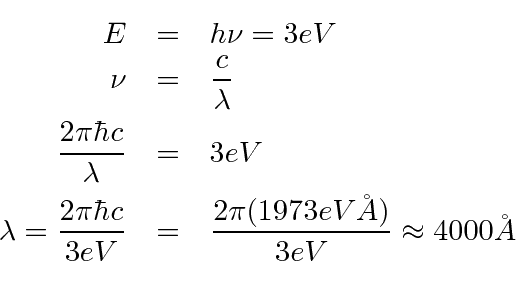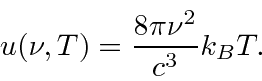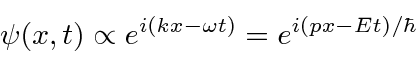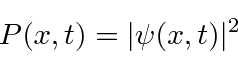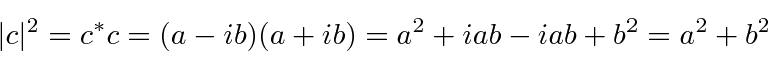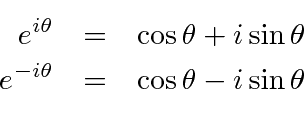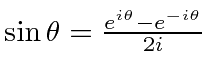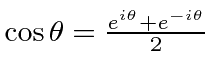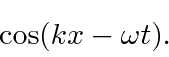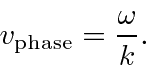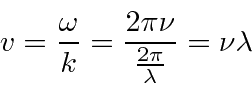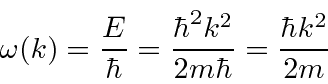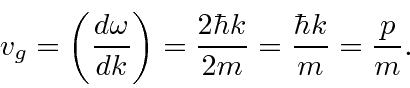Problemas com Física Clássica
Por volta do início do século 20, a física clássica, baseada na mecânica newtoniana e nas equações de eletricidade e magnetismo de Maxwell, descrevia a natureza como a conhecíamos. A Mecânica Estatística também foi uma disciplina bem desenvolvida que descreve sistemas com um grande número de graus de liberdade. Por volta dessa época, Einstein introduziu a Relatividade Especial, que era compatível com as equações de Maxwell, mas mudou nossa compreensão do espaço-tempo e da mecânica modificada.
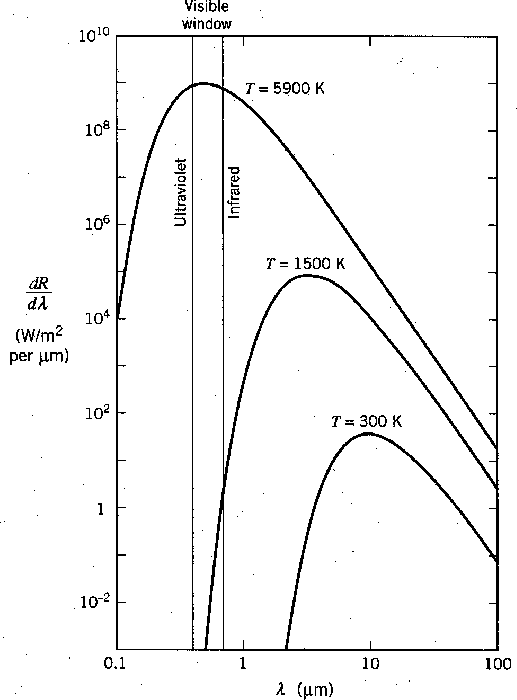
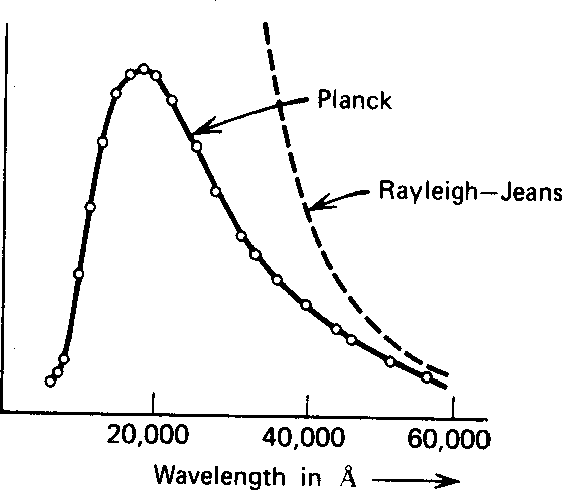
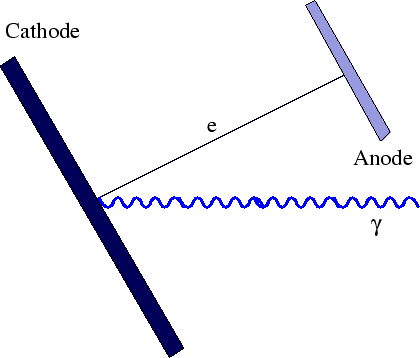
Muitas coisas permaneceram sem explicação. Embora o elétron como constituinte dos átomos tenha sido encontrado, a estrutura atômica era rica e bastante misteriosa. Havia problemas com a física clássica, incluindo a radiação do corpo negro, o efeito fotoelétrico, a teoria atômica básica, a dispersão de Compton e, eventualmente, a difração de todos os tipos de partículas. Plank formulou a hipótese de que a energia EM sempre foi emitida em quanta
para resolver o problema do corpo negro. Muito mais tarde, deBroglie derivou o comprimento de onda das partículas.
No final das contas, os problemas levaram ao desenvolvimento da Mecânica Quântica, em que todas as partículas têm comportamento tanto de onda quanto de partícula.
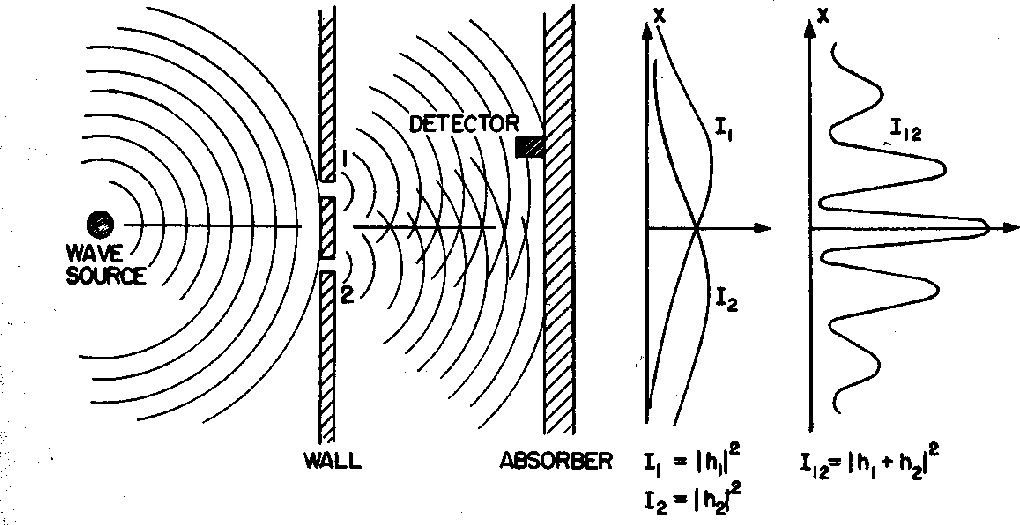
Pensamentos sobre experimentos de difração
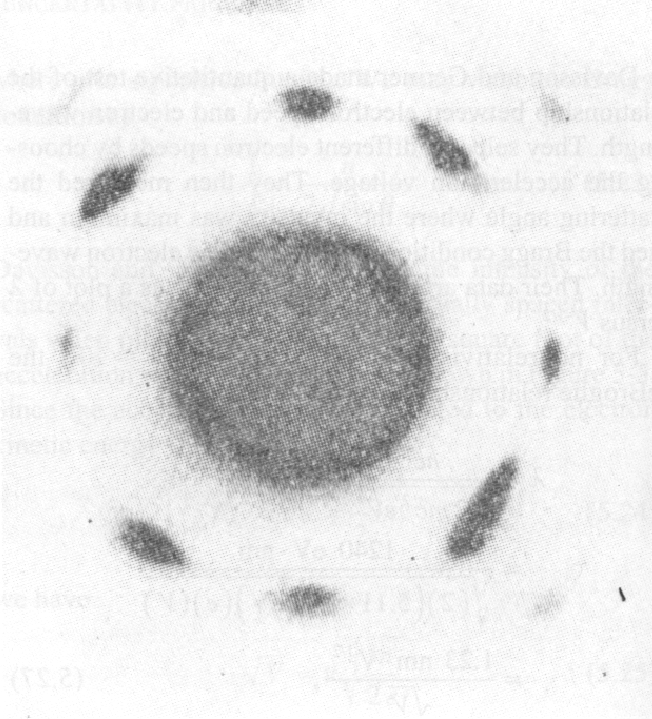
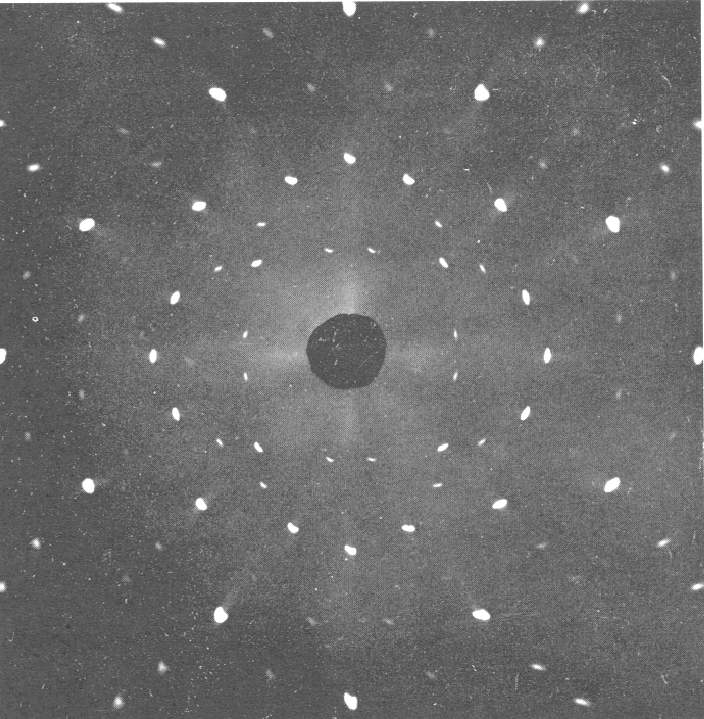
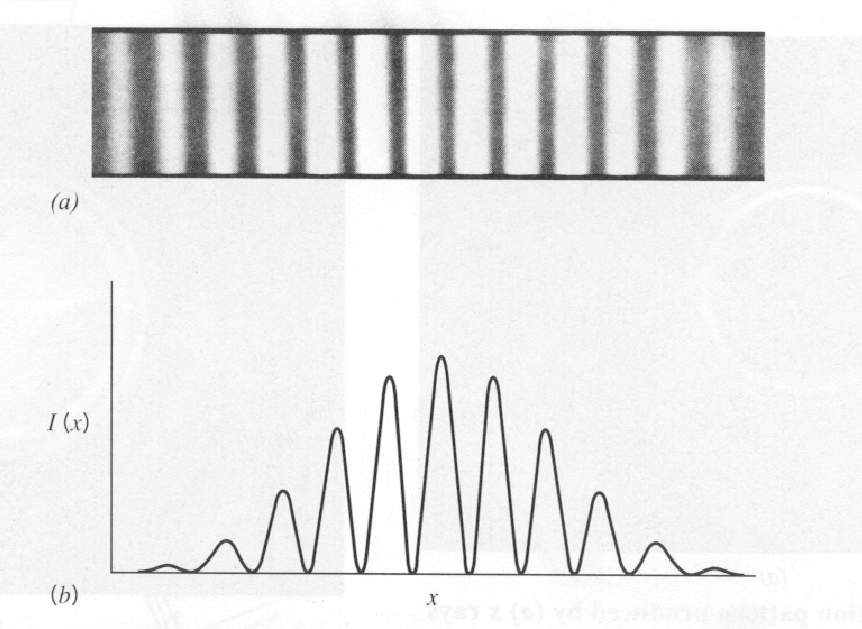
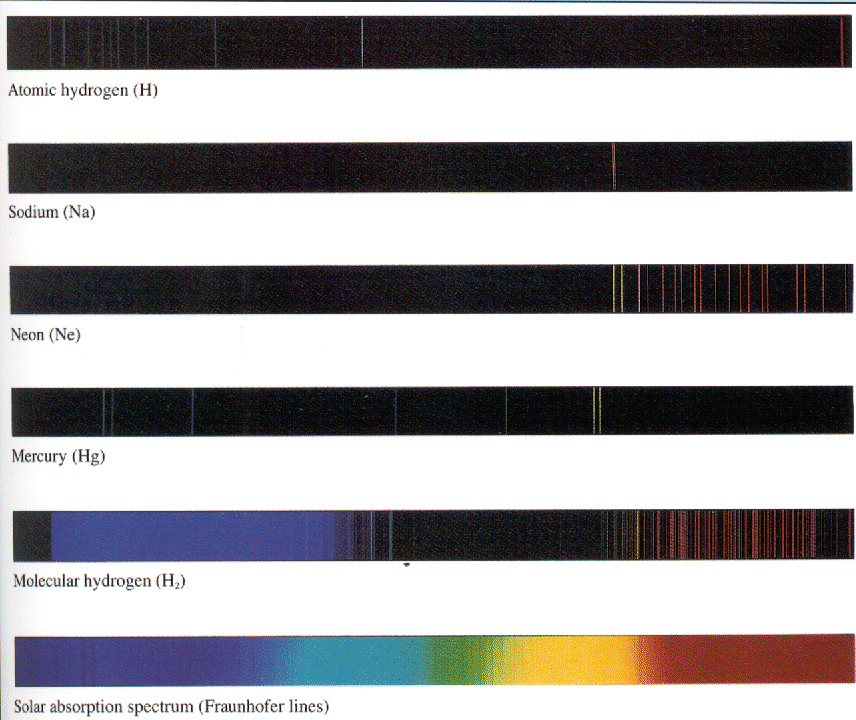
A difração de fótons, elétrons e nêutrons foi observada e usada para estudar a estrutura cristalina.
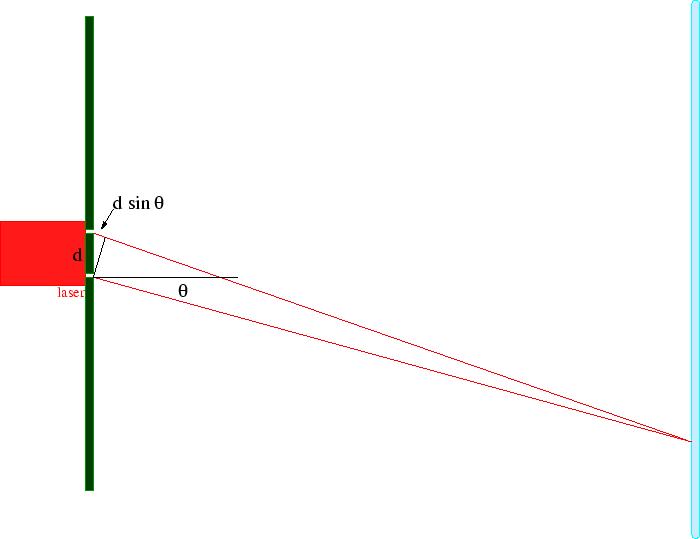
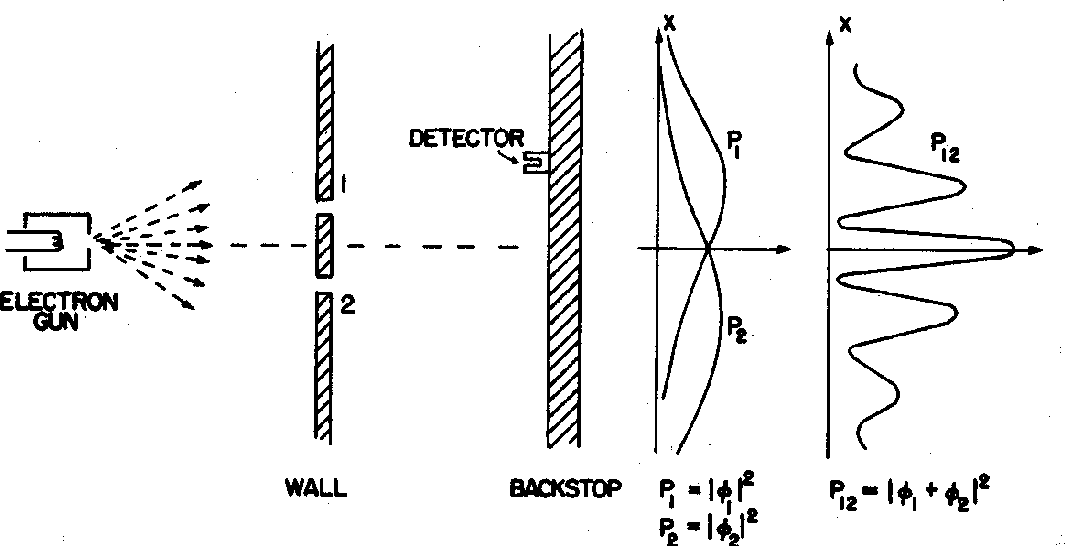
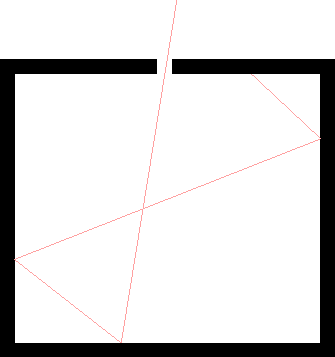
Para entender a entrada experimental de uma forma simplificada, consideramos alguns experimentos mentais sobre a difração de fótons, elétrons e balas através de duas fendas. Por exemplo, os fótons, que compõem todas as ondas eletromagnéticas, mostram um padrão de difração exatamente como previsto pela teoria de ondas eletromagnéticas, mas sempre detectamos um número inteiro de fótons com a relação de Plank,
satisfazendo entre a freqüência das ondas e a energia das partículas.
Elétrons, nêutrons e tudo o mais se comportam exatamente da mesma maneira, exibindo difração em forma de onda, mas detectando e satisfazendo um número inteiro de partículas. Esta fórmula de comprimento de onda deBroglie relaciona a propriedade da onda à propriedade da partícula.
Amplitudes de probabilidade
Na Mecânica Quântica, entendemos essa dualidade onda-partícula usando amplitudes de probabilidade (complexas) que satisfazem uma equação de onda.
A probabilidade de encontrar uma partícula em uma posição ![]() em algum momento
em algum momento ![]() é o quadrado absoluto da amplitude da probabilidade.
é o quadrado absoluto da amplitude da probabilidade.
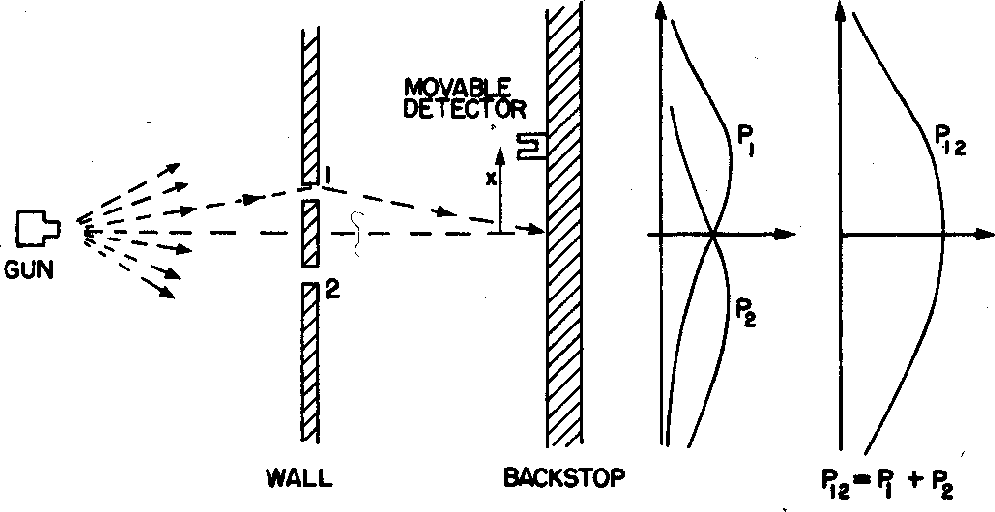
Para calcular a probabilidade de encontrar um elétron em nosso detector de experimento mental adicionamos, à amplitude da probabilidade de chegar ao detector pela fenda 1, a amplitude de chegar ao detector pela fenda 2 e obter o quadrado absoluto.
A Mecânica Quântica muda completamente nossa visão do mundo. Em vez de um mundo determinístico, agora temos apenas probabilidades . Não podemos nem mesmo medir a posição e o momento de uma partícula (com precisão) ao mesmo tempo. A mecânica quântica exigirá que usemos a matemática de operadores, transformadas de Fourier, espaços vetoriais e muito mais.
Pacotes de onda e incerteza
A amplitude de probabilidade para uma partícula livre com momento ![]() e energia é a função de onda complexa
e energia é a função de onda complexa
Observe que em 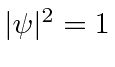 todos os lugares isso não representa uma partícula localizada. Na verdade, reconhecemos na propriedade de onda que, para termos exatamente uma frequência, uma onda deve ser espalhada no espaço.
todos os lugares isso não representa uma partícula localizada. Na verdade, reconhecemos na propriedade de onda que, para termos exatamente uma frequência, uma onda deve ser espalhada no espaço.
Podemos construir pacotes de ondas localizados que representam partículas individuais somando essas funções de onda de partículas livres (com alguns coeficientes).
(Mudamos para uma dimensão para simplificar.) Da mesma forma, podemos calcular o coeficiente para cada momento
Esses coeficientes  são na verdade a função de estado da partícula no espaço de momento. Podemos descrever o estado de uma partícula em espaço de posição com
são na verdade a função de estado da partícula no espaço de momento. Podemos descrever o estado de uma partícula em espaço de posição com  ou em espaço de momento com
ou em espaço de momento com 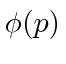 .
.
Podemos usar 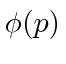 para calcular a função de distribuição de probabilidade para o momento.
para calcular a função de distribuição de probabilidade para o momento.
Mostraremos que pacotes de ondas como esses se comportam corretamente no limite clássico, justificando a escolha que fizemos.
O Princípio da Incerteza de Heisenberg é uma propriedade das ondas que podemos deduzir de nosso estudo de pacotes de ondas localizados.
Isso mostra que, devido à natureza ondulatória das partículas, não podemos localizar uma partícula em um pequeno volume sem aumentar sua energia. Por exemplo, podemos estimar a energia do estado fundamental (e o tamanho) de um átomo de hidrogênio muito bem a partir do princípio da incerteza.
O próximo passo na construção da Mecânica Quântica é determinar como uma função de onda se desenvolve com o tempo - particularmente útil se um potencial for aplicado. A equação diferencial que as funções de onda devem satisfazer é chamada de Equação de Schrödinger.
Operadores
A Equação de Schrödinger vem diretamente de nossa compreensão dos pacotes de ondas. Para passar de pacotes de ondas a uma equação diferencial, usamos o novo conceito de operadores (lineares).
Determinamos os operadores de momento e energia requerendo que, quando um operador de alguma variável ![]() venha a atuar em nossa função de onda simples, obtenhamos
venha a atuar em nossa função de onda simples, obtenhamos ![]() vezes a mesma função de onda.
vezes a mesma função de onda.
Expectativas de valores
Podemos usar operadores para nos ajudar a calcular o valor esperado de uma variável física. Se uma partícula está no estado 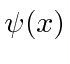 , a maneira normal de calcular o valor esperado de
, a maneira normal de calcular o valor esperado de é
é
Se valor esperado da variável que desejamos calcular não for o de uma função simples de ![]() (como
(como ![]() ) , deixe o operador
) , deixe o operador 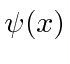 atuar
atuar
Temos uma notação abreviada para o valor esperado de uma variável ![]() no estado
no estado ![]() que é bastante útil.
que é bastante útil.
Estendemos a notação de apenas valores de expectativa para
e
Usamos muito essa notação abreviada de Dirac Bra-Ket .
Comutadores
Operadores (ou variáveis na mecânica quântica) não necessariamente comutam. Podemos calcular o comutador de duas variáveis, por exemplo
Mais tarde, aprenderemos a derivar a relação de incerteza para duas variáveis de seu comutador. Também usaremos comutadores para resolver vários problemas importantes.
A Equação de Schrödinger
As funções de onda devem satisfazer a equação de Schrödinger, que na verdade é uma equação de onda.
Nós o usaremos para resolver muitos problemas neste curso. Em termos de operadores, isso pode ser escrito como
é o operador hamiltoniano. Portanto, a Equação de Schrödinger é, em certo sentido, simplesmente a afirmação (nos operadores) de que a energia cinética mais a energia potencial é igual à energia total.
Autofunções, autovalores e espaços vetoriais
Para qualquer problema físico, as soluções da equação de Schrödinger separadas (entre tempo e espaço)
formam um conjunto extremamente importante. Se assumirmos que a equação se separa, obtemos as duas equações (em uma dimensão para simplificar)
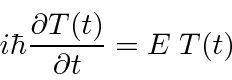
A segunda equação é chamada de equação de Schrödinger independente do tempo. Para estados ligados, existem apenas soluções para essa equação para algum conjunto quantizado de energias
Para estados que não são limitados, é permitida uma faixa contínua de energia.
A equação de Schrödinger independente do tempo é um exemplo de uma equação de autovalor.
Se operarmos ![]() com
com ![]() , obteremos a mesma função
, obteremos a mesma função ![]() vezes alguma constante. Nesse caso,
vezes alguma constante. Nesse caso, ![]() seria chamada de função autônoma e
seria chamada de função autônoma e ![]() seria chamada de autovalor. Normalmente, há um número infinito de soluções, indicado pelo índice
seria chamada de autovalor. Normalmente, há um número infinito de soluções, indicado pelo índice ![]() aqui.
aqui.
Os operadores para variáveis físicas devem ter autovalores reais. Eles são chamados de operadores hermitianos. Podemos mostrar que as autofunções dos operadores Hermitianos são ortogonais (e podem ser normalizadas).
(No caso de autofunções com o mesmo autovalor, chamadas autofunções degeneradas, podemos escolher combinações lineares ortogonais entre si.) Vamos assumir que as autofunções também formam um conjunto completo de modo que qualquer função de onda possa ser expandida nelas
onde ![]() são coeficientes que podem ser facilmente calculados (devido à ortonormalidade) por
são coeficientes que podem ser facilmente calculados (devido à ortonormalidade) por
Portanto, agora temos outra maneira de representar um estado (além de espaço de posição e espaço de momento). Podemos representar um estado fornecendo os coeficientes em soma acima. (Observe que é apenas uma autofunção do operador momentum e é apenas uma autofunção do operador de posição (no espaço p), portanto, eles também representam uma expansão do estado em termos de autofunções.)
Como a ![]() forma é um conjunto ortonormal completo, eles podem ser considerados como vetores unitários de um espaço vetorial. A função de onda arbitrária
forma é um conjunto ortonormal completo, eles podem ser considerados como vetores unitários de um espaço vetorial. A função de onda arbitrária ![]() seria um vetor naquele espaço e poderia ser representada por seus coeficientes.
seria um vetor naquele espaço e poderia ser representada por seus coeficientes.
O bra-ket pode ser pensado como um produto escalar entre o vetor arbitrário e um dos vetores unitários. Podemos usar a expansão em termos de estados próprios de energia para calcular muitas coisas. Em particular, uma vez que o tempo de desenvolvimento dos estados próprios de energia é muito simples,
podemos usar esses estados próprios para acompanhar o desenvolvimento de um estado arbitrário no tempo ![]()
simplesmente calculando os coeficientes ![]() em
em ![]() .
.
Podemos definir o conjugado hermitiano ![]() do operador
do operador ![]() por
por
Os operadores hermitianos ![]() têm essa propriedade em que
têm essa propriedade em que![]() .
.
Uma partícula em uma caixa
Como uma ilustração concreta dessas idéias, estudamos a partícula em uma caixa (em uma dimensão). Esta é apenas uma partícula (de massa ![]() ) que é livre para se mover dentro das paredes de uma caixa
) que é livre para se mover dentro das paredes de uma caixa 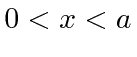 , mas que não pode penetrar nas paredes. Representamos isso por um potencial que é zero dentro da caixa e infinito fora. Resolvemos a equação de Schrödinger dentro da caixa e percebemos que a probabilidade de a partícula estar fora da caixa e, portanto, a função de onda lá, deve ser zero. Uma vez que não há potencial dentro, a equação de Schrödinger é
, mas que não pode penetrar nas paredes. Representamos isso por um potencial que é zero dentro da caixa e infinito fora. Resolvemos a equação de Schrödinger dentro da caixa e percebemos que a probabilidade de a partícula estar fora da caixa e, portanto, a função de onda lá, deve ser zero. Uma vez que não há potencial dentro, a equação de Schrödinger é
onde previmos que haverão muitas soluções indexadas por ![]() . Conhecemos quatro funções (apenas 2 linearmente independentes) que têm um segundo derivado que é uma constante vezes a mesma função:
. Conhecemos quatro funções (apenas 2 linearmente independentes) que têm um segundo derivado que é uma constante vezes a mesma função:
A função de onda deve ser contínua, portanto necessitamos das condições de contorno
A função seno é sempre zero em ![]() e nenhuma das outras é. Para tornar a função seno zero em
e nenhuma das outras é. Para tornar a função seno zero em ![]() precisamos
precisamos ![]() ou
ou 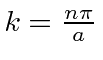 . Assim, as autofunções de energia são dadas por
. Assim, as autofunções de energia são dadas por
onde permitimos a constante geral ![]() porque satisfaz à equação diferencial. Voltando a
porque satisfaz à equação diferencial. Voltando a 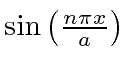 na equação de Schrödinger, descobrimos que
na equação de Schrödinger, descobrimos que
Somente energias quantizadas são permitidas quando resolvemos este problema de estado limitado. Temos uma tarefa restante. Os estados próprios devem ser normalizados para representar uma partícula.
Portanto, a função de onda será normalizada se escolhermos
Sempre podemos multiplicar por qualquer número complexo de magnitude 1, mas isso não muda a física. Este exemplo mostra muitos dos recursos que veremos para outros problemas de estado vinculado. A única diferença é que, por causa de uma mudança infinita no potencial nas paredes da caixa, não precisamos manter a primeira derivada da função de onda contínua. Em todos os outros problemas, teremos que prestar mais atenção a isso.
Potenciais constantes por partes em uma dimensão
Agora estudamos a física de vários potenciais simples em uma dimensão . Primeiro, uma série de potenciais constantes por partes para os quais a equação de Schrödinger é
ou
e a solução geral , para 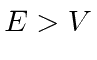 , pode ser escrita como
, pode ser escrita como
ou
com
Também precisaremos de soluções para as regiões classicamente proibidas, onde a energia total é menor do que a energia potencial.
com
(Ambos ![]() e
e ![]() são números reais positivos.) Os problemas de espalhamento 1D costumam ser análogos aos problemas em que a luz é refletida ou transmitida na superfície do vidro.
são números reais positivos.) Os problemas de espalhamento 1D costumam ser análogos aos problemas em que a luz é refletida ou transmitida na superfície do vidro.
Em primeiro lugar, calcula-se a probabilidade da partícula de energia ![]() refletir-se por um passo de potencial de altura
refletir-se por um passo de potencial de altura
Também usamos este exemplo para entender a probabilidade atual.
Em segundo lugar, investigamos o poço de potencial quadrado do poço de potencial quadrado ( 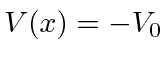 para
para 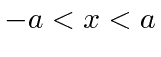 e
e 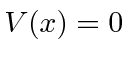 em outros lugares), para o caso em que a partícula não está ligada
em outros lugares), para o caso em que a partícula não está ligada 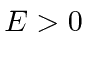 . Assumindo um feixe de partículas incidente da esquerda, precisamos combinar as soluções nas três regiões nos limites em
. Assumindo um feixe de partículas incidente da esquerda, precisamos combinar as soluções nas três regiões nos limites em 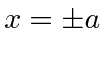 . Depois de alguma aritmética difícil, as probabilidades de serem transmitidas ou refletidas são calculadas. Verifica-se que a probabilidade de ser transmitido vai para 1 para algumas energias particulares.
. Depois de alguma aritmética difícil, as probabilidades de serem transmitidas ou refletidas são calculadas. Verifica-se que a probabilidade de ser transmitido vai para 1 para algumas energias particulares.
Este tipo de comportamento é exibido pelo espalhamento de elétrons dos átomos. Em algumas energias, a probabilidade de espalhamento vai para zero.
Terceiro, estudamos a barreira de potencial quadrada ( 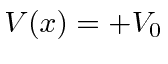 para
para 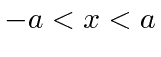 e
e 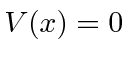 em outro lugar), para o caso em que
em outro lugar), para o caso em que 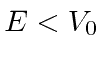 . Classicamente a probabilidade de ser transmitida seria zero, uma vez que a partícula é excluída energeticamente de estar dentro da barreira. O cálculo quântico dá a probabilidade de ser transmitido através da barreira como
. Classicamente a probabilidade de ser transmitida seria zero, uma vez que a partícula é excluída energeticamente de estar dentro da barreira. O cálculo quântico dá a probabilidade de ser transmitido através da barreira como
onde
O estudo desta expressão mostra que a probabilidade de ser transmitido diminui à medida que a barreira fica mais alta ou mais larga. No entanto, a penetração da barreira é um fenômeno quântico importante.
Também estudamos bem o quadrado para o caso de estado ligado em que 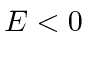 . Aqui, precisamos resolver uma equação transcendental para determinar as energias do estado vinculado. O número de estados vinculados aumenta com a profundidade e a largura do poço, mas sempre há pelo menos um estado vinculado.
. Aqui, precisamos resolver uma equação transcendental para determinar as energias do estado vinculado. O número de estados vinculados aumenta com a profundidade e a largura do poço, mas sempre há pelo menos um estado vinculado.
O oscilador harmônico em uma dimensão
Em seguida, resolvemos os autoestados de energia do potencial do oscilador harmônico , onde eliminamos a constante da mola usando a frequência clássica do oscilador . Os valores próprios de energia são
Os autoestados de energia acabam sendo um polinômio (em![]() ) de
) de ![]() tempos de grau . Portanto, o estado fundamental, devidamente normalizado, é de apenas
tempos de grau . Portanto, o estado fundamental, devidamente normalizado, é de apenas ![]()
Posteriormente, retornaremos o oscilador harmônico para resolver o problema pelos métodos do operador.
Potenciais de função delta em uma dimensão
O potencial de função delta é muito útil para fazer modelos simples de moléculas e sólidos. Primeiro, resolvemos o problema com uma função delta atrativa
Como o estado ligado tem energia negativa, as soluções normalizáveis são![]() para
para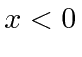 e
e ![]() para
para 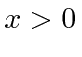 . Tornar
. Tornar 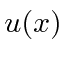 contínuo e sua primeira derivada ter uma descontinuidade calculada a partir da equação de Schrödinger em
contínuo e sua primeira derivada ter uma descontinuidade calculada a partir da equação de Schrödinger em ![]() , nos dá exatamente um estado ligado com
, nos dá exatamente um estado ligado com
Em seguida, usamos duas funções delta para modelar uma molécula. Resolvendo esse problema combinando funções de onda nas fronteiras em ![]() , encontramos novamente equações transcendentais para duas energias de estado vinculadas. A energia do estado fundamental é mais negativa do que para uma função delta, indicando que a molécula seria ligada. Uma olhada na função de onda mostra que as duas funções delta podem diminuir a energia cinética em comparação com o estado de uma função delta, reduzindo a curvatura da função de onda. O estado excitado tem mais curvatura do que o estado atômico, então não esperaríamos ligações moleculares nesse estado.
, encontramos novamente equações transcendentais para duas energias de estado vinculadas. A energia do estado fundamental é mais negativa do que para uma função delta, indicando que a molécula seria ligada. Uma olhada na função de onda mostra que as duas funções delta podem diminuir a energia cinética em comparação com o estado de uma função delta, reduzindo a curvatura da função de onda. O estado excitado tem mais curvatura do que o estado atômico, então não esperaríamos ligações moleculares nesse estado.
Nosso potencial 1D final é o modelo de um sólido.
Isso tem uma matriz periódica infinita de funções delta, então isso pode ser aplicável a um cristal. A solução para isso é um pouco complicada, mas se resume a
Como o lado direito da equação pode ser maior que 1,0 (ou menor que -1), existem regiões para as quais não há soluções. Também existem faixas de energias com soluções. Essas faixas de energia são vistas em cristais (como Si).
Solução de oscilador harmônico com operadores
Podemos resolver o problema do oscilador harmônico usando métodos de operadores. Escrevemos o hamiltoniano em termos do operador
Calculamos os comutadores
Se aplicamos o comutador ![\ bgroup \ color {black} $ [H, A] $ \ egroup](https://quantummechanics.ucsd.edu/ph130a/130_notes/img182.png) à autofunção
à autofunção ![]() , obtemos
, obtemos![\ bgroup \ color {black} $ [H, A] u_n = - \ hbar \ omega Au_n $ \ egroup](https://quantummechanics.ucsd.edu/ph130a/130_notes/img184.png) o qual rearranja a equação de autovalor
o qual rearranja a equação de autovalor
Isso diz que 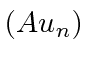 é uma autofunção de
é uma autofunção de ![]() com autovalor
com autovalor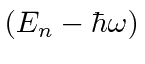 , portanto, reduz a energia em
, portanto, reduz a energia em ![]() . Uma vez que a energia deve ser positiva para este hamiltoniano, a redução deve parar em algum lugar, no estado fundamental, onde teremos
. Uma vez que a energia deve ser positiva para este hamiltoniano, a redução deve parar em algum lugar, no estado fundamental, onde teremos
Isso nos permite calcular a energia do estado fundamental como
mostrando que a energia do estado fundamental é 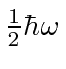 . Da mesma forma,
. Da mesma forma, ![]() aumenta a energia em
aumenta a energia em ![]() . Podemos subir e descer a escada de energia usando
. Podemos subir e descer a escada de energia usando![]() e
e![]() , sempre em etapas de
, sempre em etapas de![]() . Os valores próprios de energia são, portanto,
. Os valores próprios de energia são, portanto,
Um pouco mais de cálculos mostra que
e
Essas fórmulas são úteis para todos os tipos de cálculos dentro do importante sistema oscilador harmônico. Ambos ![]() e
e ![]() podem ser escritos em termos de
podem ser escritos em termos de ![]() e
e ![]() .
.
Mais diversão com os operadores
Encontramos o operador de desenvolvimento de tempo resolvendo a equação .
Isso implica que ![]() é o operador de desenvolvimento de tempo. Em alguns casos, podemos calcular o operador real da série de potências para o exponencial.
é o operador de desenvolvimento de tempo. Em alguns casos, podemos calcular o operador real da série de potências para o exponencial.
Temos trabalhado no que é chamado de quadro de Schrödinger, no qual as funções de onda (ou estados) se desenvolvem com o tempo. Existe a imagem alternativa de Heisenberg em que os operadores se desenvolvem com o tempo enquanto os estados não mudam.
Por exemplo, se quisermos calcular o valor esperado do operador ![]() como uma função do tempo na imagem de Schrödinger usual, obtemos
como uma função do tempo na imagem de Schrödinger usual, obtemos
No quadro de Heisenberg, o operador
Usamos métodos de operação para calcular a relação de incerteza entre as variáveis não comutáveis
o que dá o resultado que deduzimos dos pacotes de ondas para ![]() e
e ![]() .
.
Novamente, usamos métodos de operador para calcular a derivada de tempo de um valor esperado.
(A maioria dos operadores que usamos não tem dependência de tempo explícita, então o segundo termo geralmente é zero.) Isso novamente mostra a importância do operador hamiltoniano para o desenvolvimento do tempo. Podemos usar isso para mostrar que na mecânica quântica os valores esperados ![]() e
e ![]() se comportam como esperaríamos da mecânica newtoniana (teorema de Ehrenfest) .
se comportam como esperaríamos da mecânica newtoniana (teorema de Ehrenfest) .
Qualquer operador ![]() que comuta com o hamiltoniano tem um valor de expectativa independente do tempo . As autofunções de energia também podem ser autofunções (simultâneas) do operador de comutação
que comuta com o hamiltoniano tem um valor de expectativa independente do tempo . As autofunções de energia também podem ser autofunções (simultâneas) do operador de comutação ![]() . Geralmente é uma simetria do
. Geralmente é uma simetria do ![]() que leva a um operador de comutação e, portanto, uma constante adicional do movimento.
que leva a um operador de comutação e, portanto, uma constante adicional do movimento.
Duas partículas em 3 dimensões
Até agora, trabalhamos com estados de apenas uma partícula em uma dimensão. A extensão para duas partículas diferentes e para três dimensões é direta. As coordenadas e os momentos de diferentes partículas e das dimensões adicionais comutam entre si como poderíamos esperar da física clássica. As únicas coisas que não comutam são uma coordenada com seu impulso, por exemplo.
enquanto
Podemos escrever estados para duas partículas que não estão correlacionadas, como 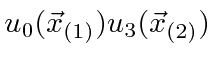 , ou podemos escrever estados em que as partículas estão correlacionadas. O hamiltoniano para duas partículas em 3 dimensões simplesmente se torna
, ou podemos escrever estados em que as partículas estão correlacionadas. O hamiltoniano para duas partículas em 3 dimensões simplesmente se torna
Se duas partículas interagem entre si, sem potencial externo,
o hamiltoniano tem uma simetria translacional e permanece invariante sob a tradução . Podemos mostrar que esta simetria translacional implica na conservação do momento total . Da mesma forma, mostraremos que a simetria rotacional implica na conservação do momento angular e que a simetria do tempo implica na conservação da energia. 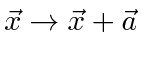
Para duas partículas interagindo através de um potencial que depende apenas da diferença nas coordenadas,
podemos fazer a transformação usual para o centro de massa feita na mecânica clássica
e reduzir o problema para o CM se movendo como uma partícula livre
mais um problema potencial em 3 dimensões com a massa reduzida usual.
Portanto, agora temos um problema 3D para resolver (3 variáveis em vez de 6).
Partículas Idênticas
Partículas idênticas nos apresentam outra simetria na natureza. Os elétrons, por exemplo, são indistinguíveis uns dos outros, então devemos ter uma simetria do hamiltoniano sob o intercâmbio de qualquer par de elétrons. Vamos chamar a operadora que intercambia elétron-1 e elétron-2 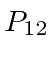
Portanto, podemos fazer com que nossos estados próprios de energia também sejam estados próprios de 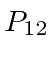 . É fácil ver (operando em um estado próprio duas vezes com
. É fácil ver (operando em um estado próprio duas vezes com 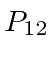 ) que os valores próprios possíveis são
) que os valores próprios possíveis são ![]() . É uma lei da física que
. É uma lei da física que ![]() partículas de spin chamadas férmions (como elétrons) sempre são antissimétricas em intercâmbio , enquanto partículas com spin inteiro chamadas de bósons (como fótons) sempre são simétricas em intercâmbio . A anti-simetria sob intercâmbio leva ao princípio de exclusão de Pauli de que dois elétrons (por exemplo) não podem estar no mesmo estado.
partículas de spin chamadas férmions (como elétrons) sempre são antissimétricas em intercâmbio , enquanto partículas com spin inteiro chamadas de bósons (como fótons) sempre são simétricas em intercâmbio . A anti-simetria sob intercâmbio leva ao princípio de exclusão de Pauli de que dois elétrons (por exemplo) não podem estar no mesmo estado.
Alguns problemas 3D separáveis em coordenadas cartesianas
Começamos nosso estudo da Mecânica Quântica em 3 dimensões com alguns casos simples de problemas que podem ser separados em coordenadas cartesianas. Isso é possível quando o hamiltoniano pode ser escrito
Um bom exemplo de separação de variável em coordenadas cartesianas é o oscilador harmônico 3D
que tem energias que dependem de três números quânticos.
Ele realmente se comporta como 3 osciladores harmônicos unidimensionais independentes.
Outro problema que separa é a partícula em uma caixa 3D . Novamente, as energias dependem de três números quânticos
para uma caixa cúbica de lado ![]() . Investigamos o efeito do princípio de exclusão de Pauli preenchendo nossa caixa 3D com férmions idênticos, que devem estar todos em estados diferentes. Podemos usar isso para modelar anãs brancas ou estrelas de nêutrons.
. Investigamos o efeito do princípio de exclusão de Pauli preenchendo nossa caixa 3D com férmions idênticos, que devem estar todos em estados diferentes. Podemos usar isso para modelar anãs brancas ou estrelas de nêutrons.
Na física clássica, são necessárias três coordenadas para fornecer a localização de uma partícula em 3D. Na mecânica quântica, estamos descobrindo que são necessários três números quânticos para rotular e autoestar de energia (sem incluir o spin).
Momentum Angular
Para o comum problema de potenciais centrais 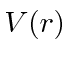 , usamos o óbvio simetria rotacional ao descobrir que o momento angular , , operadores comutar com ,
, usamos o óbvio simetria rotacional ao descobrir que o momento angular , , operadores comutar com , 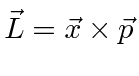
![]()
mas eles não se deslocam entre si.
Queremos encontrar dois operadores mutuamente comutantes que comutam com ![]() , então voltamos para
, então voltamos para 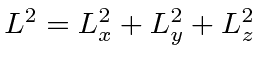 o qual comuta com cada componente de
o qual comuta com cada componente de ![]() .
.
Escolhemos nossos dois operadores para serem ![]() e
e ![]() .
.
Alguns cálculos revelam que podemos escrever
Com isso, a parte da energia cinética de nossa equação só terá derivadas ao ![]() assumir que temos autoestados de
assumir que temos autoestados de ![]() .
.
A equação de Schrödinger, portanto, separa em uma parte angular (o ![]() termo) e uma parte radial (o resto). Com esta separação, esperamos (antecipando um pouco a solução angular)
termo) e uma parte radial (o resto). Com esta separação, esperamos (antecipando um pouco a solução angular)
será uma solução. O termo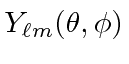 será de autofunções
será de autofunções ![]()
então a equação radial se torna
Devemos voltar a esta equação para cada 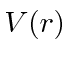 que desejamos resolver.
que desejamos resolver.
Nós resolver a parte angular do problema, em geral, usando operadores momento angular. Descobrimos que o momento angular é quantizado .
com ![]() e
e ![]() inteiros que satisfaçam a condição . Os operadores que aumentam e diminuem o componente do momento angular são
inteiros que satisfaçam a condição . Os operadores que aumentam e diminuem o componente do momento angular são 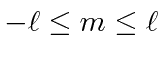
![]()
Derivamos a forma funcional dos Harmônicos esféricos usando a forma diferencial dos operadores de momento angular. 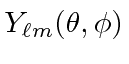
Soluções para a equação radial para potenciais constantes
Soluções para a equação radial em potencial constante são importantes, pois são as soluções para grandes ![]() potenciais de faixa limitada. Eles são, portanto, usados em problemas de dispersão como os estados de entrada e saída. As soluções são as funções esféricas de Bessel e as funções esféricas de Neumann.
potenciais de faixa limitada. Eles são, portanto, usados em problemas de dispersão como os estados de entrada e saída. As soluções são as funções esféricas de Bessel e as funções esféricas de Neumann.
onde 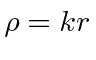 . A combinação linear dessas que cai adequadamente em geral
. A combinação linear dessas que cai adequadamente em geral ![]() é chamada de função de Hankel do primeiro tipo.
é chamada de função de Hankel do primeiro tipo.
Usamos essas soluções para fazer uma análise de onda parcial de espalhamento , resolver para estados vinculados de um poço de potencial esférico , resolver para estados vinculados de um poço esférico infinito (uma "caixa'' esférica) e resolver para espalhamento de um potencial esférico.
Hidrogênio
A equação radial do hidrogênio (potencial de Coulomb) é resolvida encontrando o comportamento de![]() em geral, em seguida, encontrando o comportamento de
em geral, em seguida, encontrando o comportamento de![]() pequeno , em seguida usando uma solução de séries de potências para obter
pequeno , em seguida usando uma solução de séries de potências para obter
com
Para manter a função de onda normalizável, a série de potências deve terminar, dando-nos nossa condição de autovalor de energia.
Aqui ![]() é chamado de número quântico principal e é dado por
é chamado de número quântico principal e é dado por
onde ![]() é o número de nós na função de onda radial. É uma característica estranha do hidrogênio que uma excitação radial e uma excitação angular tenham a mesma energia.
é o número de nós na função de onda radial. É uma característica estranha do hidrogênio que uma excitação radial e uma excitação angular tenham a mesma energia.
Portanto, um autoestado
de energia de hidrogênio é descrito por três números quânticos inteiros com requisitos de
e também um inteiro, e
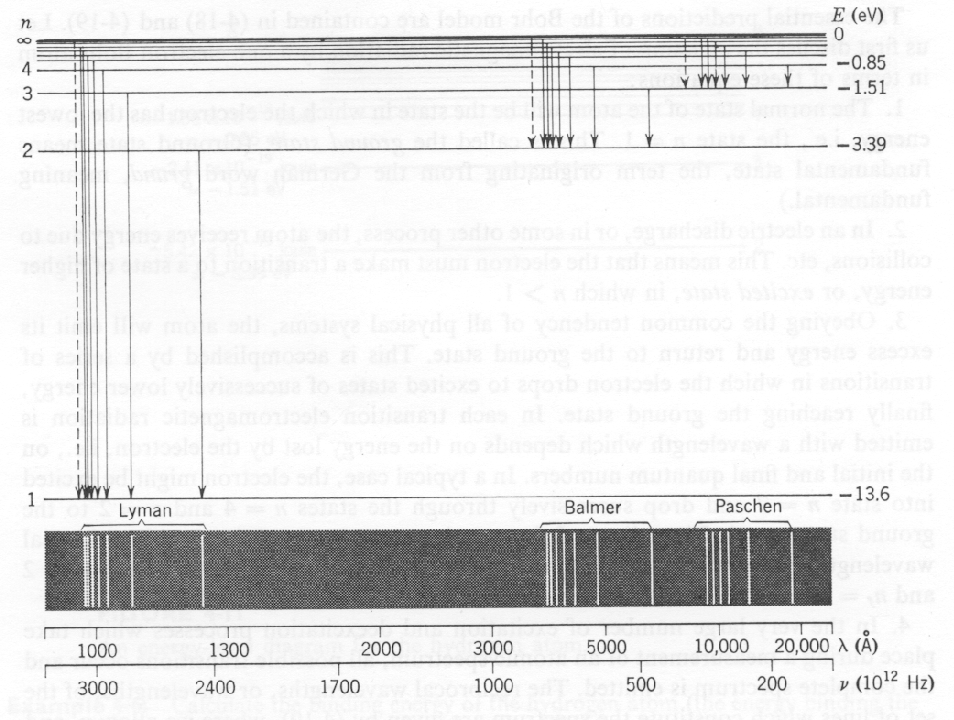
O estado fundamental do Hidrogênio é 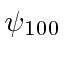 e tem energia de -13,6 eV. Calculamos vários dos autoestados de menor energia.
e tem energia de -13,6 eV. Calculamos vários dos autoestados de menor energia.
O diagrama abaixo mostra os estados de limite de energia mais baixos do hidrogênio e seus decaimentos típicos.
Solução do problema 3D do OH em coordenadas esféricas
Como exemplo de outro problema com simetria esférica, resolvemos o problema do oscilador harmônico simétrico 3D . Já resolvemos esse problema em coordenadas cartesianas. Agora usamos coordenadas esféricas e autofunções de momento angular.
As energias próprias são
onde ![]() é o número de nós na função de onda radial e
é o número de nós na função de onda radial e ![]() é o número quântico do momento angular total. Isso dá exatamente o mesmo conjunto de energias próprias que obtivemos na solução cartesiana, mas os estados próprios são agora estados de momento angular total definido e componente z do momento angular.
é o número quântico do momento angular total. Isso dá exatamente o mesmo conjunto de energias próprias que obtivemos na solução cartesiana, mas os estados próprios são agora estados de momento angular total definido e componente z do momento angular.
Representação Matricial de Operadores e Estados
Podemos definir os componentes de um vetor de estado ![]() como as projeções do estado em um conjunto ortonormal completo de estados, como as autofunções de um operador Hermitiano.
como as projeções do estado em um conjunto ortonormal completo de estados, como as autofunções de um operador Hermitiano.
Da mesma forma, podemos definir o elemento de matriz de um operador em termos de um par desses estados de base ortonormais
Com essas definições, problemas de Mecânica Quântica podem ser resolvidos usando os operadores e estados de representação de matrizes. Um operador agindo em um estado é uma matriz vezes um vetor.
O produto dos operadores é o produto das matrizes. Operadores que não comutam são representados por matrizes que não comutam.
Um estudo de operadores 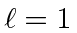 e autofunções
e autofunções
O conjunto de estados com o mesmo momento angular total e os operadores de momento angular que atuam sobre eles são frequentemente representados por vetores e matrizes. Por exemplo, os diferentes ![]() estados para
estados para ![]() serão representados por um vetor de 3 componentes e os operadores de momento angular representados por matrizes 3X3.
serão representados por um vetor de 3 componentes e os operadores de momento angular representados por matrizes 3X3.
Existem razões práticas e teóricas pelas quais esse conjunto de estados é separado dos estados com diferentes números quânticos de momento angular total.
Os estados são frequentemente (quase) degenerados e, portanto, devem ser tratados como um grupo por razões práticas.
Além disso, uma rotação dos eixos coordenados não mudará o número quântico total do momento angular, portanto, o operador de rotação trabalha dentro deste grupo de estados.
Escrevemos nossos 3 vetores de componentes da seguinte maneira.
As matrizes que representam os operadores de momento angular para ![]() são as seguintes
são as seguintes
As mesmas matrizes também representam o spin 1, ![]() mas é claro que atuariam em um espaço vetorial diferente.
mas é claro que atuariam em um espaço vetorial diferente.
Os operadores de rotação (operadores de simetria) são dados por
para a forma diferencial ou a forma matricial dos operadores.
Para![]() essas são matrizes 3X3 (unitárias). Nós as usamos quando precisamos redefinir a direção de nossos eixos coordenados. As rotações dos estados do momento angular não são iguais às rotações dos vetores no espaço 3. Os componentes dos vetores representam quantidades diferentes e, portanto, se transformam de maneira bastante diferente. Os "vetores'' que estamos usando para o momento angular na verdade deveriam ser chamados de espinores quando nos referimos às suas propriedades sob rotações e impulsos de Lorentz.
essas são matrizes 3X3 (unitárias). Nós as usamos quando precisamos redefinir a direção de nossos eixos coordenados. As rotações dos estados do momento angular não são iguais às rotações dos vetores no espaço 3. Os componentes dos vetores representam quantidades diferentes e, portanto, se transformam de maneira bastante diferente. Os "vetores'' que estamos usando para o momento angular na verdade deveriam ser chamados de espinores quando nos referimos às suas propriedades sob rotações e impulsos de Lorentz.
Spin 1/2 e outros 2 sistemas de estado
A álgebra do momento angular definida pelas relações de comutação entre os operadores requer que o número quântico do momento angular total seja um inteiro ou meio inteiro. A possibilidade de meio inteiro não era útil para o momento angular orbital porque não havia função harmônica esférica correspondente (valor único) para representar a amplitude para uma partícula estar em alguma posição.
A possibilidade de meio inteiro é usada para representar o momento angular interno de algumas partículas. O caso mais simples e importante é girar pela metade. Existem apenas dois estados possíveis com diferentes componentes z de spin: spin para cima 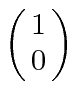 , com componente z do momento angular
, com componente z do momento angular 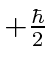 , e spin para baixo
, e spin para baixo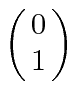 , com
, com 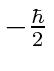 . Os operadores de rotação correspondentes são
. Os operadores de rotação correspondentes são
que satisfazem as relações de comutação usuais das quais derivamos as propriedades dos operadores de momento angular.
É comum definir as Matrizes de Pauli ![]() que possuem as seguintes propriedades.
que possuem as seguintes propriedades.
As duas últimas linhas afirmam que as matrizes de Pauli são anti-comutação. As matrizes ![]() são as matrizes Hermitianas e sem rastros de dimensão 2. Qualquer matriz 2 por 2 pode ser escrita como uma combinação linear das matrizes
são as matrizes Hermitianas e sem rastros de dimensão 2. Qualquer matriz 2 por 2 pode ser escrita como uma combinação linear das matrizes ![]() e da identidade.
e da identidade.
Mecânica Quântica em um Campo Eletromagnético
O hamiltoniano clássico para uma partícula em um campo eletromagnético é
onde ![]() é definido como um número positivo. Este hamiltoniano fornece a lei de força de Lorentz correta. Observe que o operador de momento agora incluirá o momento no campo, não apenas o momento da partícula. Como este hamiltoniano é escrito,
é definido como um número positivo. Este hamiltoniano fornece a lei de força de Lorentz correta. Observe que o operador de momento agora incluirá o momento no campo, não apenas o momento da partícula. Como este hamiltoniano é escrito, ![]() é a variável conjugada a
é a variável conjugada a ![]() e está relacionada à velocidade de
e está relacionada à velocidade de
Na Mecânica Quântica, o operador momentum é substituído da mesma maneira para incluir os efeitos dos campos magnéticos e, eventualmente, da radiação.
Partindo do hamiltoniano acima, derivamos o hamiltoniano para uma partícula em um campo magnético constante .
Isso tem o efeito familiar de um momento magnético paralelo ao vetor do momento angular, além de alguns termos adicionais que são muito pequenos para átomos em campos realizáveis em laboratório.
Então, para átomos, o termo adicional dominante é
onde
Este é, efetivamente, o momento magnético devido ao momento angular orbital do elétron.
Os outros termos podem ser importantes se um estado está espalhado por uma região muito maior do que um átomo.
Trabalhamos o exemplo de um plasma em um campo magnético constante. Uma partícula carregada no plasma tem o seguinte espectro de energia
que depende de 2 números quânticos.
![]() é o momento conservado ao longo da direção do campo que pode assumir qualquer valor.
é o momento conservado ao longo da direção do campo que pode assumir qualquer valor.
![]() é um número inteiro que lida com o estado em x e y.
é um número inteiro que lida com o estado em x e y.
Este problema pode ser simplificado usando-se alguns operadores de simetria diferentes. Nós o trabalhamos de duas maneiras diferentes: em uma se reduz à equação radial para o átomo de Hidrogênio; no outro, reduz-se à equação do oscilador harmônico, mostrando que esses dois problemas que podemos resolver são de alguma forma equivalentes.
Simetria de fase local em mecânica quântica e a simetria de calibre
Existe uma simetria na física que podemos chamar de Simetria de Fase Local na mecânica quântica. Nessa simetria, mudamos a fase da função de onda (do elétron) em uma quantidade diferente em todo o espaço-tempo. Para compensar essa mudança, precisamos também fazer uma transformação de calibre dos potenciais eletromagnéticos. Todos eles devem ir juntos assim.
A simetria de fase local requer que o eletromagnetismo exista e tenha uma simetria de calibre para que possamos manter a equação de Schrödinger invariante sob esta transformação de fase.
Exploramos a simetria do calibre em EM para mostrar que, em regiões livres de campo , a função ![]() pode ser simplesmente igual a uma integral de linha do potencial vetorial (se escolhermos o calibre correto).
pode ser simplesmente igual a uma integral de linha do potencial vetorial (se escolhermos o calibre correto).
Usamos isso para mostrar que o fluxo magnético encerrado por um supercondutor é quantizado.
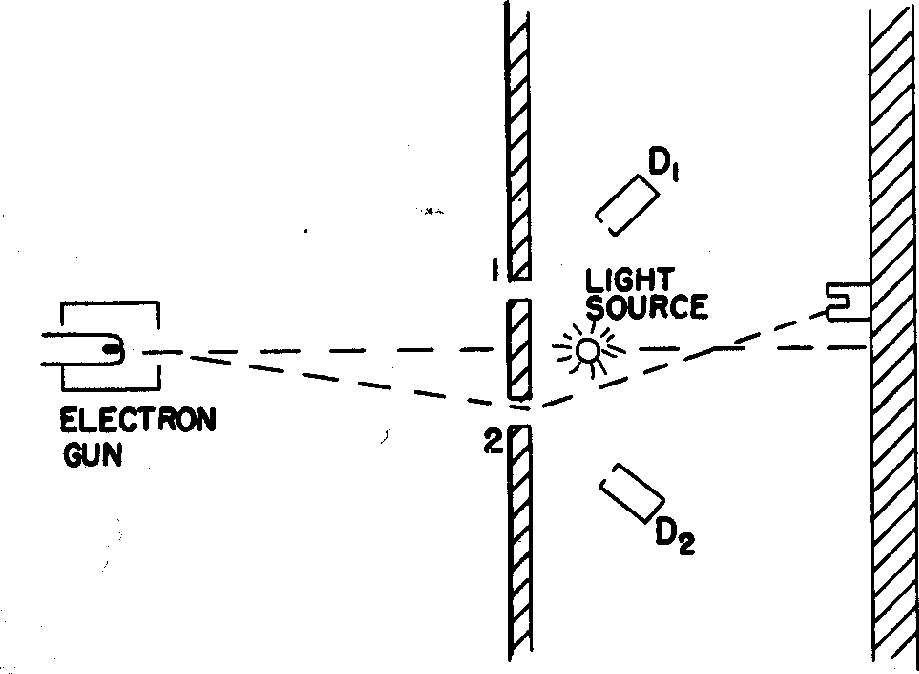
Também mostramos que os campos magnéticos podem ser usados para alterar os efeitos de interferência na mecânica quântica. O Efeito Aharanov Böhm nos traz de volta ao experimento de difração de duas fendas, mas adiciona campos magnéticos.
Os feixes de elétrons viajam por duas fendas em regiões livres de campo, mas temos a capacidade de variar um campo magnético delimitado pelo caminho dos elétrons. Na tela, as amplitudes das duas fendas interferem . Vamos começar com e em todos os lugares. Quando mudamos o campo, as funções de onda devem mudar. 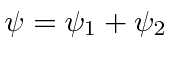
![]()
![]()
![]()
A fase relativa das duas fendas depende do fluxo entre as fendas. Variando o ![]() campo, mudaremos o padrão de difração , embora
campo, mudaremos o padrão de difração , embora ![]() ao longo de todo o caminho dos elétrons.
ao longo de todo o caminho dos elétrons.
Adição de Momentum Angular
Freqüentemente, é necessário adicionar o momento angular de duas (ou mais) fontes para obter estados de momento angular total definido. Por exemplo, na ausência de campos externos, os estados próprios de energia do Hidrogênio (incluindo todos os efeitos de estrutura fina) também são estados próprios do momento angular total . Isso quase tem que ser verdade se houver simetria esférica para o problema.
Como exemplo, vamos supor que estamos adicionando o momento angular orbital de dois elétrons ![]() e
e ![]() para obter um momento angular total
para obter um momento angular total ![]() . Mostraremos que o número quântico do momento angular total assume todos os valores na faixa
. Mostraremos que o número quântico do momento angular total assume todos os valores na faixa
Podemos entender isso qualitativamente no modelo vetorial ilustrado abaixo. Estamos adicionando dois vetores quânticos.
O comprimento do vetor resultante está em algum lugar entre a diferença de suas magnitudes e a soma de suas magnitudes, uma vez que não sabemos para qual direção os vetores estão apontando.
Os estados de momento angular total definido com números quânticos ![]() e
e ![]() , podem ser escritos em termos de produtos dos estados individuais (como o elétron 1 está neste estado E o elétron 2 está nesse estado). A expansão geral é chamada de série Clebsch-Gordan:
, podem ser escritos em termos de produtos dos estados individuais (como o elétron 1 está neste estado E o elétron 2 está nesse estado). A expansão geral é chamada de série Clebsch-Gordan:
ou em termos dos vetores ket
Os coeficientes de Clebsch-Gordan são tabulados, embora possamos calcular muitos deles nós mesmos.
Ao combinar estados de partículas idênticas, o estado de momento angular total mais alto,, 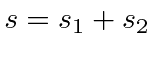 será sempre simétrico sob intercâmbio. A simetria sob o intercâmbio irá alternar conforme
será sempre simétrico sob intercâmbio. A simetria sob o intercâmbio irá alternar conforme ![]() é reduzida.
é reduzida.
O número total de estados é sempre preservado. Por exemplo, se eu adicionar dois ![]() estados, obtenho estados de momento angular total com
estados, obtenho estados de momento angular total com 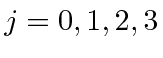 e 4. Existem 25 estados de produto, pois cada
e 4. Existem 25 estados de produto, pois cada ![]() estado tem 5 diferentes
estado tem 5 diferentes ![]() s possíveis . Compare isso com a soma do número de estados que acabamos de listar.
s possíveis . Compare isso com a soma do número de estados que acabamos de listar.
onde os números são o número de estados no multipleto.
Usaremos adição de momento angular para:
- Adicione o momento angular orbital ao momento angular de rotação de um elétron em um átomo ;
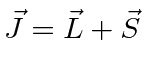
- Some os momentos angulares orbitais de dois elétrons em um átomo ;
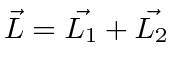
- Some os spins de duas partículas ;
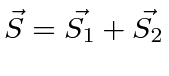
- Adicione o spin nuclear ao momento angular atômico total ;
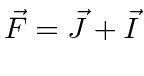
- Some os momentos angulares totais de dois elétrons ;
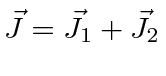
- Some o momento angular orbital total ao momento angular de spin total para uma coleção de elétrons em um átomo ;
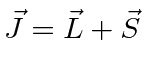
- Escreva o produto dos harmônicos esféricos em termos de uma soma de harmônicos esféricos.
Teoria da Perturbação Independente do Tempo
Suponha que já resolvemos um problema de autovalor de energia e agora precisamos incluir um termo adicional no hamiltoniano. Podemos usar a teoria de perturbação independente do tempo para calcular correções para os autovalores e estados próprios da energia. Se a equação de Schrödinger para o problema completo for
e já resolvemos o problema dos autovalores ![]() , pois podemos usar uma série de perturbações, para expandir nossos autovalores de energia e autossados em potências da pequena perturbação.
, pois podemos usar uma série de perturbações, para expandir nossos autovalores de energia e autossados em potências da pequena perturbação.
onde o sobrescrito (0), (1), (2) são os termos zero, de primeira e de segunda ordem na série. ![]() existe para manter a função de onda normalizada, mas não terá um papel importante em nossos resultados.
existe para manter a função de onda normalizada, mas não terá um papel importante em nossos resultados.
Resolvendo a equação de Schrödinger em cada ordem da série de perturbações, calculamos as correções para as energias e autofunções. Fornecemos apenas os primeiros termos acima.
Um problema surge no caso de estados degenerados ou quase degenerados. O denominador de energia na última equação acima é pequeno e a série não converge. Para lidar com este caso, precisamos rediagonalizar o hamiltoniano completo no subespaço de estados quase degenerados.
Este é apenas o problema de autovalor padrão para o hamiltoniano completo no subespaço de estados (quase) degenerados.
Usaremos a teoria de perturbação independente do tempo para calcular estruturas finas e correções hiperfinas para energias de hidrogênio, bem como para muitos outros cálculos. A teoria de perturbação de estado degenerado será usada para o Efeito Stark e para a divisão hiperfina em Hidrogênio.
A Estrutura Fina do Hidrogênio
Resolvemos o problema de um elétron não relativístico e sem spin em um potencial coulomb exatamente. Os átomos de hidrogênio reais têm várias pequenas correções para essa solução simples. Se dissermos que o spin do elétron é um efeito relativístico, todas elas podem ser chamadas de correções relativísticas, que estão fora de ordem em ![]() comparação com as energias de hidrogênio que calculamos.
comparação com as energias de hidrogênio que calculamos.
- A correção relativística da energia cinética do elétron.
- A correção Spin-Orbit.
- A correção do `` Termo de Darwin '' para os estados da equação de Dirac.
Calculando esses efeitos de estrutura fina separadamente e somando-os, descobrimos que obtemos um bom cancelamento que resulta em uma fórmula simples.
A correção depende apenas do número quântico angular total e não depende ![]() dos estados de diferentes momentos angulares totais divididos em energia, mas ainda há uma boa dose de degenerescência. Faz sentido, para um problema com simetria esférica, que os estados de momento angular total definido sejam os autoestados de energia e dos quais o resultado dependa
dos estados de diferentes momentos angulares totais divididos em energia, mas ainda há uma boa dose de degenerescência. Faz sentido, para um problema com simetria esférica, que os estados de momento angular total definido sejam os autoestados de energia e dos quais o resultado dependa ![]() .
.
Também calculamos o efeito Zeeman no qual um campo magnético externo é aplicado ao hidrogênio. O campo externo é muito importante, pois quebra a simetria esférica e divide os estados degenerados, permitindo entender o Hidrogênio por meio da espectroscopia.
A correção devido a um campo magnético fraco é encontrada para ser
O fator é conhecido como Fator Lande porque o estado se divide como se tivesse essa razão giromagnética. Sabemos que é de fato uma combinação dos fatores orbitais e de spin g em um estado de definido . Assumimos que o efeito do campo é pequeno em comparação com as correções de estrutura fina. Podemos escrever a energia total em um campo magnético fraco. 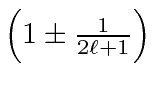
![]()
![]()
Assim, em um campo fraco, a degeneração é completamente quebrada para os estados 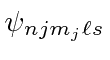 . Todos os estados podem ser detectados espectroscopicamente.
. Todos os estados podem ser detectados espectroscopicamente.
No limite forte campo poderíamos usar estados de definitiva ![]() e
e ![]() e calcular os efeitos da estrutura fina,
e calcular os efeitos da estrutura fina, 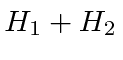 como uma perturbação. Em um campo de força intermediária, da ordem de 500 Gauss, a combinação da Hamiltoniana da estrutura fina do Hidrogênio e o termo para o campo B deve ser diagonalizado no conjunto de estados com o mesmo número quântico principal
como uma perturbação. Em um campo de força intermediária, da ordem de 500 Gauss, a combinação da Hamiltoniana da estrutura fina do Hidrogênio e o termo para o campo B deve ser diagonalizado no conjunto de estados com o mesmo número quântico principal ![]() .
.
Estrutura Hiperfina
A interação entre o spin do núcleo e o momento angular do elétron causa uma divisão adicional (hiperfina) dos estados atômicos. É chamado de hiperfino porque também é ordenado ![]() como as correções de estrutura fina, mas é menor por um fator de aproximadamente por causa da dependência de massa do momento magnético de rotação para as partículas.
como as correções de estrutura fina, mas é menor por um fator de aproximadamente por causa da dependência de massa do momento magnético de rotação para as partículas. 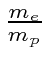
O momento magnético do núcleo é
onde ![]() está o vetor de spin nuclear . Como o núcleo, o próton e o nêutron têm estrutura interna, a razão giromagnética nuclear não é apenas 2. Para o próton, é .
está o vetor de spin nuclear . Como o núcleo, o próton e o nêutron têm estrutura interna, a razão giromagnética nuclear não é apenas 2. Para o próton, é . 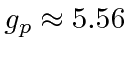
Calculamos a contribuição hiperfina para o hamiltoniano para ![]() estados.
estados.
Agora, assim como no caso da interação spin-órbita, vamos definir o momento angular total ![]()
Está nos estados de definido ![]() e
e 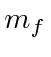 que a perturbação hiperfina será diagonal. Em essência, estamos fazendo a teoria da perturbação de estado degenerada. Poderíamos diagonalizar a matriz 4 por 4 para a perturbação para resolver o problema ou podemos usar o que sabemos para escolher os estados corretos para começar. Novamente, como a interação da órbita do spin, os estados de momento angular total serão os estados corretos porque podemos escrever a perturbação em termos de números quânticos desses estados.
que a perturbação hiperfina será diagonal. Em essência, estamos fazendo a teoria da perturbação de estado degenerada. Poderíamos diagonalizar a matriz 4 por 4 para a perturbação para resolver o problema ou podemos usar o que sabemos para escolher os estados corretos para começar. Novamente, como a interação da órbita do spin, os estados de momento angular total serão os estados corretos porque podemos escrever a perturbação em termos de números quânticos desses estados.
Para o estado fundamental do hidrogênio, estamos apenas adicionando duas ![]() partículas de spin , então os valores possíveis são
partículas de spin , então os valores possíveis são 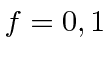 . A transição entre os dois estados dá origem a ondas EM com
. A transição entre os dois estados dá origem a ondas EM com ![]() cm.
cm.
Vamos trabalhar o efeito de um campo B externo nos estados hiperfinos do Hidrogênio, tanto no campo forte quanto na aproximação do campo fraco. Também resolvemos o problema sem uma aproximação de intensidade de campo. O resultado da intensidade do campo intermediário sempre aplicável é que os quatro estados têm energias que dependem da intensidade do campo B. Dois dos estados próprios de energia se misturam de uma forma que também depende de B. As quatro energias são
O átomo de hélio
O hamiltoniano para o hélio tem os mesmos termos do hidrogênio, mas tem uma grande perturbação devido à repulsão entre os dois elétrons.
Observe que a perturbação devido à repulsão entre os dois elétrons é aproximadamente do mesmo tamanho que o resto do hamiltoniano, então a teoria de perturbação de primeira ordem é improvável que seja precisa.
O estado fundamental do Hélio tem dois elétrons no nível 1s . Como o estado espacial é simétrico, a parte do spin do estado deve ser anti-simétrica ![]() (como sempre é para cascas fechadas). Para nossos autoestados de energia de ordem zero, usaremos estados de produto de funções de onda de hidrogênio
(como sempre é para cascas fechadas). Para nossos autoestados de energia de ordem zero, usaremos estados de produto de funções de onda de hidrogênio
e ignorar a perturbação. A energia para dois elétrons no estado (1s) para ![]() é então eV.
é então eV. ![]()
Podemos estimar a energia do estado fundamental na teoria de perturbação de primeira ordem , usando o termo de repulsão de elétrons como uma perturbação (muito grande). Isso não é muito preciso.
Podemos melhorar a estimativa da energia do estado fundamental usando o princípio variacional . O principal problema com nossa estimativa da teoria de perturbação é que não estamos contabilizando as mudanças na função de onda dos elétrons devido à triagem . Podemos fazer isso em alguma aproximação razoável, reduzindo a carga do núcleo na função de onda (não no hamiltoniano). Com o parâmetro ![]() , obtemos uma melhor estimativa da energia.
, obtemos uma melhor estimativa da energia.
| Cálculo | Energia | 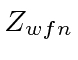 |
| -108,8 | 2 | |
| -74,8 | 2 | |
| -77,38 | ||
| Real | -78.975 |
Observe que o cálculo variacional ainda usa a teoria de perturbação de primeira ordem. Ele apenas adiciona um parâmetro variável à função de onda que usamos para minimizar a energia. Isso só funciona para o estado fundamental e para outros estados especiais.
Existe apenas um 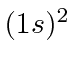 estado permitido e é o estado fundamental. Para estados excitados , os estados espaciais são (geralmente) diferentes, então eles podem ser simétricos ou anti-simétricos (sob o intercâmbio dos dois elétrons). Acontece que o estado anti-simétrico mantém os elétrons mais separados, então a repulsão é menor e a energia é menor. Se o estado espacial for antissimétrico, então o estado de spin é simétrico, s = 1. Portanto, os estados tripletos são geralmente significativamente mais baixos em energia do que os estados singuletos de spin correspondentes. Esta parece ser uma forte interação dependente do spin, mas na verdade é apenas o efeito da repulsão entre os elétrons, tendo um grande efeito dependendo da simetria do estado espacial e, portanto, da simetria do estado de spin.
estado permitido e é o estado fundamental. Para estados excitados , os estados espaciais são (geralmente) diferentes, então eles podem ser simétricos ou anti-simétricos (sob o intercâmbio dos dois elétrons). Acontece que o estado anti-simétrico mantém os elétrons mais separados, então a repulsão é menor e a energia é menor. Se o estado espacial for antissimétrico, então o estado de spin é simétrico, s = 1. Portanto, os estados tripletos são geralmente significativamente mais baixos em energia do que os estados singuletos de spin correspondentes. Esta parece ser uma forte interação dependente do spin, mas na verdade é apenas o efeito da repulsão entre os elétrons, tendo um grande efeito dependendo da simetria do estado espacial e, portanto, da simetria do estado de spin.
O primeiro estado de saída tem o conteúdo do estado hidrogenico de (1s) (2s) e tem s = 1. Calculamos a energia deste estado.
Aprenderemos mais tarde que as transições eletromagnéticas que mudam o spin são fortemente suprimidas, fazendo com que o tripleto de spin (ortohelium) e os estados de spin singlet (parahelium) tenham cadeias de decaimento quase separadas.
Física Atômica
O hamiltoniano para um átomo com elétrons e prótons Z tem muitos termos que representam a repulsão entre cada par de elétrons.
Vimos que a repulsão coulombiana entre elétrons é uma correção muito grande no Hélio e que o problema dos três corpos na mecânica quântica só é resolvido por aproximação.
A física das conchas fechadas e do momento angular nos permite entender até mesmo os átomos mais complexos. Quando temos elétrons suficientes para preencher uma camada, digamos 1s ou 2p, a distribuição de elétrons resultante é esfericamente simétrica porque
Com todos os estados preenchidos e as fases relativas determinadas pela antissimetria exigida por Pauli, os números quânticos da casca fechada são determinados. Existe apenas um estado possível que representa uma casca fechada e os números quânticos são
A cápsula fechada protege a carga nuclear. Por causa da triagem , o potencial não tem mais um ![]() comportamento puro . Os elétrons que estão distantes do núcleo percebem menos a carga nuclear e aumentam sua energia. Vemos que as camadas atômicas são preenchidas na ordem 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p. O efeito da triagem aumentando a energia dos
comportamento puro . Os elétrons que estão distantes do núcleo percebem menos a carga nuclear e aumentam sua energia. Vemos que as camadas atômicas são preenchidas na ordem 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p. O efeito da triagem aumentando a energia dos ![]() estados superiores é claro. Não é de admirar que a tabela periódica não seja totalmente periódica.
estados superiores é claro. Não é de admirar que a tabela periódica não seja totalmente periódica.
Um conjunto de diretrizes, conhecido como regras de Hund, nos ajuda a determinar os números quânticos para os estados fundamentais dos átomos. As conchas hidrogenadas se enchem dando 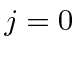 estados bem definidos para as conchas fechadas. À medida que adicionamos elétrons de valência , seguimos as regras de Hund para determinar o estado fundamental. Conseguimos uma grande simplificação tratando cascas quase fechadas como cascas fechadas mais buracos de rotação com carga positiva . Por exemplo, se um átomo tem dois elétrons aquém de uma camada fechada, nós o tratamos como uma camada fechada mais dois buracos positivos.)
estados bem definidos para as conchas fechadas. À medida que adicionamos elétrons de valência , seguimos as regras de Hund para determinar o estado fundamental. Conseguimos uma grande simplificação tratando cascas quase fechadas como cascas fechadas mais buracos de rotação com carga positiva . Por exemplo, se um átomo tem dois elétrons aquém de uma camada fechada, nós o tratamos como uma camada fechada mais dois buracos positivos.) ![]()
- Acople os elétrons de valência (ou lacunas) para dar o spin total máximo .
- Agora escolha o estado de máximo
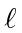 (sujeito ao princípio de Pauli. O princípio de Pauli em vez da regra, muitas vezes determina tudo aqui).
(sujeito ao princípio de Pauli. O princípio de Pauli em vez da regra, muitas vezes determina tudo aqui). - Se a casca estiver mais da metade cheia, escolha o estado de momento angular total mais alto,
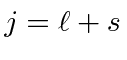 caso contrário, escolha o mais baixo
caso contrário, escolha o mais baixo 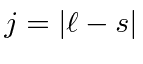 .
.
Moléculas
Podemos estudar moléculas simples para entender os fenômenos físicos das moléculas em geral. A molécula mais simples com a qual podemos trabalhar é o íon 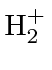 . Possui dois núcleos (A e B) compartilhando um elétron (1).
. Possui dois núcleos (A e B) compartilhando um elétron (1).
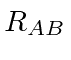 é a distância entre os dois núcleos. Calculamos a energia do estado fundamental usando os estados do hidrogênio como base.
é a distância entre os dois núcleos. Calculamos a energia do estado fundamental usando os estados do hidrogênio como base.
A função de onda de energia mais baixa pode ser considerada uma combinação linear (anti) simétrica de um elétron no estado fundamental próximo ao núcleo A e o estado fundamental próximo ao núcleo B
onde é gs ao redor do núcleo A. e não são ortogonais; há sobreposição. O estado simétrico (ligação) tem uma grande probabilidade de o elétron ser encontrado entre os núcleos . O estado antissimétrico (anticoagulante) tem uma pequena probabilidade e, portanto, uma energia muito maior. Lembre-se de que essa simetria é a da função de onda de um elétron ao redor dos dois núcleos. 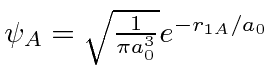
![]()
A ![]() molécula também é simples e sua energia pode ser calculada com a ajuda do cálculo anterior. O estado simétrico do espaço será o estado fundamental.
molécula também é simples e sua energia pode ser calculada com a ajuda do cálculo anterior. O estado simétrico do espaço será o estado fundamental.
A molécula pode vibrar no potencial criado quando o elétron compartilhado une os átomos, dando origem a um espectro de energia do oscilador harmônico.
As moléculas podem girar como corpos rígidos clássicos sujeitos à restrição de que o momento angular é quantizado em unidades de ![]() .
.
Teoria da Perturbação Dependente do Tempo
Usamos a teoria de perturbação independente do tempo para encontrar as mudanças de energia dos estados e para encontrar a mudança nos autoestados de energia na presença de uma pequena perturbação. Agora consideramos o caso de uma perturbação ![]() que é dependente do tempo . Tal perturbação pode causar transições entre estados próprios de energia . Vamos calcular a taxa dessas transições.
que é dependente do tempo . Tal perturbação pode causar transições entre estados próprios de energia . Vamos calcular a taxa dessas transições.
Derivamos uma equação para a taxa de variação da amplitude no estado próprio de ![]() energia .
energia .
Supondo que no ![]() sistema quântico comece em algum estado inicial
sistema quântico comece em algum estado inicial![]() , derivamos a amplitude para estar em um estado final
, derivamos a amplitude para estar em um estado final![]() .
.
Um caso importante de potencial dependente do tempo é uma perturbação oscilante senoidal pura (harmônica) . Podemos compensar qualquer dependência de tempo a partir de uma combinação linear de ondas seno e cosseno. Com alguns cálculos, derivamos a taxa de transição em um potencial harmônico de frequência ![]() .
.
Ele contém uma função delta de conservação de energia. A função delta pode parecer estranha. A taxa de transição seria zero se a energia não fosse conservada e infinita se a energia fosse exatamente conservada. Podemos entender isso se houver uma função de distribuição do  potencial de perturbação ou se houver um contínuo de estados finais que precisamos integrar. Em qualquer caso, a função delta nos ajuda a fazer a integral de maneira simples.
potencial de perturbação ou se houver um contínuo de estados finais que precisamos integrar. Em qualquer caso, a função delta nos ajuda a fazer a integral de maneira simples.
Radiação em átomos
A interação de átomos com ondas eletromagnéticas pode ser calculada usando a teoria de perturbação dependente do tempo. O problema atômico é resolvido na ausência de ondas EM, então os termos do vetor potencial no hamiltoniano podem ser tratados como uma perturbação.
Em um medidor em que , a perturbação é ![]()
Para a maioria dos decaimentos atômicos, o ![]() termo pode ser desprezado, pois é muito menor do que o termo. Tanto a decadência dos estados atômicos excitados com a emissão da radiação quanto a excitação dos átomos com a absorção da radiação podem ser calculadas.
termo pode ser desprezado, pois é muito menor do que o termo. Tanto a decadência dos estados atômicos excitados com a emissão da radiação quanto a excitação dos átomos com a absorção da radiação podem ser calculadas. 
Um campo EM arbitrário pode ser analisado por Fourier para fornecer uma soma de componentes de frequência definida. Considere o potencial vetorial para um desses componentes ,. A energia no campo é . Se o campo for quantizado (como mostraremos mais tarde) com fótons de energia , podemos escrever a intensidade do campo em termos do número de fótons .
A direção do campo é dada pelo vetor de polarização unitária . O termo cosseno foi dividido em exponenciais positivas e negativas. Na teoria das perturbações dependentes do tempo, o exponencial positivo corresponde à absorção de um fóton e excitação do átomo e o exponencial negativo corresponde à emissão de um fóton e decaimento do átomo para um estado de energia inferior. ![]()
Pense no campo EM como um oscilador harmônico em cada frequência, o exponencial negativo corresponde a um operador de aumento para o campo e o exponencial positivo a um operador de redução. Em analogia ao oscilador harmônico 1D quântico, substituímos 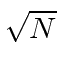 por
por 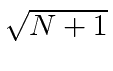 no caso do operador ascendente.
no caso do operador ascendente.
Com esta mudança, que posteriormente será justificada com a quantização do campo, ocorre uma perturbação mesmo sem campo aplicado ( ![]() )
)
que pode causar decaimento de estados atômicos.
Conectando este ![]() campo nas equações de perturbação dependentes do tempo de primeira ordem, a taxa de decaimento para um estado atômico pode ser calculada.
campo nas equações de perturbação dependentes do tempo de primeira ordem, a taxa de decaimento para um estado atômico pode ser calculada.
O quadrado absoluto da integral de tempo da teoria de perturbação produz a função delta de conservação de energia.
Para obter a taxa de decaimento total, devemos somar os estados finais permitidos. Podemos supor que o átomo permanece em repouso como uma boa aproximação, mas os estados finais do fóton devem ser cuidadosamente considerados. Aplicando condições de contorno periódicas em um volume cúbico ![]() , a integral sobre os estados finais pode ser feita conforme indicado abaixo.
, a integral sobre os estados finais pode ser feita conforme indicado abaixo.
Com esta integral de espaço de fase feita com a ajuda da função delta, a fórmula geral para a taxa de decaimento é
Essa taxa de decaimento ainda contém a integral sobre as direções dos fótons e uma soma sobre a polarização do estado final.
O cálculo do elemento da matriz atômica é geralmente feito na aproximação do dipolo elétrico
o que é válido se o comprimento de onda do fóton for muito maior que o tamanho do átomo. Com a ajuda de algumas relações de comutação, a fórmula da taxa de decaimento torna-se
O elemento da matriz atômica do operador vetorial ![]() é zero, a menos que certas restrições no momento angular dos estados inicial e final sejam satisfeitas. As regras de seleção para transições de dipolo elétrico (E1) são:
é zero, a menos que certas restrições no momento angular dos estados inicial e final sejam satisfeitas. As regras de seleção para transições de dipolo elétrico (E1) são:
Este é o resultado do teorema de Wigner-Eckart que afirma que o elemento da matriz de um operador vetorial ![]() , onde o inteiro
, onde o inteiro ![]() vai de -1 a +1, é dado por
vai de -1 a +1, é dado por
Aqui ![]() representa todos os (outros) números quânticos do estado, não os números quânticos do momento angular. No caso de um operador espacial simples como
representa todos os (outros) números quânticos do estado, não os números quânticos do momento angular. No caso de um operador espacial simples como ![]() , apenas o momento angular orbital está envolvido.
, apenas o momento angular orbital está envolvido.
Derivamos um resultado simples para a taxa de decaimento total de um estado, somada sobre a polarização final do fóton e integrada sobre a direção do fóton
Isso pode ser usado para calcular facilmente as taxas de decaimento do hidrogênio, por exemplo, a taxa de decaimento 2p.
A taxa de decaimento total está relacionada à largura de energia de um estado excitado, como pode ser esperado do princípio da incerteza. A largura total na metade do máximo (FWHM) da distribuição de energia de um estado é . A distribuição de frequência segue uma distribuição Breit-Wigner. 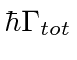
Além da largura de energia inerente de um estado, outros efeitos podem influenciar as larguras medidas, incluindo alargamento de colisão, alargamento Doppler e recuo atômico.
A teoria quântica da radiação EM pode ser usada para entender muitos fenômenos, incluindo distribuições angulares de fótons, polarização de fótons, LASERs, o efeito Mössbauer, o efeito fotoelétrico, o espalhamento de luz e a absorção de raios-x.
Teoria de Campo Clássica
Uma revisão da teoria de campo clássica é útil para fundamentar nosso desenvolvimento de teorias quânticas relativísticas de campo para fótons e elétrons. Vamos trabalhar com 4 vetores como o vetor de coordenadas abaixo
usando o ![]() para obter a
para obter a ![]() no termo de tempo em um produto escalar (em vez de usar um tensor métrico).
no termo de tempo em um produto escalar (em vez de usar um tensor métrico).
Uma densidade Lagrangiana escalar de Lorentz será derivada para cada teoria de campo que construirmos. Do Lagrangiano podemos derivar uma equação de campo chamada equação de Euler-Lagrange.
O Lagrangiano para um campo escalar massivo ![]() pode ser deduzido do requisito de que seja um campo escalar
pode ser deduzido do requisito de que seja um campo escalar
onde o último termo é a interação com uma fonte. A equação de Euler-Lagrange dá
que é conhecida como a equação de Klein-Gordon com uma fonte e é uma equação relativística razoável para um campo escalar.
Usando as transformadas de Fourier, o campo de uma fonte pontual pode ser calculado
Este é um campo que cai muito mais rápido do que ![]() . Um campo escalar massivo cai exponencialmente e quanto maior a massa, mais rápida é a queda. Isso se encaixa muito bem na forma da força entre os núcleons, embora a força nuclear real precise de um estudo muito mais detalhado.
. Um campo escalar massivo cai exponencialmente e quanto maior a massa, mais rápida é a queda. Isso se encaixa muito bem na forma da força entre os núcleons, embora a força nuclear real precise de um estudo muito mais detalhado.
O Campo Eletromagnético Clássico
Para o estudo do campo de Maxwell, é mais conveniente fazer uma pequena modificação no sistema de unidades usado. Nas unidades Racionalizadas de Heaviside-Lorentz, os campos são todos reduzidos por um fator de 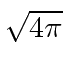 e as cargas são aumentadas pelo mesmo fator. Com essa mudança, as equações de Maxwell, assim como as Lagrangianas que usamos, são simplificadas. Teria simplificado muitas coisas se Maxwell tivesse começado com este conjunto de unidades.
e as cargas são aumentadas pelo mesmo fator. Com essa mudança, as equações de Maxwell, assim como as Lagrangianas que usamos, são simplificadas. Teria simplificado muitas coisas se Maxwell tivesse começado com este conjunto de unidades.
Como é bem conhecido pela eletricidade e magnetismo clássicos, os componentes do campo elétrico e magnético são, na verdade, elementos de um tensor de Lorentz de categoria 2.
Este tensor de campo pode simplesmente ser escrito em termos do potencial vetorial , (que é um vetor de Lorentz).
Observe que 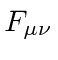 é automaticamente anti-simétrico sob o intercâmbio dos índices.
é automaticamente anti-simétrico sob o intercâmbio dos índices.
Com os campos derivados do potencial vetorial, duas das equações de Maxwell são satisfeitas automaticamente. As duas equações restantes podem ser escritas como uma equação de 4 vetores.
Agora queremos escolher um Lagrangiano escalar. Visto que E&M é uma teoria bem compreendida, o Lagrangiano que é conhecido por fornecer as equações corretas também é conhecido.
Observe que (além da velocidade da luz não ser definida como 1), o Lagrangiano não contém constantes desnecessárias neste conjunto de unidades. O último termo é um termo fonte que fornece a interação entre o campo EM e partículas carregadas. Ao trabalhar com este Lagrangiano, trataremos cada componente de ![]() como um campo independente. Neste caso, a equação de Euler-Lagrange é a equação de Maxwell conforme escrita acima.
como um campo independente. Neste caso, a equação de Euler-Lagrange é a equação de Maxwell conforme escrita acima.
A densidade hamiltoniana de campo livre pode ser calculada de acordo com a prescrição padrão que produz
se não houver termos de origem na região.
A simetria de calibre pode ser usada para colocar uma condição no potencial do vetor.
Isso é chamado de condição de Lorentz . Mesmo com isso satisfeito, ainda há uma liberdade de medida substancial possível. As transformações de calibre podem ser feitas conforme mostrado abaixo.
Quantização do campo EM
O hamiltoniano para o campo de Maxwell pode ser usado para quantizar o campo da mesma forma que a mecânica de uma onda dimensional foi quantizada. O campo de radiação pode ser mostrado como a parte transversal do campo, 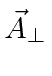 enquanto as cargas estáticas dão origem a
enquanto as cargas estáticas dão origem a ![]() e
e ![]() .
.
Nós decompor o campo de radiação em seus componentes de Fourier
onde são vetores unitários reais, e é o coeficiente da onda com o vetor de onda e o vetor de polarização . Uma vez que o vector de onda é escolhido, os dois vectores de polarização deve ser escolhido de modo que , e formar um sistema ortogonal destro . ![]()
![]()
![]()
![]()
![]()
![]()
Conectando a decomposição de Fourier na fórmula para a densidade hamiltoniana e usando a natureza transversal do campo de radiação, podemos calcular o hamiltoniano (densidade integrada sobre o volume).
Este hamiltoniano será usado para quantizar o campo EM. Ao calcular o hamiltoniano, foi tomado cuidado para não comutar os coeficientes de Fourier e seus conjugados.
A coordenada canônica e os momentos podem ser encontrados
para o oscilador harmônico em cada frequência. Assumimos que uma coordenada e seu momento conjugado têm o mesmo comutador que na mecânica das ondas e que as coordenadas de diferentes osciladores comutam.
Como foi feito para o oscilador harmônico 1D, escrevemos o hamiltoniano em termos de operadores de aumento e redução que têm as mesmas relações de comutação do oscilador harmônico 1D.
Isso significa que tudo o que sabemos sobre os operadores de subida e descida se aplica aqui. As energias estão em etapas ![]() e deve haver um estado fundamental. Os estados podem ser rotulados por um número quântico
e deve haver um estado fundamental. Os estados podem ser rotulados por um número quântico  .
.
Os coeficientes de Fourier agora podem ser escritos em termos dos operadores de aumento e redução para o campo.
Os estados do campo são dados pelo número de ocupação de cada estado possível de fóton.
Qualquer estado pode ser construído operando com operadores de criação no estado de vácuo. Qualquer estado com vários fótons será automaticamente simétrico sob o intercâmbio de pares de fótons porque os operadores comutam.
Este é essencialmente o mesmo resultado que nossa estimativa anterior de colocar um 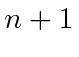 no operador de emissão.
no operador de emissão.
Agora podemos escrever o campo de radiação quantizado em termos dos operadores em ![]() .
.
Além da aproximação do dipolo elétrico, o próximo termo na expansão é . Este termo é dividido de acordo com suas propriedades de rotação e transformação de Lorentz em termos de Quadrupolo Elétrico e Dipolo Magnético. A interação do spin do elétron com o campo magnético é da mesma ordem e deve ser incluída junto com os termos E2 e M1. ![]()
![]()
O termo Quadrupolo Elétrico (E2) não muda a paridade e nos dá a regra de seleção.
O termo dipolo magnético (M1) não altera a paridade, mas pode alterar o spin. Como é um operador vetorial (axial), ele muda o momento angular em 0, +1 ou -1 unidade.
O campo quantizado é muito útil na derivação da fórmula de radiação do corpo negro de Plank que deu início à revolução quântica. Ao equilibrar as taxas de reação proporcionais ![]() e
e 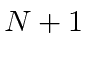 para absorção e emissão em equilíbrio, a densidade de energia no campo de radiação dentro de uma cavidade é facilmente derivada.
para absorção e emissão em equilíbrio, a densidade de energia no campo de radiação dentro de uma cavidade é facilmente derivada.
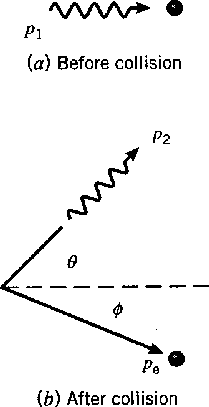
Dispersão de fótons
34 O campo de fótons quantizado pode ser usado para calcular a seção transversal para espalhamento de fótons. A aproximação de dipolo elétrico é usada para simplificar o elemento da matriz atômica em baixa energia, onde o comprimento de onda é longo em comparação com o tamanho atômico.
Para espalhar um fóton, o campo deve agir duas vezes, uma para aniquilar o fóton de estado inicial e outra para criar o fóton de estado final. Uma vez que o campo quantizado contém operadores de criação e aniquilação,
tanto o ![]() termo de primeira ordem quanto o termo de segunda ordem podem contribuir para a dispersão. Ambas as amplitudes são adequadas .
termo de primeira ordem quanto o termo de segunda ordem podem contribuir para a dispersão. Ambas as amplitudes são adequadas . 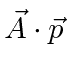
![]()
O elemento de matriz do ![]() termo para ir de um fóton de vetor de onda
termo para ir de um fóton de vetor de onda ![]() e um estado atômico
e um estado atômico ![]() a um fóton espalhado de vetor de onda
a um fóton espalhado de vetor de onda ![]() e um estado atômico
e um estado atômico ![]() é particularmente simples, pois não contém coordenadas atômicas ou momentos.
é particularmente simples, pois não contém coordenadas atômicas ou momentos.
Os termos de segunda ordem podem mudar os estados atômicos por causa do ![]() operador.
operador.
A seção transversal para espalhamento de fótons é então dada pelo
Fórmula de Kramers-Heisenberg . Os três termos vêm dos três diagramas de Feynman que contribuem para o espalhamento na ordem ![]() .
.
Este resultado pode ser especializado para o caso de espalhamento elástico, com o auxílio de alguns comutadores.
Lord Rayleigh calculou o espalhamento elástico de baixa energia da luz dos átomos usando o eletromagnetismo clássico. Se a energia do fóton espalhado é menor do que a energia necessária para excitar o átomo, então a seção transversal é proporcional a ![]() , de modo que a luz azul se espalha mais do que a luz vermelha nos gases incolores em nossa atmosfera.
, de modo que a luz azul se espalha mais do que a luz vermelha nos gases incolores em nossa atmosfera.
Se a energia do fóton espalhado for muito maior do que a energia de ligação do átomo, 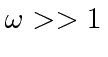 eV. então a seção transversal se aproxima daquela do espalhamento de um elétron livre, Thomson Scattering .
eV. então a seção transversal se aproxima daquela do espalhamento de um elétron livre, Thomson Scattering .
O espalhamento é aproximadamente independente de energia e a única dependência angular é da polarização. A luz dispersa pode ser polarizada mesmo que a luz incidente não o seja.
Electron Self Energy
Mesmo no eletromagnetismo clássico, se alguém puder calcular a energia necessária para montar um elétron, o resultado é infinito, mas os elétrons existem. A correção da autoenergia quântica também é infinita, embora possa ser considerada finita se aceitarmos o fato de que nossas teorias não são válidas até energias infinitas.
A correção da autoenergia quântica tem efeitos importantes e mensuráveis. Ele causa mudanças observáveis de energia no Hidrogênio e nos ajuda a resolver o problema dos infinitos devido aos denominadores de energia de estados intermediários.
As equações diferenciais acopladas da teoria de perturbação de primeira ordem para o estado em estudo ![]() e estados intermediários
e estados intermediários ![]() podem ser resolvidas para a correção de energia própria.
podem ser resolvidas para a correção de energia própria.
O resultado é, em geral, complexo. A parte imaginária da correção da energia própria está diretamente relacionada à largura do estado.
A dependência do tempo da função de onda para o estado ![]() é modificada pela correção de energia própria .
é modificada pela correção de energia própria .
Isso nos dá o comportamento de decaimento exponencial que esperamos, evitando que as seções transversais de espalhamento ressonante cheguem ao infinito .
A parte real da correção deve ser estudada para compreender as mudanças relativas de energia dos estados. É a diferença entre a energia própria do elétron ligado e a de um elétron livre na qual estamos interessados. A correção de autoenergia para uma partícula livre pode ser calculada.
Nós automaticamente contabilizamos essa correção por uma mudança na massa observada do elétron. Para a definição não relativística da energia de um elétron livre, um aumento na massa diminui a energia.
Se cortarmos a integral em 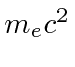 , a correção da massa é de apenas cerca de 0,3% ,
, a correção da massa é de apenas cerca de 0,3% ,
Uma vez que a massa observada do elétron já é responsável pela maior parte da correção de energia própria para um estado ligado, devemos corrigir esse efeito para evitar a contagem dupla da correção. A correção de energia própria para um estado limitado então é.
Em 1947, Willis E. Lamb e RC Retherford usaram técnicas de microondas para determinar a divisão entre os estados 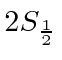 e
e 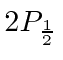 no hidrogênio . O resultado pode ser bem explicado pela correção da energia própria, pelo menos quando a mecânica quântica relativística é usada. Nosso cálculo não relativístico fornece uma explicação qualitativa do efeito.
no hidrogênio . O resultado pode ser bem explicado pela correção da energia própria, pelo menos quando a mecânica quântica relativística é usada. Nosso cálculo não relativístico fornece uma explicação qualitativa do efeito.
A Equação de Dirac
Nosso objetivo é encontrar o análogo da equação de Schrödinger para partículas relativísticas de spin meio, entretanto, devemos notar que mesmo na equação de Schrödinger, a interação do campo com o spin era bastante ad hoc. Não houve explicação da razão giromagnética de 2. Pode-se incorporar o spin na equação não relativística usando o hamiltoniano de Schrödinger-Pauli que contém o produto escalar das matrizes de Pauli com o operador momentum.
Um pequeno cálculo mostra que isso dá a interação correta com o spin.
Este hamiltoniano atua em um spinor de dois componentes.
Podemos estender este conceito para usar a equação da energia relativística . A ideia é substituir ![]() com na equação da energia relativística.
com na equação da energia relativística. 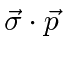
Em vez de uma equação de segunda ordem na derivada do tempo, podemos fazer uma equação de primeira ordem, como a equação de Schrödinger, estendendo essa equação para quatro componentes.
Agora reescrevendo em termos de e e ordenando-o como uma equação de matriz, obtemos uma equação que pode ser escrita como um produto escalar entre 4 vetores. 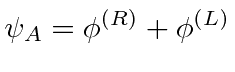
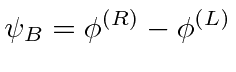
Defina as matrizes 4 por 4 ![]() por.
por.
Com esta definição, a equação relativística pode ser bastante simplificada
onde as matrizes gama são dadas por
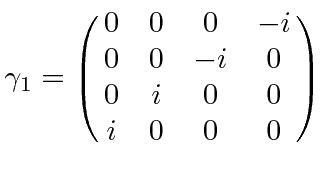 |
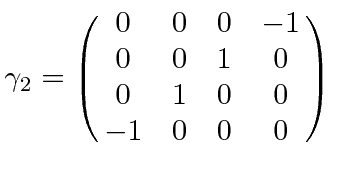 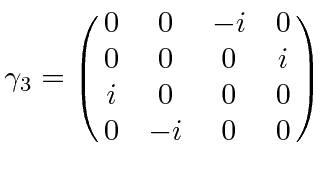 |
e eles satisfazem as relações anti-comutação.
Na verdade, qualquer conjunto de matrizes que satisfaça as relações anticomutação produziria resultados físicos equivalentes, no entanto, trabalharemos na representação explícita acima das matrizes gama.
satisfaz a equação de uma corrente conservada de 4 vetores
e também se transforma como um vetor 4. O quarto componente do vetor mostra que a densidade de probabilidade é . Isso indica que a normalização do estado inclui todos os quatro componentes dos espinores de Dirac. 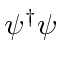
Para elétrons não relativísticos, os dois primeiros componentes do espinor de Dirac são grandes, enquanto os dois últimos são pequenos.
Usamos esse fato para escrever uma equação aproximada de dois componentes derivada da equação de Dirac no limite não relativístico.
Esta `` equação de Schrödinger '', derivada da equação de Dirac , concorda bem com a que usamos para entender a estrutura fina do Hidrogênio. Os primeiros dois termos são os termos de energia cinética e potencial para o hamiltoniano de hidrogênio não perturbado. O terceiro termo é a correção relativística da energia cinética . O quarto termo é a interação spin-órbita correta , incluindo o efeito Thomas Precession que não perdemos tempo para entender quando fizemos a estrutura fina NR. O quinto termo é o assim chamado termo de Darwin, que dissemos vir da equação de Dirac; e agora está.
Para uma partícula livre, cada componente do spinor de Dirac satisfaz a equação de Klein-Gordon.
Isso é consistente com a relação de energia relativística.
As quatro soluções normalizadas para uma partícula de Dirac em repouso são.
O primeiro e o terceiro giram para cima, enquanto o segundo e o quarto giram para baixo. A primeira e a segunda são soluções de energia positiva, enquanto a terceira e a quarta são `` soluções de energia negativa '' , que ainda precisamos entender.
O próximo passo é encontrar as soluções com momentum definido. As quatro soluções de ondas planas para a equação de Dirac são
onde os quatro espinores são dados por.
![]() é positivo para as soluções 1 e 2 e negativo para as soluções 3 e 4. Os espinores são ortogonais
é positivo para as soluções 1 e 2 e negativo para as soluções 3 e 4. Os espinores são ortogonais
e as constantes de normalização foram definidas para que os estados sejam normalizados corretamente e os spinors sigam a convenção dada acima, com a normalização proporcional à energia.
As soluções não são em geral estados próprios de qualquer componente do spin, mas são estados próprios de helicidade , o componente do spin ao longo da direção do momento.
Observe que com o ![]() negativo, o exponencial tem a velocidade de fase, a velocidade do grupo e o fluxo de probabilidade, todos na direção oposta do momento como o definimos. Isso claramente não faz sentido. As soluções 3 e 4 precisam ser entendidas de uma forma para a qual os operadores não relativísticos não nos prepararam. Vamos simplesmente renomear as soluções 3 e 4 de forma que
negativo, o exponencial tem a velocidade de fase, a velocidade do grupo e o fluxo de probabilidade, todos na direção oposta do momento como o definimos. Isso claramente não faz sentido. As soluções 3 e 4 precisam ser entendidas de uma forma para a qual os operadores não relativísticos não nos prepararam. Vamos simplesmente renomear as soluções 3 e 4 de forma que ![]()
de forma que todas as energias são positivas e os momentos apontam na direção das velocidades. Isso significa que alteramos os sinais nas soluções 3 e 4 da seguinte maneira.
Temos ondas planas da forma
com o sinal de mais para as soluções 1 e 2 e o sinal de menos para as soluções 3 e 4. Esses ![]() sinais no exponencial não são muito surpreendentes do ponto de vista das soluções possíveis para uma equação diferencial. O problema agora é que para as soluções 3 e 4 os operadores de momentum e energia devem ter um sinal negativo adicionado a eles e a fase da função de onda em uma posição fixa se comporta de maneira oposta em função do tempo do que esperamos e de soluções 1 e 2. É como se as soluções 3 e 4 estivessem retrocedendo no tempo.
sinais no exponencial não são muito surpreendentes do ponto de vista das soluções possíveis para uma equação diferencial. O problema agora é que para as soluções 3 e 4 os operadores de momentum e energia devem ter um sinal negativo adicionado a eles e a fase da função de onda em uma posição fixa se comporta de maneira oposta em função do tempo do que esperamos e de soluções 1 e 2. É como se as soluções 3 e 4 estivessem retrocedendo no tempo.
Se mudarmos a carga do elétron de ![]() para
para ![]() e mudarmos o sinal do expoente, a equação de Dirac permanece invariante. Assim, podemos transformar a solução do expoente negativo (retrocedendo no tempo) na solução do expoente positivo convencional se mudarmos a carga para
e mudarmos o sinal do expoente, a equação de Dirac permanece invariante. Assim, podemos transformar a solução do expoente negativo (retrocedendo no tempo) na solução do expoente positivo convencional se mudarmos a carga para ![]() . Podemos interpretar as soluções 3 e 4 como pósitrons. Faremos essa mudança com mais cuidado quando estudarmos o operador de conjugação de carga.
. Podemos interpretar as soluções 3 e 4 como pósitrons. Faremos essa mudança com mais cuidado quando estudarmos o operador de conjugação de carga.
A equação de Dirac deve ser invariante sob impulsos de Lorentz e rotações, sendo que ambos são apenas mudanças na definição de um sistema de coordenadas inercial. Sob aumentos de Lorentz, transforma-se como um vetor 4, mas as matrizes são constantes. A equação de Dirac mostra-se invariante sob impulsos ao longo da direção se transformarmos o espinor de Dirac de acordo com 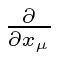
![]()
![]()
A equação de Dirac é invariante em rotações em torno do ![]() eixo se transformarmos o espinor de Dirac de acordo com
eixo se transformarmos o espinor de Dirac de acordo com
Outra simetria relacionada à escolha do sistema de coordenadas é a paridade. Sob uma operação de inversão de paridade, a equação de Dirac permanece invariante se
Desde então , o terceiro e o quarto componentes do spinor mudam de sinal, enquanto os dois primeiros não. Como poderíamos ter escolhido , tudo o que sabemos é que os componentes 3 e 4 têm a paridade oposta dos componentes 1 e 2 . 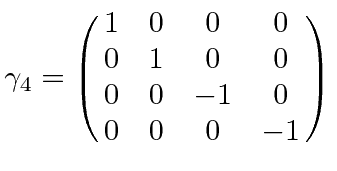
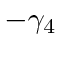
De 4 por 4 matrizes, podemos derivar 16 componentes independentes de objetos covariantes. Nós definir o produto de todas as matrizes gama .
que obviamente anticomuta com todas as matrizes gama.
Para rotações e impulsos, ![]() comuta com,
comuta com, ![]() pois comuta com o par de matrizes gama. Para uma inversão de paridade, é anti-mudo com
pois comuta com o par de matrizes gama. Para uma inversão de paridade, é anti-mudo com 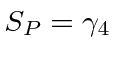 .
.
O conjunto mais simples de covariantes que podemos fazer a partir de espinores e ![]() matrizes de Dirac estão tabulados abaixo.
matrizes de Dirac estão tabulados abaixo.
| Classificação | Forma covariante | não. de componentes |
| Escalar | 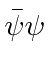 |
1 |
| Pseudoescalar | 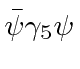 |
1 |
| Vetor | 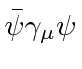 |
4 |
| Vetor Axial | 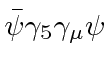 |
4 |
| Tensor antissimétrico de Rank 2 | 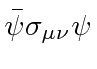 |
6 |
| Total | 16 |
Produtos de mais ![]() matrizes acabam repetindo as mesmas quantidades porque o quadrado de qualquer
matrizes acabam repetindo as mesmas quantidades porque o quadrado de qualquer ![]() matriz é 1.
matriz é 1.
Para muitos propósitos, é útil escrever a equação de Dirac na forma tradicional 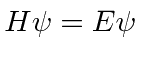 . Para fazer isso, devemos separar as derivadas de espaço e tempo, tornando a equação menos covariante.
. Para fazer isso, devemos separar as derivadas de espaço e tempo, tornando a equação menos covariante.
Assim, podemos identificar o operador abaixo como o Hamiltoniano.
O hamiltoniano nos ajuda a identificar constantes do movimento. Se um operador comuta com ![]() , ele representa uma quantidade conservada.
, ele representa uma quantidade conservada.
É fácil ver o ![]() trajeto com o hamiltoniano para uma partícula livre, de modo que o momentum seja conservado . Os componentes do momento angular orbital não comutam com
trajeto com o hamiltoniano para uma partícula livre, de modo que o momentum seja conservado . Os componentes do momento angular orbital não comutam com ![]() .
.
Os componentes do spin também não comutam com ![]() .
.
Mas, do acima exposto, os componentes do momento angular total comutam com ![]() .
.
A equação de Dirac naturalmente conserva o momento angular total, mas não as partes orbitais ou de spin dele.
Também podemos ver que a helicidade , ou giro ao longo da direção do movimento, comuta.
Para qualquer cálculo, precisamos saber o termo de interação com o campo eletromagnético. Com base na interação do campo com uma corrente
e a corrente que encontramos para a equação de Dirac, o hamiltoniano de interação é.
Isso é mais simples do que o caso não relativístico, sem ![]() termo e apenas uma potência de
termo e apenas uma potência de ![]() .
.
A equação de Dirac tem alguns fenômenos inesperados que podemos derivar. Os autovalores de velocidade para elétrons estão sempre ![]() ao longo de qualquer direção. Portanto, os únicos valores de velocidade que podemos medir são
ao longo de qualquer direção. Portanto, os únicos valores de velocidade que podemos medir são ![]() .
.
Estados localizados, expandidos em ondas planas, contêm todos os quatro componentes das soluções de ondas planas. A mistura dos componentes 1 e 2 com os componentes 3 e 4 dá origem a Zitterbewegung , a oscilação muito rápida da velocidade e posição dos elétrons.
A última soma que contém os termos cruzados entre energia negativa e positiva representa oscilações de frequência extremamente altas no valor esperado da velocidade , conhecido como Zitterbewegung. O valor esperado da posição tem oscilações rápidas semelhantes.
É possível resolver a equação de Dirac exatamente para o hidrogênio de uma forma muito semelhante à solução não relativística. Uma diferença é que está claro desde o início que o momento angular total é uma constante do movimento e é usado como um número quântico básico. Há outro número quântico conservado relacionado ao componente de spin ao longo da direção de ![]() . Com esses números quânticos, a equação radial pode ser resolvida de maneira semelhante ao caso não relativístico que produz a relação de energia .
. Com esses números quânticos, a equação radial pode ser resolvida de maneira semelhante ao caso não relativístico que produz a relação de energia .
Podemos identificar o número quântico do princípio padrão neste caso como . Esse resultado fornece a mesma resposta que nosso cálculo não relativístico para ordem, mas também está correto para ordem superior . É uma solução exata para o problema de mecânica quântica proposto, mas não inclui os efeitos da teoria de campos , como o deslocamento de Lamb e o momento magnético anômalo do elétron. 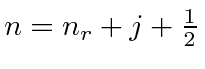
![]()
Um cálculo de espalhamento Thomson mostra que mesmo o espalhamento simples de fótons de baixa energia depende da "energia negativa" ou estados de pósitron para obter uma resposta diferente de zero. Se o cálculo for feito com os dois diagramas em que um fóton é absorvido e depois emitido por um elétron (e vice-versa), o resultado é zero em baixa energia porque a interação hamiltoniana conecta o primeiro e o segundo estados de onda plana com o terceiro e o quarto em momento zero. Isso está em contradição com os cálculos clássicos e não relativísticos, bem como com a medição. Existem diagramas adicionais se considerarmos a possibilidade de que o fóton pode criar um par de pósitrons de elétrons que se aniquila com o elétron inicial emitindo um fóton (ou com os fótons inicial e final trocados). Esses dois termos fornecem a resposta certa.
A equação de Dirac é invariante sob a conjugação de carga, definida como a mudança dos estados do elétron para os estados de pósitrons carregados opostos com o mesmo momento e spin (e mudança do sinal dos campos externos). Para fazer isso, o spinor de Dirac é transformado de acordo com.
É claro que uma segunda operação de conjugação de carga leva o estado de volta ao original ![]() . Aplicar isso às soluções de onda plana dá
. Aplicar isso às soluções de onda plana dá
que define novos espinores de pósitrons e que são conjugados de carga de e . 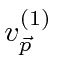
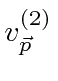
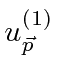
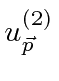
A Equação de Dirac
Para prosseguir em direção a uma teoria de campo para elétrons e quantização do campo de Dirac, desejamos encontrar um Lagrangiano escalar que produza a equação de Dirac. A partir do estudo das covariantes de Lorentz, sabemos que é um escalar e que podemos formar um escalar a partir do produto escalar de dois 4 vetores como no Lagrangiano abaixo. O Lagrangiano não pode depender explicitamente das coordenadas. 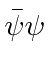
(Também poderíamos adicionar um termo tensorial, mas não é necessário para obter a equação de Dirac.) Os campos independentes são considerados os 4 componentes de ![]() e os quatro componentes de
e os quatro componentes de ![]() . A equação de Euler-Lagrange usando os
. A equação de Euler-Lagrange usando os ![]() campos independentes é simples, pois não há derivada de
campos independentes é simples, pois não há derivada de ![]() no Lagrange.
no Lagrange.
Isso nos dá a equação de Dirac indicando que este Lagrangiano é o correto. A equação de Euler-Lagrange derivada usando os campos ![]() é a equação adjunta de Dirac ,
é a equação adjunta de Dirac ,
A densidade Hamiltoniana pode ser derivada da Lagrangiana na forma padrão e a Hamiltoniana total calculada pela integração no espaço. Observe que a densidade hamiltoniana é a mesma que a hamiltoniana derivada da equação de Dirac diretamente.
Podemos expandir ![]() em ondas planas para entender o hamiltoniano como uma soma de osciladores.
em ondas planas para entender o hamiltoniano como uma soma de osciladores.
Escrevendo o hamiltoniano em termos desses campos , a fórmula pode ser simplificada, resultando
Por analogia com o eletromagnetismo, podemos substituir os coeficientes de Fourier para as ondas planas de Dirac por operadores.
A criação de uma operadores de aniquilação e Satisfazer as relações anticomutadoras. 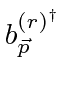
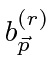
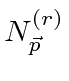 é o operador do número de ocupação. As relações anti-comutação restringem o número de ocupação a 1 ou 0 .
é o operador do número de ocupação. As relações anti-comutação restringem o número de ocupação a 1 ou 0 .
O campo de Dirac e o hamiltoniano podem agora ser reescritos em termos de campos de elétron e pósitron para os quais a energia é sempre positiva, substituindo o operador para aniquilar um `` estado de energia negativa '' por um operador para criar um estado de pósitron com o momento certo e rodar.
Estes anti-comutação com tudo o mais, exceto que
Agora reescreva os campos e o hamiltoniano.
Todas as energias desses estados são positivas .
Existe uma energia constante (infinita), semelhante mas de sinal oposto ao do campo EM quantizado, que devemos adicionar para fazer com que o estado de vácuo tenha energia zero. Observe que, se tivéssemos usado operadores de deslocamento (Bose-Einstein) em vez de anti-deslocamento, não haveria estado fundamental de energia mais baixa, de modo que essa subtração de energia não teria sido possível. As estatísticas de Fermi-Dirac são necessárias para partículas que satisfaçam a equação de Dirac .
Uma vez que os operadores que criam estados de férmions são anti-comutação , os estados de férmions devem ser anti-simétricos sob o intercâmbio. Assuma ![]() e
e ![]() são os operadores de criação e aniquilação de férmions e que eles anti-comutam.
são os operadores de criação e aniquilação de férmions e que eles anti-comutam.
Os estados são então anti-simétricos sob intercâmbio de pares de férmions.
Não é difícil mostrar que o número de ocupação para estados de férmions é zero ou um .
Observe que os spinors satisfazem as seguintes equações ligeiramente diferentes .
Feynman Lectures, Volume III, Capítulo I.
Gasciorawicz realmente não faz isso.
Capítulos 5 de Rohlf
Griffiths não cobre isso.
Difração de Duas Fendas
As ondas de água exibirão um padrão de interferência difrativa em um experimento de 2 fendas, conforme diagramado abaixo. O diagrama mostra as cristas das ondas de água em algum momento. A jusante das fendas, veremos a interferência construtiva onde as ondas das fendas estão em fase e a interferência destrutiva onde estão 180 graus defasados, por exemplo, onde uma crista de uma fenda encontra uma depressão da outra. O gráfico marcado ![]() mostra o padrão de interferência no local do absorvedor. A difração é um fenômeno de onda simples .
mostra o padrão de interferência no local do absorvedor. A difração é um fenômeno de onda simples .
A difração da luz era um fenômeno bem conhecido no final do século 19 e era bem explicado na teoria eletromagnética clássica, uma vez que a luz era considerada uma onda EM. O padrão de difração de duas fendas estreitas é particularmente fácil de entender em termos de ondas. A configuração é mostrada no diagrama abaixo.
As ondas EM de comprimento de onda ![]() são emitidas por uma única fonte de luz, como um laser. Eles viajam para duas fendas estreitas, (para simplificar) equidistantes da fonte e a uma distância uma da
são emitidas por uma única fonte de luz, como um laser. Eles viajam para duas fendas estreitas, (para simplificar) equidistantes da fonte e a uma distância uma da ![]() outra. A luz viaja das fendas para uma tela de detecção. Um padrão de difração pode ser visto na tela de detecção, como o mostrado na imagem abaixo.
outra. A luz viaja das fendas para uma tela de detecção. Um padrão de difração pode ser visto na tela de detecção, como o mostrado na imagem abaixo.
O centro do padrão de difração ocorre no local da tela equidistante de cada fenda onde as ondas das duas fendas estão em fase (porque elas viajaram exatamente a mesma distância) e os campos se somam, então as ondas interferem construtivamente e há um máximo de intensidade. A alguma distância deste centro do padrão de difração, haverá interferência destrutiva entre as ondas das duas fendas e a intensidade será zero. Isso ocorrerá quando a distância percorrida por duas ondas for diferente em 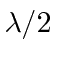 , então as ondas estão 180 graus fora de fase e os campos das duas fendas se cancelam .
, então as ondas estão 180 graus fora de fase e os campos das duas fendas se cancelam .
Podemos calcular esta localização observando o diagrama acima. Assumimos que a distância até a tela é muito maior do que ![]() . Para luz detectada em um ângulo
. Para luz detectada em um ângulo ![]() , a distância extra percorrida desde a fenda 1 é justa
, a distância extra percorrida desde a fenda 1 é justa ![]() . Portanto, o ângulo do primeiro mínimo (ou nulo) pode ser encontrado na equação .
. Portanto, o ângulo do primeiro mínimo (ou nulo) pode ser encontrado na equação . 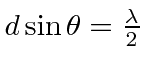
De maneira mais geral, obteremos um máximo se os caminhos das fendas diferirem em um número inteiro de comprimentos de onda e obteremos um valor nulo quando os caminhos diferirem em meio número inteiro de comprimentos de onda . . ![]()
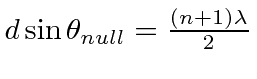
Embora seja muito difícil porque os elétrons estão carregados, a difração de elétrons de 2 fendas também foi observada.
Assim, todos os tipos de partículas parecem difratar, indicando que há algum tipo de onda envolvida. Vamos agora continuar com alguns experimentos mentais sobre difração para ilustrar a física que a Mecânica Quântica precisava corresponder.Difração de fenda única
Existem muitos outros exemplos de difração. A imagem abaixo mostra a difração de uma única fenda onde ondas de diferentes partes da fenda interferem umas nas outras. Para obter o campo em algum ponto da tela de detecção, deve-se integrar sobre a fenda.
* Exemplo: derivar a localização dos nós no padrão de difração de uma fenda de largura ![]() . Agora tente calcular a distribuição de intensidade para difração de fenda única. *
. Agora tente calcular a distribuição de intensidade para difração de fenda única. *
* Exemplo: derivar a localização dos nós no padrão de difração de duas fendas estreitas a uma distância uma da ![]() outra. Agora tente calcular a distribuição de intensidade. *
outra. Agora tente calcular a distribuição de intensidade. *
Difração de fenda única
Existem muitos outros exemplos de difração. A imagem abaixo mostra a difração de uma única fenda onde ondas de diferentes partes da fenda interferem umas nas outras. Para obter o campo em algum ponto da tela de detecção, deve-se integrar sobre a fenda.
* Exemplo: derivar a localização dos nós no padrão de difração de uma fenda de largura ![]() . Agora tente calcular a distribuição de intensidade para difração de fenda única.
. Agora tente calcular a distribuição de intensidade para difração de fenda única.
Difração de Cristais
As ondas de elétrons foram demonstradas pela primeira vez medindo a difração de cristais . Davison e Germer observaram a difração de elétrons de um cristal de níquel em 1928. Eles variaram a energia do elétron para medir o comprimento de onda do elétron, concordando bem com a expectativa de deBroglie.
Primeiro, vemos a difração de um único cristal .
A difração de material policristalino dá anéis concêntricos em vez de pontos.
A difração de cristais é uma ferramenta poderosa. Primeiro, vemos a difração de raios-X de um único cristal de sódio que tem localizações periódicas dos átomos.
Outro exemplo de difração é mostrado abaixo. Aqui os nêutrons difratam de um único cristal de sódio .
O comprimento de onda DeBroglie
A transformação de Lorentz foi postulada para ondas eletromagnéticas antes de Einstein desenvolver a relatividade especial. As ondas EM eram inteiramente consistentes com a Relatividade. Por exemplo, a fase de uma onda EM em algum ponto é a mesma do ponto transformado de Lorentz.DeBroglie aplicou este requisito de invariância de Lorentz na fase das ondas de matéria para determinar qual deve ser o comprimento de onda. É fácil para nós derivar o comprimento de onda usando 4 vetores. Posição e tempo formam um vetor 4.
Energia e impulso formam outro.
Lembre-se de que os vetores de Lorentz devem ser transformados, mas os escalares de Lorentz são automaticamente invariantes sob transformações. Por exemplo, o escalar formado pontuando o momento 4 em si mesmo é
A massa de uma partícula é claramente invariante de Lorentz.
Para calcular o comprimento de onda de nossas ondas de matéria, vamos usar o escalar
Já é fácil ver que a fase de uma onda como
é invariante de Lorentz.
Para ler o comprimento de onda, vamos escolher a parte da expressão que corresponde a . Vemos isso e, portanto, o comprimento de onda DeBroglie é. ![]()
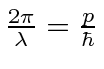
Também podemos ler a frequência ![]() .
.
Em certo sentido, essa foi a entrada para o nosso cálculo.
O comprimento de onda deBroglie será nosso principal input de física para o desenvolvimento da Mecânica Quântica. Não é que este trabalho tenha sido o mais significativo, mas este comprimento de onda resume a maior parte do que aconteceu antes de 1923.
Computando comprimentos de onda DeBroglie
Costumamos citar a energia de uma partícula em termos de sua energia cinética em Volts, eV do elétron (ou Volts do Milhão de elétrons, MeV). A razão para isso é que as partículas são geralmente aceleradas para alguma energia por um campo elétrico. Se eu deixar um elétron (ou próton ...) ser acelerado por uma diferença de potencial de 100 Volts, ele terá uma energia cinética de 100eV.
Todo o problema de calcular um comprimento de onda deBroglie é converter a energia cinética em momento. Se você sempre quer estar correto sem nenhuma necessidade de pensar, use a fórmula relativisticamente correta para a energia cinética
em seguida, use esta fórmula útil para obter a resposta.
Lembro-me disso permitindo-me manter todo o cálculo em eV. Eu também conheço as massas das partículas. ![]()
(Se 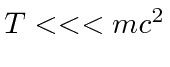 , certifique-se de que a precisão de sua calculadora é suficiente ou use o método não relativístico abaixo.)
, certifique-se de que a precisão de sua calculadora é suficiente ou use o método não relativístico abaixo.)
Se você sabe que a partícula é super-relativista , de modo que 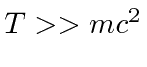 , em seguida, basta usar
, em seguida, basta usar 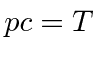 ea vida é fácil.
ea vida é fácil.
Se você sabe que a partícula é altamente não-relativista , 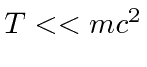 , então você pode usar doação .
, então você pode usar doação . 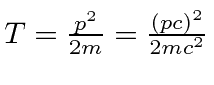
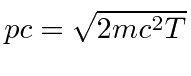
Então, por exemplo, calcule o comprimento de onda de um elétron de 100 eV. Isso é não relativístico, pois 100 eV «510000 eV. Então eV ou 10000 eV. 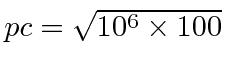
Dualidade de partícula de onda (experimentos de pensamento)
Richard Feynman (Prêmio Nobel de Eletrodinâmica Quântica ...) apresenta vários experimentos mentais em suas Lectures on Physics, terceiro volume.
Para nosso primeiro experimento mental, consideraremos duas difração de luz de silte . Suponha que, em vez de usar a tela, eu use um fotodetector sensível . Medo a intensidade da luz em função da posição perto da tela e encontro o mesmo conjunto de máximos e mínimos que fiz usando meus olhos.
Agora vamos diminuir a intensidade da fonte de luz. Para intensidade muito baixa, acho que meu detector coleta um fóton por vez . Nunca coleta meio fóton. (Com o detector certo, eu poderia verificar novamente que, para cada fóton, o efeito fotoelétrico é visto e tal ![]() .) Então as ondas que estão difratando são de alguma forma formadas por fótons. Com uma intensidade suficientemente baixa , posso garantir que apenas um fóton está presente no aparelho por vez. Posso operar meu detector e coletar dados por um longo tempo, somando o número de fótons detectados em função da posição. O que vou receber pela distribuição? Eu obtenho exatamente a mesma distribuição de antes com máximos e mínimos. Não importa quão baixa seja a intensidade, (1 partícula / minuto!)ainda vemos difração . Nunca detectamos uma fração de um elétron ou um fóton, apenas números inteiros .
.) Então as ondas que estão difratando são de alguma forma formadas por fótons. Com uma intensidade suficientemente baixa , posso garantir que apenas um fóton está presente no aparelho por vez. Posso operar meu detector e coletar dados por um longo tempo, somando o número de fótons detectados em função da posição. O que vou receber pela distribuição? Eu obtenho exatamente a mesma distribuição de antes com máximos e mínimos. Não importa quão baixa seja a intensidade, (1 partícula / minuto!)ainda vemos difração . Nunca detectamos uma fração de um elétron ou um fóton, apenas números inteiros .
Como um único fóton interfere em si mesmo? Deve de alguma forma passar por ambas as fendas.
Vamos voltar para a difração de elétrons por um minuto. Em nosso experimento mental, novamente temos duas fendas.
Usamos nosso detector para medir o padrão de difração semelhante ao dos fótons rotulados 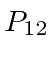 abaixo. Se cobrirmos a fenda 2 , obteremos a distribuição rotulada
abaixo. Se cobrirmos a fenda 2 , obteremos a distribuição rotulada ![]() e se / emphtextcovermos a fenda 1 obtermos a distribuição de intensidade rotulada
e se / emphtextcovermos a fenda 1 obtermos a distribuição de intensidade rotulada ![]() . Poderíamos ter feito o mesmo com nossos fótons acima.
. Poderíamos ter feito o mesmo com nossos fótons acima.
Agora tentaremos ver por qual fenda cada elétron passa. Colocamos uma fonte de luz brilhante perto das fendas e detectamos a luz refletida no elétron para que possamos ver por qual fenda ele passa.
Que distribuição vemos agora? Na verdade, veremos 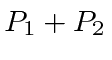 se podemos dizer por qual fenda o elétron passou. Nossa observação do elétron ao passar pela fenda mudou a distribuição de intensidade resultante . Se desligarmos a luz, voltamos a medir
se podemos dizer por qual fenda o elétron passou. Nossa observação do elétron ao passar pela fenda mudou a distribuição de intensidade resultante . Se desligarmos a luz, voltamos a medir 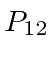 .
.
Você pode explicar por que a luz faz com que o padrão de difração desapareça?
É a mera observação? A luz muda a fase do elétron?
Existem muitos exemplos de um observador alterando o resultado de um experimento Quantum. Na verdade, é sustentado que quando um estado é observado, sua função de onda colapsa no estado `` visto ''. Nesse caso, bastava acender a luz. Não precisamos olhar.
Finalmente, faremos um experimento de difração de duas fendas com balas . Devemos fazer fendas grandes o suficiente para as balas passarem.
Não importa a distância entre as fendas que escolhemos, nunca observamos difração para as balas. Eles sempre fornecem o 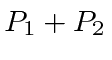 padrão (provavelmente diferente para os marcadores). Você pode explicar isso?
padrão (provavelmente diferente para os marcadores). Você pode explicar isso?
O comprimento de onda da bala é muito menor do que o tamanho real da bala.
Por que não vimos difração para as balas. As balas são objetos macroscópicos com grandes momentos em comparação com partículas individuais. O momento elevado implica um pequeno comprimento de onda deBroglie. Portanto, para ver a difração, devemos tornar a distância entre as fendas muito menor do que fizemos para os fótons (talvez ![]() vezes menor). Mas as balas também são grandes. Eles só passam por grandes fendas, que devem estar mais afastadas do que as fendas usadas para os fótons. Para balas, o comprimento de onda é minúsculo em comparação com qualquer fenda pela qual uma bala passaria . Portanto, nenhuma difração de bala é possível.
vezes menor). Mas as balas também são grandes. Eles só passam por grandes fendas, que devem estar mais afastadas do que as fendas usadas para os fótons. Para balas, o comprimento de onda é minúsculo em comparação com qualquer fenda pela qual uma bala passaria . Portanto, nenhuma difração de bala é possível.
Feynman Lectures on Physics, Vol. III Capítulo 1
Exemplos
Distribuição de intensidade para difração de duas fendas *
Derive a localização dos nós no padrão de difração a partir de duas fendas estreitas ![]() separadas por uma distância . Agora tente calcular a distribuição de intensidade.
separadas por uma distância . Agora tente calcular a distribuição de intensidade.
Este é um exercício de laboratório .
Distribuição de intensidade para difração de fenda única *
Derive a localização dos nós no padrão de difração de uma fenda de largura ![]() . Agora tente calcular a distribuição de intensidade para difração de fenda única.
. Agora tente calcular a distribuição de intensidade para difração de fenda única.
Este é um exercício de laboratório .
Problemas de teste de amostra
- Qual é o comprimento de onda deBroglie de um elétron com 13,6 eV de energia cinética? Qual é o comprimento de onda deBroglie de um elétron com 10 MeV de energia cinética?
A resposta
13.6 eV é muito menor, então isso não é relativístico.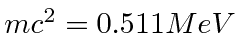
10 MeV é muito maior do que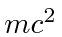 um elétron, então é super-relativístico e podemos usar
um elétron, então é super-relativístico e podemos usar 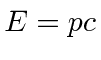 .
.
- Qual é o comprimento de onda DeBroglie para cada uma das seguintes partículas? As energias fornecidas são as energias cinéticas.
- a)
- um elétron de 10 eV
- b)
- um elétron de 1 MeV
- c)
- um próton de 10 MeV
- Um experimento de difração de elétrons de 2 fendas é configurado como (não) mostrado abaixo. A distribuição de intensidade de elétrons observada é plotada na figura. Agora, uma fonte de luz intensa é introduzida perto das duas fendas. Com esta luz, pode-se "ver" por qual fenda cada elétron passa. Faça um gráfico qualitativo da nova distribuição de intensidade do elétron de cada fenda e das 2 fendas combinadas. Qual é a condição do comprimento de onda da luz para que esse efeito ocorra?
- Qual é o comprimento de onda DeBroglie para cada uma das seguintes partículas? As energias fornecidas são as energias cinéticas.
- Qual KE deve ter um átomo de hidrogênio para que seu comprimento de onda DeBroglie seja menor que o tamanho do átomo? (Fatores de 2 não são importantes.)
- Calcule o comprimento de onda DeBroglie para (a) um próton com energia cinética de 10 MeV, (b) Um elétron com energia cinética de 10 MeV e (c) uma bola de chumbo de 1 grama movendo-se com uma velocidade de 10 cm / s (um erg é um grama cm
 / seg
/ seg 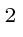 ). Certifique-se de levar em conta a relatividade quando necessário.
). Certifique-se de levar em conta a relatividade quando necessário.
No final do século XIX, as leis da física baseavam-se na mecânica e na lei da gravitação de Newton, nas equações de Maxwell que descreviam a eletricidade e o magnetismo e na mecânica estatística que descrevia o estado de uma grande coleção de matéria. Essas leis da física descreveram a natureza muito bem na maioria das condições, no entanto, algumas medições do final do século 19 e início do século 20 não puderam ser compreendidas. Os problemas com a física clássica levaram ao desenvolvimento da Mecânica Quântica e da Relatividade Especial.
Alguns dos problemas que levaram ao desenvolvimento da Mecânica Quântica estão listados aqui.
- Radiação de corpo negro: a física clássica previu que objetos quentes irradiariam instantaneamente todo o seu calor em ondas eletromagnéticas. O cálculo, que foi baseado nas equações de Maxwell e na Mecânica Estatística, mostrou que a taxa de radiação foi para o infinito quando o comprimento de onda EM foi para zero, "A Catástrofe Ultravioleta". Plank resolveu o problema postulando que a energia EM foi emitida em quanta com
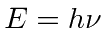 .
. - O efeito fotoelétrico: quando a luz foi usada para tirar os elétrons dos sólidos, os resultados foram completamente diferentes do que se esperava das equações de Maxwell. As medições eram fáceis de explicar (para Einstein) se a luz fosse composta de partículas com as energias postuladas por Plank.
- Átomos: Depois que Rutherford descobriu que a carga positiva nos átomos estava concentrada em um núcleo muito pequeno, a física clássica previu que os elétrons atômicos orbitando o núcleo irradiariam sua energia e entrariam em espiral no núcleo. Isso claramente não aconteceu. A energia irradiada pelos átomos também saiu em quantidades quantizadas em contradição com as previsões da física clássica. O átomo de Bohr postulou uma regra de quantização de momento angular,
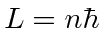 pois
pois  , isso deu o resultado certo para o hidrogênio, mas acabou se revelando errado, uma vez que o estado fundamental do hidrogênio tem momento angular zero. Foi necessário um conhecimento completo da Mecânica Quântica para explicar os espectros de energia atômica.
, isso deu o resultado certo para o hidrogênio, mas acabou se revelando errado, uma vez que o estado fundamental do hidrogênio tem momento angular zero. Foi necessário um conhecimento completo da Mecânica Quântica para explicar os espectros de energia atômica. - Espalhamento Compton: Quando a luz foi espalhada pelos elétrons, ela se comportou como uma partícula, mas muda o comprimento de onda no espalhamento; mais evidências para a natureza das partículas da luz e o postulado de Plank.
- Ondas e partículas: em experimentos de difração, a luz mostrou se comportar como uma onda, enquanto em experimentos como o efeito fotoelétrico, a luz se comportou como uma partícula. Experimentos de difração mais difíceis mostraram que os elétrons (assim como as outras partículas) também se comportavam como uma onda, mas só podemos detectar um número inteiro de elétrons (ou fótons).
A Mecânica Quântica incorpora uma dualidade onda-partícula e explica todos os fenômenos acima. Ao fazer isso, a Mecânica Quântica muda nossa compreensão da natureza de maneiras fundamentais. Enquanto as leis clássicas da física são determinísticas, QM é probabilística. Podemos apenas prever a probabilidade de uma partícula ser encontrada em alguma região do espaço.
Ondas eletromagnéticas como a luz são feitas de partículas que chamamos de fótons. Einstein, com base na fórmula de Plank, formulou a hipótese de que as partículas de luz tinham energia proporcional à sua frequência.
A nova ideia da Mecânica Quântica é que a probabilidade de cada partícula (em função da posição e do tempo) é igual ao quadrado de uma função de amplitude de probabilidade e que essas amplitudes de probabilidade obedecem a uma equação de onda. É muito parecido com o caso do eletromagnetismo, onde a densidade de energia é como o quadrado do campo e, portanto, a densidade de probabilidade do fóton é como o quadrado do campo, embora o campo seja feito de ondas. Portanto, as amplitudes de probabilidade são como os campos que conhecemos do eletromagnetismo em muitos aspectos.
DeBroglie assumiu ![]() para fótons e outras partículas e usou a invariância de Lorentz (da relatividade especial) para derivar o comprimento de onda de partículas como elétrons.
para fótons e outras partículas e usou a invariância de Lorentz (da relatividade especial) para derivar o comprimento de onda de partículas como elétrons.
O resto da mecânica ondulatória foi construída em torno dessas idéias, dando uma imagem completa que poderia explicar as medições acima e poderia ser testada com uma precisão muito alta, particularmente no átomo de hidrogênio. Passaremos vários capítulos explorando essas idéias.
* Exemplo: Suponha que o fóton seja uma partícula com o comprimento de onda deBroglie padrão. Use a cinemática para derivar o comprimento de onda do fóton espalhado como uma função do ângulo para a dispersão de Compton. *
Gasiorowicz Capítulo 1
Capítulos Rohlf 3,6
Griffiths realmente não cobre isso.
Cohen-Tannoudji et al. Capítulo
Radiação de corpo negro *
Um corpo negro é aquele que absorve toda a radiação EM (luz ...) que o atinge. Para ficar em equilíbrio térmico, ele deve emitir radiação na mesma taxa em que a absorve, de modo que um corpo negro também irradie bem. (Fogões são pretos.)
A radiação de um objeto quente é familiar para nós. Objetos em torno da temperatura ambiente irradiam principalmente no infravermelho, como pode ser visto no gráfico abaixo.
Se aquecermos um objeto até cerca de 1.500 graus, começaremos a ver um brilho vermelho opaco e diremos que o objeto está incandescente. Se aquecermos algo até cerca de 5000 graus, perto da temperatura da superfície do Sol, ela irradia bem por todo o espectro visível e dizemos que é branco quente.
Ao considerar as placas em equilíbrio térmico, pode-se mostrar que a potência emissiva sobre o coeficiente de absorção deve ser a mesma em função do comprimento de onda, mesmo para placas de materiais diferentes.
Se houvesse diferenças, poderia haver um fluxo líquido de energia de uma placa para a outra, violando a condição de equilíbrio.
Um corpo negro é aquele que absorve toda a radiação incidente sobre ele.
Assim, o poder Emissivo do corpo negro,, 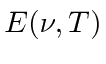 é universal e pode ser derivado dos primeiros princípios.
é universal e pode ser derivado dos primeiros princípios.
Um bom exemplo de corpo negro é uma cavidade com um pequeno orifício. Qualquer luz incidente sobre o orifício entra na cavidade e essencialmente nunca é refletida, uma vez que teria que sofrer um grande número de reflexos nas paredes da cavidade. Se tornarmos as paredes absorventes (talvez pintando-as de preto), a cavidade formará um corpo preto perfeito.
Há uma relação simples entre a densidade de energia em uma cavidade 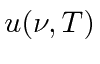 e o poder emissivo de corpo negro de um corpo negro que simplesmente vem de uma análise de quanta radiação, viajando na velocidade da luz, fluirá de um buraco no cavidade em um segundo.
e o poder emissivo de corpo negro de um corpo negro que simplesmente vem de uma análise de quanta radiação, viajando na velocidade da luz, fluirá de um buraco no cavidade em um segundo.
A única parte que requer um pouco de reflexão é o 4 na equação acima.
Rayleigh e Jeans calculado t ele densidade de energia (em ondas EM) no interior de uma cavidade e, por conseguinte, o espectro de emissão de um corpo negro. Seu cálculo foi baseado na teoria EM simples e equipartição. Não apenas não concordou com os dados; dizia que toda a energia seria irradiada instantaneamente em radiação EM de alta frequência. Isso foi chamado de catástrofe ultravioleta .
Plank encontrou uma fórmula que se ajusta bem aos dados em comprimentos de onda longos e curtos.
Sua fórmula se ajustou aos dados tão bem que ele tentou encontrar uma maneira de derivá-los. Em poucos meses, ele foi capaz de fazer isso, postulando que a energia era emitida em quanta com ![]() . Embora haja um grande número de modos de cavidade em alta frequência, a probabilidade de emitir tais quanta de alta energia desaparece exponencialmente de acordo com a distribuição de Boltzmann. Assim, Plank suprimiu a radiação de alta frequência no cálculo e concordou com o experimento. Observe que a fórmula de corpo negro de Plank é a mesma no limite que
. Embora haja um grande número de modos de cavidade em alta frequência, a probabilidade de emitir tais quanta de alta energia desaparece exponencialmente de acordo com a distribuição de Boltzmann. Assim, Plank suprimiu a radiação de alta frequência no cálculo e concordou com o experimento. Observe que a fórmula de corpo negro de Plank é a mesma no limite que 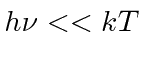 vai para zero em geral,
vai para zero em geral, ![]() enquanto a fórmula de Rayleigh vai para o infinito.
enquanto a fórmula de Rayleigh vai para o infinito.
É interessante notar que as ondas EM clássicas sugariam toda a energia térmica da matéria, tornando o universo um lugar muito frio para nós. A figura abaixo compara os dois cálculos com alguns dados em ![]() graus. (Também é surpreendente que o início da revolução quântica tenha vindo da radiação do corpo negro.)
graus. (Também é surpreendente que o início da revolução quântica tenha vindo da radiação do corpo negro.)
Portanto, a potência emissiva por unidade de área é
Podemos integrar isso sobre frequência para obter a potência total irradiada por unidade de área.
Exemplo: Qual é a temperatura na superfície solar? Use a intensidade da radiação na Terra e o pico do espectro em cerca de 500 nm para obter respostas. *
Exemplo: O fundo de micro-ondas cósmico é uma radiação de corpo negro com uma temperatura de 2,7 graus. Para qual frequência (e qual comprimento de onda) a intensidade atinge o pico? *
O efeito fotoelétrico
O efeito fotoelétrico mostra que a hipótese de Plank, usada para ajustar os dados do corpo negro, é realmente correta para a radiação EM. Einstein foi mais longe e propôs, em 1905, que a luz era composta de partículas com energia relacionada à frequência da luz ![]() . (Ele recebeu seu prêmio Nobel pelo efeito fotoelétrico, não por Relatividade Especial ou Geral.)
. (Ele recebeu seu prêmio Nobel pelo efeito fotoelétrico, não por Relatividade Especial ou Geral.)
Quando a luz atinge uma superfície polida (metal), os elétrons são ejetados.
As medições foram feitas da energia máxima do elétron versus frequência e intensidade da luz. A física clássica previu que a energia do elétron deveria aumentar com a intensidade, conforme o campo elétrico aumenta. Isso não é observado. A energia do elétron é independente da intensidade e depende linearmente da freqüência da luz, como pode ser visto na figura acima. A energia cinética dos elétrons é dada pela constante de Plank vezes a frequência da luz menos uma função de trabalho ![]() que depende do material.
que depende do material.
Esta equação apenas expressa a conservação da energia ![]() sendo a energia do fóton e
sendo a energia do fóton e ![]() a energia de ligação dos elétrons no sólido. Os dados do efeito fotoelétrico apoiaram fortemente a hipótese de que a luz é composta de partículas (fótons).
a energia de ligação dos elétrons no sólido. Os dados do efeito fotoelétrico apoiaram fortemente a hipótese de que a luz é composta de partículas (fótons).
O átomo de Rutherford *
A teoria clássica dos átomos afirmava que os elétrons estavam ligados a uma grande carga positiva do tamanho do átomo. Rutherford espalhou ![]() partículas carregadas ( ) dos átomos para ver qual era a distribuição de carga positiva. Com uma distribuição de carga aproximadamente uniforme, suas
partículas carregadas ( ) dos átomos para ver qual era a distribuição de carga positiva. Com uma distribuição de carga aproximadamente uniforme, suas ![]() partículas de 5,5 MeV nunca deveriam ter retrodifundido porque tinham energia suficiente para superar a força coulomb de uma distribuição de carga, essencialmente arando direto pelo meio.
partículas de 5,5 MeV nunca deveriam ter retrodifundido porque tinham energia suficiente para superar a força coulomb de uma distribuição de carga, essencialmente arando direto pelo meio.
Ele descobriu que as ![]() partículas costumavam se espalhar em ângulos maiores que 90 graus. Seus dados podem ser explicados se o núcleo positivo de um átomo for muito pequeno. Para um núcleo muito pequeno, a força de Coulomb continua a aumentar à medida que se
partículas costumavam se espalhar em ângulos maiores que 90 graus. Seus dados podem ser explicados se o núcleo positivo de um átomo for muito pequeno. Para um núcleo muito pequeno, a força de Coulomb continua a aumentar à medida que se ![]() aproxima do núcleo, e o retroespalhamento é possível.
aproxima do núcleo, e o retroespalhamento é possível.
Exemplo: Use a eletrostática para estimar o quão pequeno um núcleo de ouro deve ser para retroespalhar uma partícula alfa de 5,5 MeV. *
Isso trouxe um novo problema. O tamanho atômico era conhecido por vários tipos de experimentos. Se os elétrons orbitam em torno do núcleo atômico , de acordo com as equações de Maxwell, eles devem irradiar energia à medida que se aceleram. Esta radiação não é observada e os estados básicos dos átomos são estáveis.
Na Mecânica Quântica, a localização do elétron ao redor do núcleo é limitada por causa da natureza ondulatória do elétron . Para o hidrogênio, onde não há problema de múltiplos corpos para tornar o cálculo desnecessariamente difícil, os níveis de energia podem ser calculados com muita precisão. O hidrogênio foi usado para testar a mecânica quântica à medida que se desenvolvia. Também usaremos bastante hidrogênio neste curso.
O espalhamento das ![]() partículas de alta energia permitiu a Rutherford "ver" dentro do átomo e determinar que o núcleo atômico é muito pequeno. (Ele provavelmente destruiu todos os átomos que "viu".) A figura abaixo mostra a distribuição angular de Rutherford em seu experimento de espalhamento junto com vários usos subsequentes da mesma técnica, com partículas de energia cada vez mais altas. Vemos a descoberta de Rutherford do minúsculo núcleo , a descoberta da estrutura nuclear , a descoberta de um próton pontual dentro do núcleo , a descoberta da estrutura do próton , a descoberta de quarks dentro do próton e, finalmente, a falta de descoberta, até agora , de qualquerestrutura de quark .
partículas de alta energia permitiu a Rutherford "ver" dentro do átomo e determinar que o núcleo atômico é muito pequeno. (Ele provavelmente destruiu todos os átomos que "viu".) A figura abaixo mostra a distribuição angular de Rutherford em seu experimento de espalhamento junto com vários usos subsequentes da mesma técnica, com partículas de energia cada vez mais altas. Vemos a descoberta de Rutherford do minúsculo núcleo , a descoberta da estrutura nuclear , a descoberta de um próton pontual dentro do núcleo , a descoberta da estrutura do próton , a descoberta de quarks dentro do próton e, finalmente, a falta de descoberta, até agora , de qualquerestrutura de quark .
Para "ver'' essas coisas em distâncias cada vez menores, precisamos usar feixes de partículas com comprimento de onda cada vez menor e, portanto, com energia mais alta.
Espectro Atômico *
O hidrogênio foi, em última análise, o verdadeiro teste da teoria quântica. Medições de altíssima precisão foram feitas usando grades de difração. Estes foram bem compreendidos na QM não relativística e compreendidos ainda melhor na Teoria Quântica de Campos totalmente relativística, Eletrodinâmica Quântica.
A figura abaixo mostra os níveis de energia em hidrogênio , as transições entre os níveis de energia e o comprimento de onda da luz produzida na transição. A série Lyman cobre as transições para o estado fundamental e está além da parte visível do espectro. A série Balmer é devida a transições para o primeiro estado excitado e está no visível.
Na época de Plank ![]() , muitos dados existiam sobre as energias discretas nas quais os átomos irradiavam. Cada átomo tinha sua impressão digital de radiação única. Absorção em energias discretas também foi observada.
, muitos dados existiam sobre as energias discretas nas quais os átomos irradiavam. Cada átomo tinha sua impressão digital de radiação única. Absorção em energias discretas também foi observada.
A fórmula de Rydberg para as energias dos fótons emitidos pelo hidrogênio foi desenvolvida bem antes da explicação QM aparecer.
Alguns dos estados nos átomos mais pesados seguiram o mesmo tipo de fórmula. Melhores experimentos mostraram que as linhas espectrais eram freqüentemente divididas em um multipleto de linhas. Vamos entender essas divisões muito mais tarde no curso.
Átomos mais pesados fornecem um espectro ainda mais rico, mas são muito mais difíceis de calcular. Muito boas técnicas de aproximação foram desenvolvidas. Com computadores e boa técnica, os níveis de energia de átomos mais complexos podem ser calculados. O espectro de mercúrio mostrado abaixo tem muito mais linhas do que as vistas em hidrogênio.
A figura abaixo mostra a parte visível do espectro para várias fontes atômicas ou moleculares. Para o Hidrogênio, vemos principalmente a série Balmer, com uma linha da Paschen-Bach. Os espectros de diferentes átomos são bastante distintos. As moléculas têm muitos outros tipos de excitações e podem produzir muitas frequências de luz.
O átomo de Bohr
Bohr postulou que os elétrons orbitavam o núcleo como planetas orbitando o sol. Ele conseguiu ajustar os dados para o Hidrogênio postulando que os elétrons orbitavam o núcleo em órbitas circulares, e que o momento angular é quantizado de forma que ![]() , para
, para 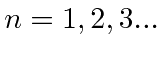 . Isso é natural, pois
. Isso é natural, pois ![]() tem unidades de momento angular. Bohr postou corretamente as energias do hidrogênio e o tamanho do átomo.
tem unidades de momento angular. Bohr postou corretamente as energias do hidrogênio e o tamanho do átomo.
Equilíbrio de forças para órbitas circulares.
Suposição de quantização de momento angular.
Resolva a velocidade.
Conecte a equação de força para obter a fórmula ![]() .
.
Agora queremos apenas conectar ![]() e
e ![]() entrar na fórmula de energia. Escrevemos o potencial de hidrogênio em termos da constante de estrutura fina .
entrar na fórmula de energia. Escrevemos o potencial de hidrogênio em termos da constante de estrutura fina . 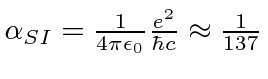
Agora calculamos os níveis de energia.
O eV constante . A fórmula de Bohr fornece o espectro de energia do hidrogênio correto .
Também podemos calcular o raio do estado fundamental da órbita de Bohr.
Isso também é sobre o raio certo. O nome desse número, raio de Bohr , persiste até hoje, apesar do fato de que a suposição de Bohr está errada.
Embora o momento angular seja quantizado em unidades de ![]() , o estado fundamental do Hidrogênio tem momento angular zero . Isso colocaria o elétron de Bohr no núcleo.
, o estado fundamental do Hidrogênio tem momento angular zero . Isso colocaria o elétron de Bohr no núcleo.
Bohr ajustou os dados, com algum elemento de verdade, mas seu modelo está ERRADO .
Derivações e Cálculos
Black Body Radiation Formulas *
Ainda não disponível
A constante de estrutura fina e o potencial de Coulomb
Vamos agora enfrentar pela primeira vez o problema de qual conjunto de unidades usar. Textos avançados normalmente usam unidades CGS em que a energia potencial é
enquanto as unidades internacionais padrão
Podemos contornar o problema definindo a constante de estrutura fina adimensional ![]() .
.
Portanto, em qualquer conjunto de unidades, o potencial de hidrogênio é
Exemplos
A Temperatura Solar
Estime a temperatura solar usando
- a intensidade da radiação solar na terra de 1,4 quilowatts por metro quadrado. ( m, m)
- e o espectro solar que atinge o pico a cerca de 500 nm.
Primeiro, calculamos a energia irradiada por unidade de área na superfície solar.
Comparamos isso com a expectativa em função da temperatura.
e pegue
Vamos supor que os 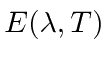 picos sejam de 500 nm, como mostra um dos gráficos. Precisamos nos transformar
picos sejam de 500 nm, como mostra um dos gráficos. Precisamos nos transformar 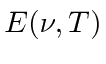 . Lembre-se de funções de distribuição.
. Lembre-se de funções de distribuição. 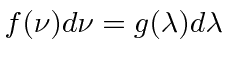
Este pico quando
é máximo.
Vamos definir 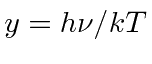 e resolver a equação
e resolver a equação
Resolvi isso iterativamente começando em y = 5 e comecei a  sugerir
sugerir
Isso concorda bem.
Radiação de corpo negro do universo inicial *
Encontre a frequência ![]() em que o Emissivo
em que o Emissivo 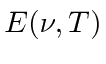 é máximo para a radiação cósmica de fundo de 2,7 graus. Encontre o comprimento
é máximo para a radiação cósmica de fundo de 2,7 graus. Encontre o comprimento ![]() de onda
de onda 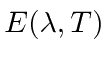 máximo.
máximo.
A radiação cósmica de fundo foi produzida quando o universo era muito mais quente do que agora. A maioria dos átomos do universo era ionizada e os fótons interagiam frequentemente com os íons ou elétrons livres. À medida que o universo esfriava, formando átomos neutros, os fótons se separavam da matéria e se propagavam pelo espaço. Hoje vemos esses fótons como a radiação de fundo. Como o universo está se expandindo, a radiação mudou para uma temperatura muito mais baixa do vermelho. Observamos cerca de 2,7 graus. A radiação de fundo é muito uniforme, mas estamos começando a observar não uniformidades no ![]() nível.
nível.
Do problema anterior, podemos dizer que o pico ![]() ocorre quando
ocorre quando
Da mesma forma, o pico ![]() ocorre quando
ocorre quando
Dispersão Compton *
Compton espalhou fótons de alta energia (essencialmente) de elétrons livres em 1923. Ele mediu o comprimento de onda dos fótons espalhados como uma função do ângulo de espalhamento. A figura abaixo mostra o estado inicial (a) e o estado final, com o fóton espalhado por um ângulo ![]() e o elétron recuando em um ângulo
e o elétron recuando em um ângulo ![]() . Os fótons eram provenientes do decaimento nuclear e, portanto, eram de energia alta o suficiente para que não importasse que os elétrons estivessem realmente ligados aos átomos. Queremos derivar a fórmula para o comprimento de onda do fóton espalhado em função do ângulo .
. Os fótons eram provenientes do decaimento nuclear e, portanto, eram de energia alta o suficiente para que não importasse que os elétrons estivessem realmente ligados aos átomos. Queremos derivar a fórmula para o comprimento de onda do fóton espalhado em função do ângulo .
Resolvemos o problema usando apenas a conservação de energia e momento. Vamos trabalhar em unidades em que ![]() por enquanto. Colocaremos as
por enquanto. Colocaremos as ![]() costas no final. Suponha que o fóton esteja inicialmente se movendo na
costas no final. Suponha que o fóton esteja inicialmente se movendo na ![]() direção com energia E e que ele se espalhe no
direção com energia E e que ele se espalhe no ![]() plano de forma que
plano de forma que 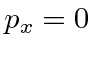 . A conservação do momento dá
. A conservação do momento dá
e
Conservação de energia dá
Nosso objetivo é resolver para ![]() em termos de,
em termos de, ![]() então vamos nos certificar de que eliminamos o
então vamos nos certificar de que eliminamos o ![]() . Continuando da equação de energia
. Continuando da equação de energia
quadratura e cálculo ![]() dos componentes
dos componentes
e escrever os quadrados do lado direito
e removendo coisas que aparecem em ambos os lados
e agrupamento
Já que em nossas unidades finas, 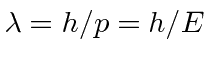
Agora aplicamos a velocidade da luz para fazer com que as unidades tenham um comprimento.
Esses cálculos podem ser bastante frustrantes se você não decidir quais variáveis deseja manter e quais deve eliminar de suas equações. Neste caso, eliminamos ![]() usando a equação de energia e computação
usando a equação de energia e computação ![]() .
.
Tamanho nuclear de Rutherford
Se a carga positiva nos átomos de ouro fosse uniformemente distribuída em uma esfera ou raio de 5 Angstroms, qual é a ![]() energia cinética máxima da partícula pela qual o
energia cinética máxima da partícula pela qual o ![]() pode ser espalhado de volta na direção de onde veio?
pode ser espalhado de volta na direção de onde veio?
Para resolver isso, precisamos calcular o potencial no centro da distribuição de carga em relação ao potencial no infinito (que diremos que é zero). Isso nos diz diretamente a energia cinética em eV necessária para arar através da distribuição de carga.
O potencial na superfície do núcleo é onde Z é o número de prótons no átomo e R é o raio nuclear. Essa é a parte fácil. Agora precisamos integrar nosso caminho para o centro. 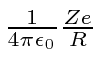
O dá a fração da carga nuclear dentro de um raio . ![]()
![]()
Então
Então, é a energia cinética em eV necessária para que uma partícula de carga ![]() atravesse o centro de uma distribuição esférica de carga. A
atravesse o centro de uma distribuição esférica de carga. A ![]() partícula realmente tem carga,
partícula realmente tem carga, 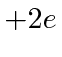 então precisamos multiplicar por 2. Para um raio nuclear de 5 Å ou metros, precisamos de cerca de 680 eV para arar através do núcleo. Para o raio nuclear real de cerca de 5 Fermis ou metros, precisamos de 68 MeV para arar.
então precisamos multiplicar por 2. Para um raio nuclear de 5 Å ou metros, precisamos de cerca de 680 eV para arar através do núcleo. Para o raio nuclear real de cerca de 5 Fermis ou metros, precisamos de 68 MeV para arar. 
Vamos comparar os números das unidades SI acima com meu método sugerido de usar a constante de estrutura fina ... Colocando a carga alfa de ![]() .
.
Isso é mais fácil.
Problemas de teste de amostra
- Qual é o comprimento de onda máximo da radiação eletromagnética que pode ejetar elétrons de um metal com função de trabalho de 3 eV? (3 pontos)
Resposta
A energia mínima do fóton necessária para eliminar um elétron é 3 eV. Só precisamos converter isso para comprimento de onda. - Com base no eletromagnetismo clássico e na mecânica estatística, Rayleigh calculou a densidade de energia dentro de uma cavidade. Ele descobriu que, a uma temperatura T, a densidade de energia em função da frequência era
Por que isso está relacionado à radiação do corpo negro? Por que isso estava em desacordo óbvio com a observação? - Qual é o comprimento de onda máximo da radiação eletromagnética que pode ejetar elétrons de um metal com função de trabalho de 2 eV?
- Diga simplesmente que problema com a radiação de corpo negro fez com que Plank propusesse a relação
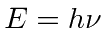 para a luz.
para a luz. - A função de trabalho de um metal é 2 eV. Suponha que um feixe de luz de comprimento de onda
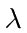 incida sobre uma superfície polida do metal. Trace a energia máxima do elétron (em eV) dos elétrons ejetados do metal
incida sobre uma superfície polida do metal. Trace a energia máxima do elétron (em eV) dos elétrons ejetados do metal 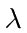 em relação aos Angstroms. Certifique-se de rotular ambos os eixos com alguns valores numéricos.
em relação aos Angstroms. Certifique-se de rotular ambos os eixos com alguns valores numéricos.
Para ondas EM , a intensidade e, portanto, a probabilidade de encontrar um fóton, é proporcional ao quadrado dos campos. Os campos obedecem à equação de onda. Os campos de duas fendas podem adicionar padrões de interferência de forma construtiva ou destrutiva. Os campos ![]() e
e ![]() estão 90 graus defasados e ambos contribuem para a intensidade.
estão 90 graus defasados e ambos contribuem para a intensidade.
Usaremos as mesmas idéias para elétrons , embora os detalhes do campo variem um pouco porque elétrons e fótons são tipos de partículas um tanto diferentes. Para ambas as partículas, o comprimento de onda é dado por
e a frequência por
Usaremos uma amplitude de probabilidade complexa 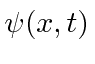 para o elétron. As partes reais e imaginárias estão defasadas como os campos EM. A onda progressiva com momentum
para o elétron. As partes reais e imaginárias estão defasadas como os campos EM. A onda progressiva com momentum ![]() e energia,
e energia, ![]() então, é
então, é
A probabilidade de encontrar um elétron é igual ao quadrado absoluto da amplitude de probabilidade complexa.
(Superaremos o problema de que essa probabilidade é 1 em todos os lugares para nossa função de onda simples.)
Acabamos de incluir a maior parte da física da Mecânica Quântica. Muito do que fizermos no restante do curso será deduzido do parágrafo acima. Nossa contribuição veio de deBroglie e Plank, com suporte de experimentos.
Vamos resumir a entrada da física novamente.
- Partículas livres são representadas por funções de onda complexas com uma relação entre suas propriedades de partícula - energia e momento, e suas propriedades de onda - frequência e comprimento de onda dados por Plank e deBroglie.
- O quadrado absoluto da função de onda fornece a função de distribuição de probabilidade. A mecânica quântica apenas nos diz a probabilidade.
- Podemos fazer sobreposições de nossas funções de onda de partículas livres para criar estados que não têm momento definido. Veremos que qualquer estado pode ser feito a partir da superposição de estados de partículas livres com diferentes momentos.
Agora temos uma dualidade onda-partícula para todas as partículas; no entanto, a física agora apenas nos diz a probabilidade de ocorrerem alguns eventos quânticos. Perdemos o poder preditivo completo da física clássica.
Gasiorowicz Capítulo 1
Rohlf Capítulo 5
Griffiths 1.2, 1.3
Cohen-Tannoudji et al. Capítulo
Derivações e cálculos
Revisão de números complexos
Esta é uma revisão simples, mas você deve certificar-se de usar números complexos corretamente. Um dos erros mais comuns em problemas de teste é esquecer de usar o conjugado complexo ao calcular uma probabilidade.
Um número complexo 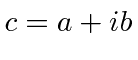 consiste em uma parte real
consiste em uma parte real ![]() e uma parte imaginária
e uma parte imaginária ![]() . (Escolhemos
. (Escolhemos ![]() e
e ![]() para ser números reais.)
para ser números reais.) ![]() É a raiz quadrada de -1.
É a raiz quadrada de -1.
O conjugado complexo de ![]() é
é 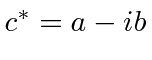 . (Basta mudar o sinal de todos os
. (Basta mudar o sinal de todos os ![]() .)
.)
O quadrado absoluto de um número complexo é calculado multiplicando-o por seu conjugado complexo.
Isso dá a magnitude ao quadrado do número complexo. O quadrado absoluto é sempre real.
Usaremos exponenciais complexas o tempo todo.
Você pode verificar se o quadrado absoluto dessas exponenciais é sempre 1. Elas costumam ser chamadas de fator de fase.
Como acontece com outros exponenciais, podemos multiplicá-los adicionando os expoentes.
Revisão das Ondas Viajantes
Uma onda viajante normal pode ser dada por
A fase da onda passa ![]() em um comprimento de onda em
em um comprimento de onda em ![]() . Portanto, o comprimento de onda
. Portanto, o comprimento de onda ![]() satisfaz
satisfaz
Da mesma forma, a fase passa ![]() em um período
em um período ![]() de tempo.
de tempo.
![]() é a frequência angular. Ele muda a
é a frequência angular. Ele muda a ![]() cada ciclo. A frequência
cada ciclo. A frequência ![]() aumenta em 1 a cada ciclo, então
aumenta em 1 a cada ciclo, então
Não há razão para memorizar essas equações. Eles devem ser óbvios.
Vamos ver o quão rápido um dos picos da onda se move. Isso é chamado de velocidade de fase. No momento ![]() , há um pico em
, há um pico em ![]() . Este é o pico para o qual o argumento do cosseno é 0. No momento
. Este é o pico para o qual o argumento do cosseno é 0. No momento ![]() , o argumento é zero quando
, o argumento é zero quando ![]() ou em . Se calcularmos a velocidade de fase tomando , obtemos
ou em . Se calcularmos a velocidade de fase tomando , obtemos 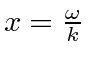
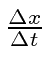
Ou seja, um dos picos dessa onda viaja com velocidade de
Em QM não-relativista, temos 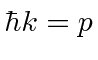 ,
, ![]() e , por isso,
e , por isso, 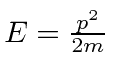
Você deve se lembrar que um pulso se moverá na velocidade do grupo que é dada por
(A velocidade de fase para o caso não relativístico é .)
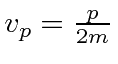
Problemas de teste de amostra
- Escreva as duas funções de onda de partícula livre (não normalizadas) para uma partícula de energia cinética E. Inclua a dependência de tempo adequada e expressões para outras constantes em termos de E.
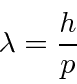
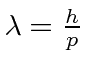
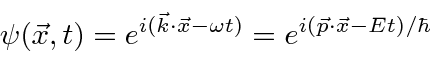
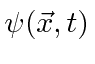
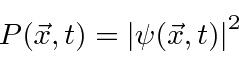
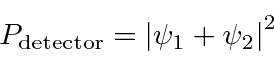
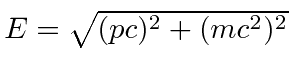
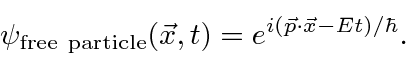
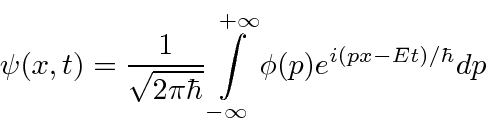
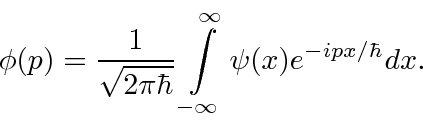
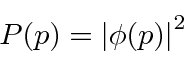
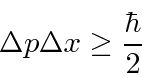
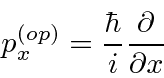
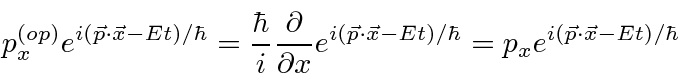
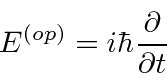
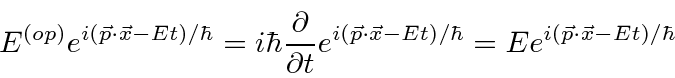
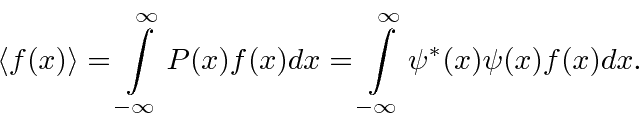
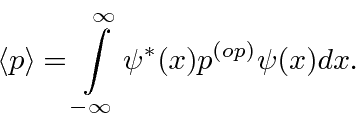
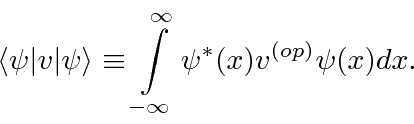
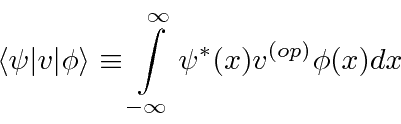
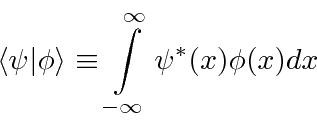
![\ begin {displaymath} \ bgroup \ color {black} [p, x] \ equiv px-xp = {\ hbar \ over i}. \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img82.png)
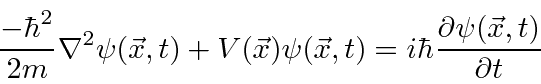
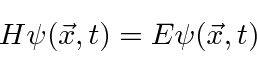
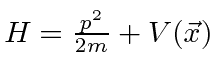
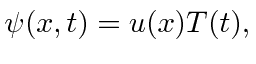
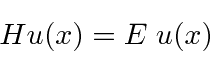
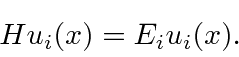
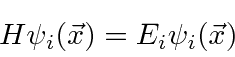
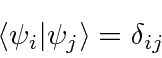
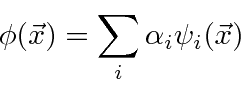
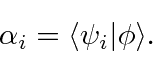
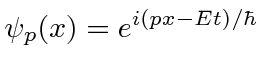
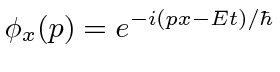
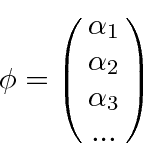
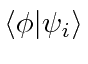
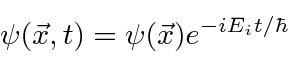
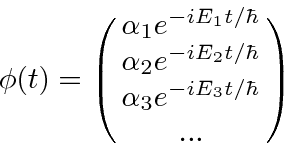
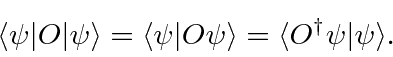
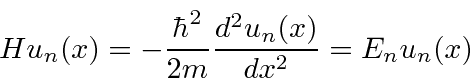
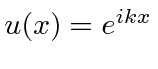
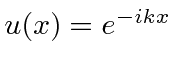
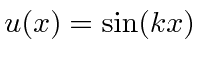
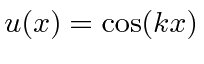
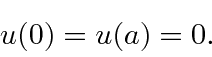
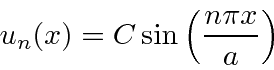
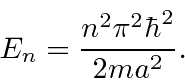
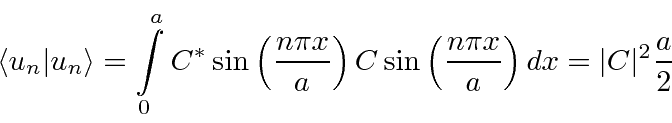
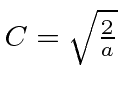
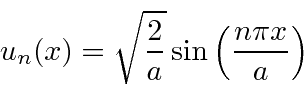
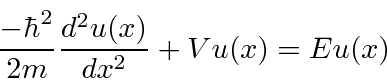
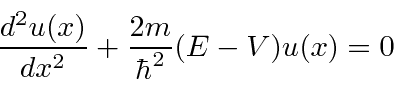
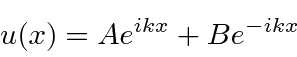
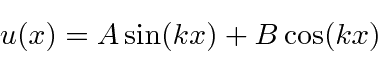
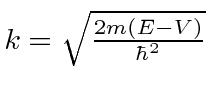
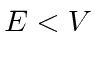

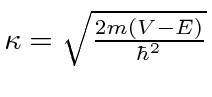
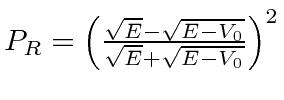
![\ bgroup \ color {black} $ j = {\ hbar \ over 2im} [u ^ * {du \ over dx} - {du ^ * \ over dx} u] $ \ egroup](https://quantummechanics.ucsd.edu/ph130a/130_notes/img146.png)
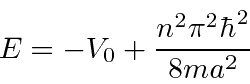
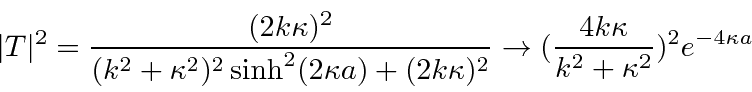
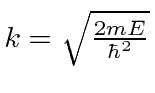
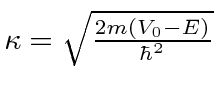
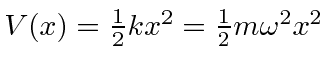
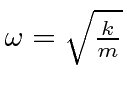
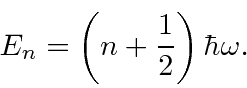
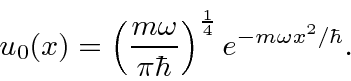
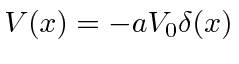
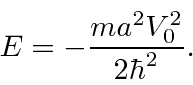
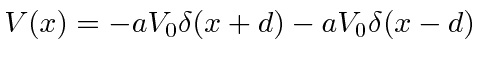
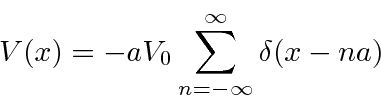
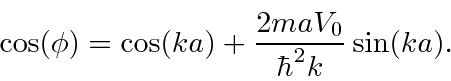
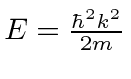
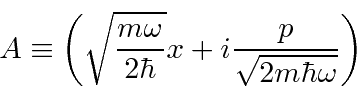
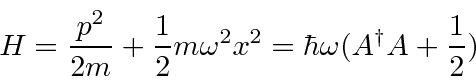
![\ begin {displaymath} \ bgroup \ color {black} [A, A ^ \ dagger] = {i \ over 2 \ hbar} (- [x, p] + [p, x]) = 1 \ egroup \ end { displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img179.png)
![\ begin {displaymath} \ bgroup \ color {black} [H, A] = \ hbar \ omega [A ^ \ dagger A, A] = \ hbar \ omega [A ^ \ dagger, A] A = - \ hbar \ omega A \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img180.png)
![\ begin {displaymath} \ bgroup \ color {black} [H, A ^ \ dagger] = \ hbar \ omega [A ^ \ dagger A, A ^ \ ... ... \ hbar \ omega A ^ \ dagger [ A, A ^ \ dagger] = \ hbar \ omega A ^ \ dagger \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img181.png)
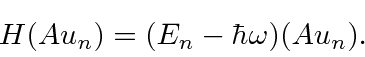
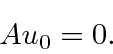
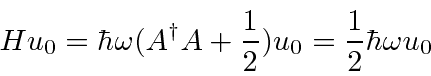
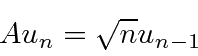
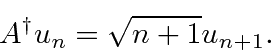
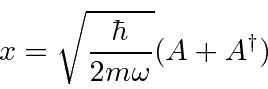
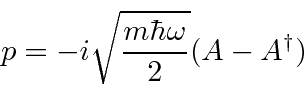
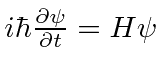
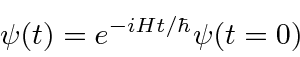
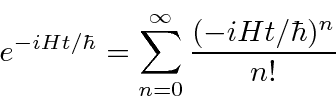
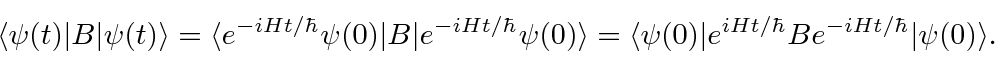
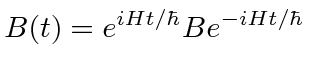
![\ begin {displaymath} \ bgroup \ color {black} (\ Delta A) (\ Delta B) \ geq {i \ over 2} \ langle [A, B] \ rangle \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img205.png)
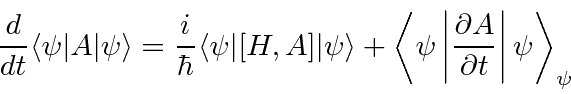
![\ begin {displaymath} \ bgroup \ color {black} {d \ langle x \ rangle \ over dt} = {i \ over \ hbar} ... ... 2 \ over 2m}, x] \ rangle = \ left \ langle {p \ over m} \ right \ rangle \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img207.png)
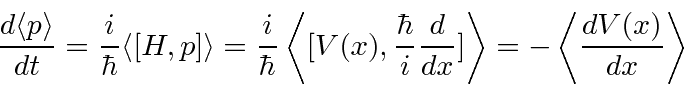
![\ begin {displaymath} \ bgroup \ color {black} [p _ {(2) z}, z _ {(2)}] = {\ hbar \ over i} \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img209.png)
![\ begin {displaymath} \ bgroup \ color {black} [p _ {(1) x}, x _ {(2)}] = [p _ {(2) z}, y _ {(2)}] = 0. \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img210.png)
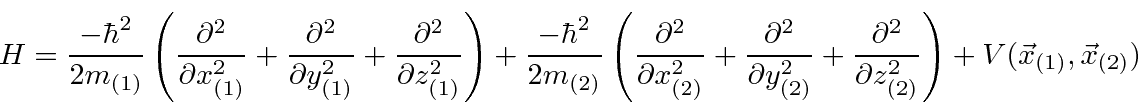
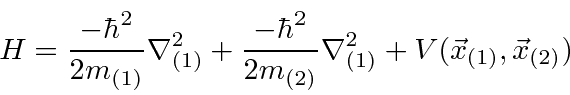
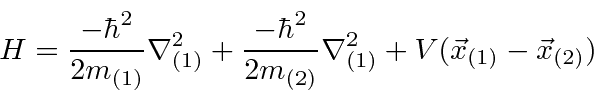
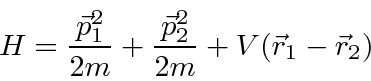
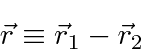
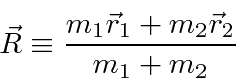
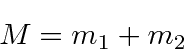
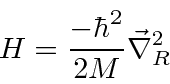
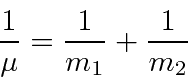
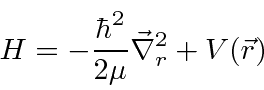
![\ begin {displaymath} \ bgroup \ color {black} [H, P_ {12}] = 0 \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img224.png)
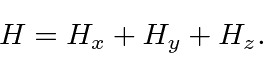
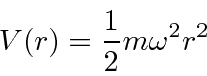
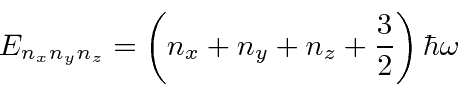
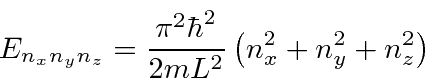
![\ begin {displaymath} \ bgroup \ color {black} [H, L_z] = [H, L_x] = [H, L_y] = 0 \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img234.png)
![\ begin {displaymath} \ bgroup \ color {black} [L_x, L_y] \ neq 0 \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img235.png)
![\ begin {displaymath} \ bgroup \ color {black} [L ^ 2, L_z] = 0 \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img237.png)
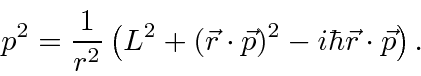
![\ begin {displaymath} \ bgroup \ color {black} {- \ hbar ^ 2 \ over 2 \ mu} \ left [{1 \ over r ^ 2} \ le ... ... r ^ 2} \ right] u_E (\ vec {r}) + V (r) u_E (\ vec {r}) = Eu_E (\ vec {r}) \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img242.png)
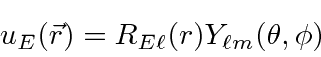
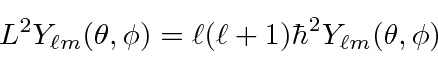
![\ begin {displaymath} \ bgroup \ color {black} {- \ hbar ^ 2 \ over 2 \ mu} \ left [{1 \ over r ^ 2} \ le ... ... r ^ 2} \ right] R_ {E \ ell} (r) + V (r) R_ {E \ ell} (r) = ER_ {E \ ell} (r) \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img246.png)
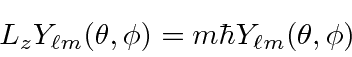
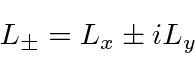
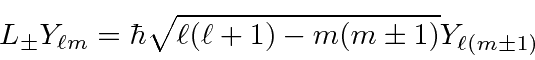
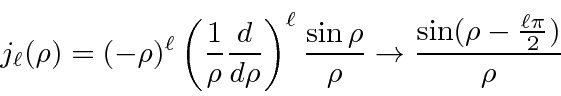
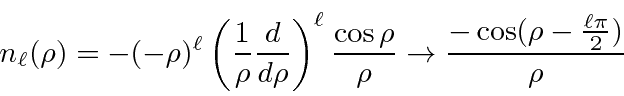
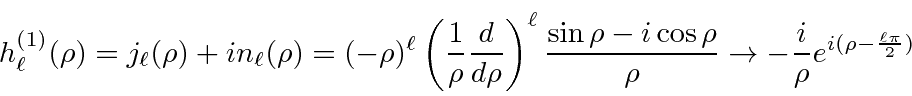
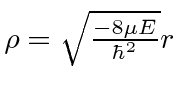
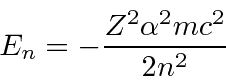
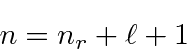
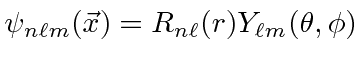
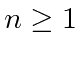
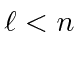
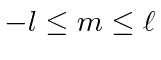
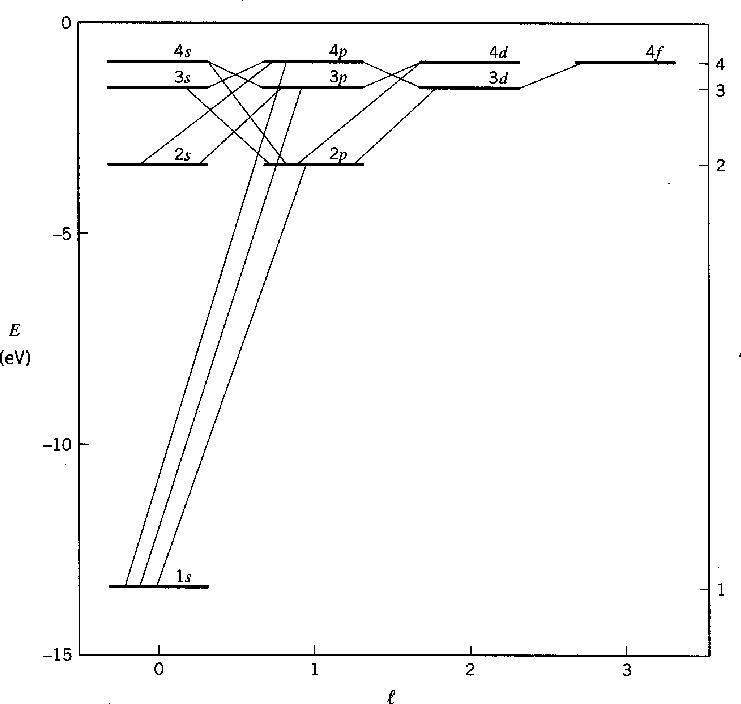
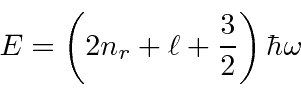
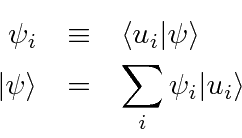
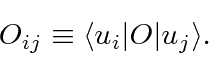

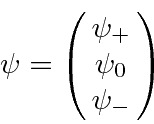
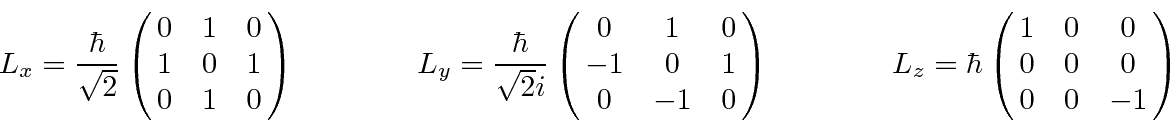
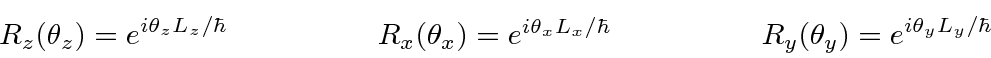
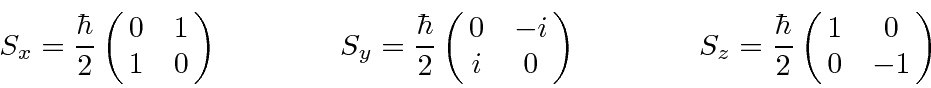
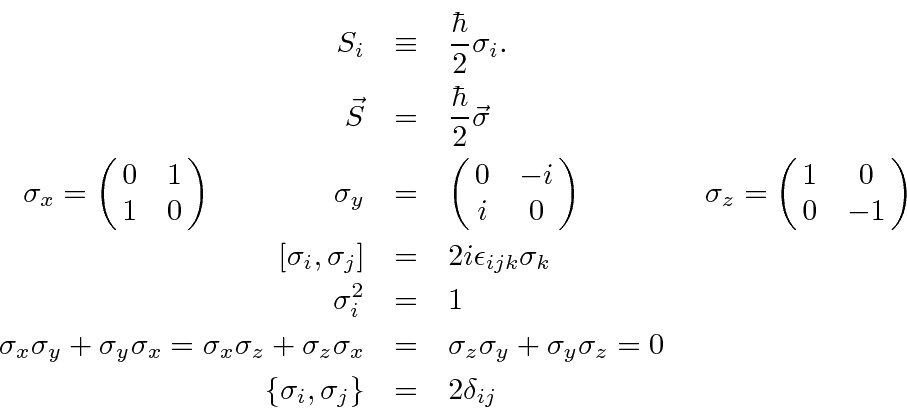
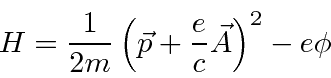
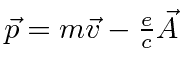
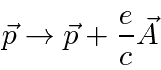
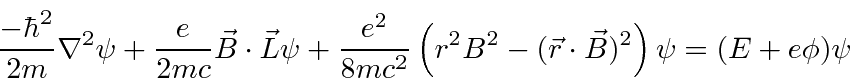
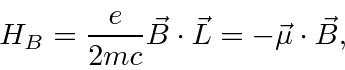
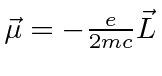
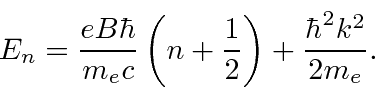
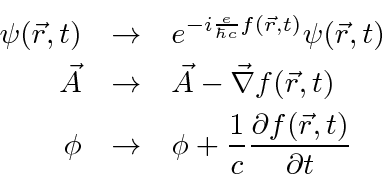
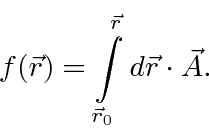
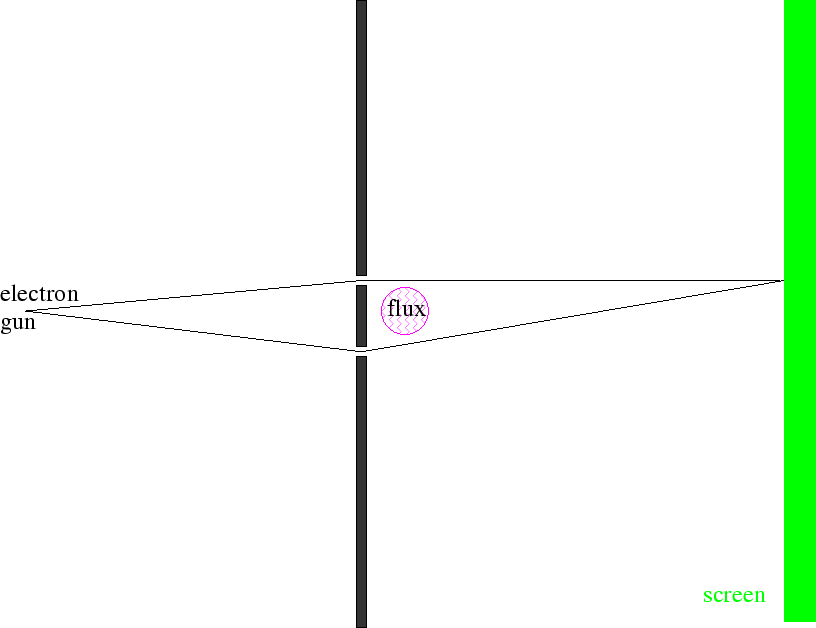
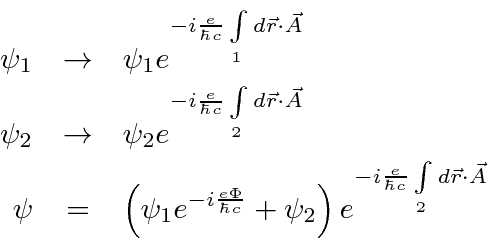
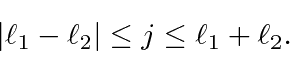
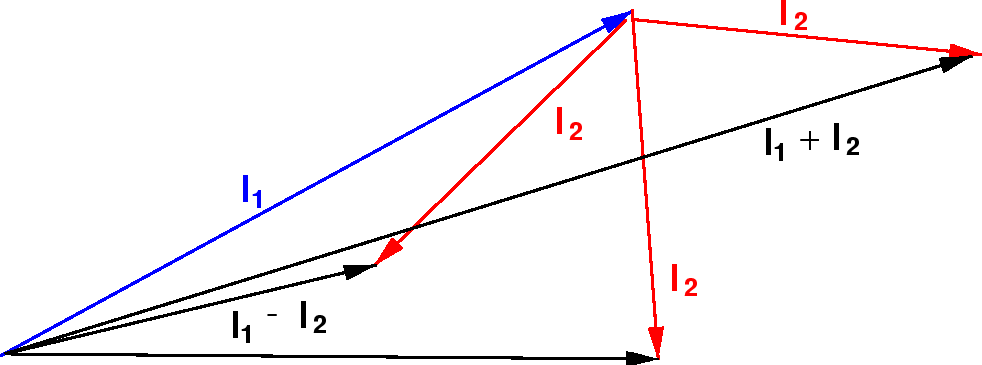
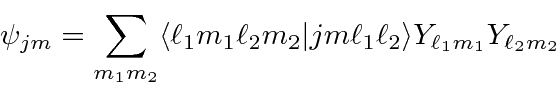
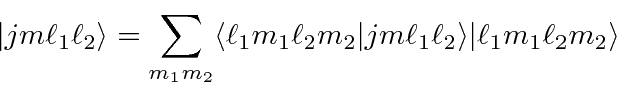
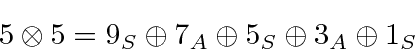
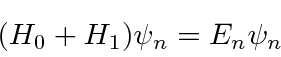
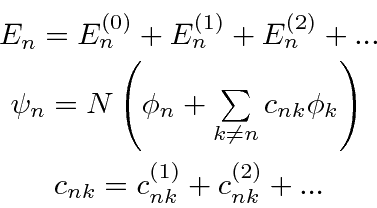
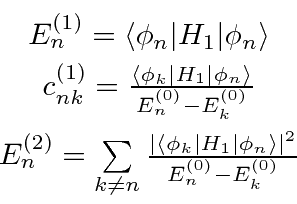
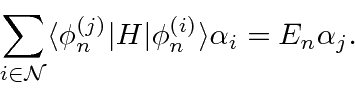
![\ begin {displaymath} \ bgroup \ color {black} E_ {nlm} = E ^ {(0)} _ n + {{E ^ {(0)} _ n} ^ 2 \ over {2mc ^ 2}} \ left [ 3 - {4n \ over {j + {1 \ over 2}}} \ right] \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img327.png)
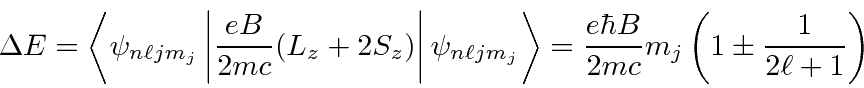
![\ begin {displaymath} \ bgroup \ color {black} E_ {njm_j \ ell s} = - {1 \ over 2} \ alpha ^ 2mc ^ 2 \ ... ... er j + {1 \ over 2}} - {3 \ over 4n} \ right] \ right) + g_L \ mu_BBm_j \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img331.png)
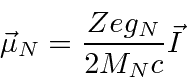
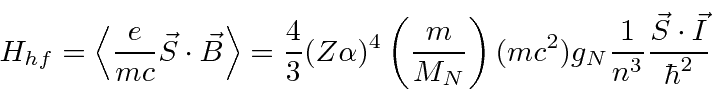
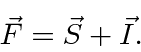
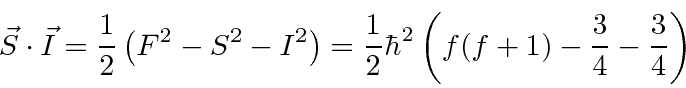
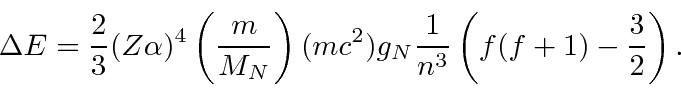
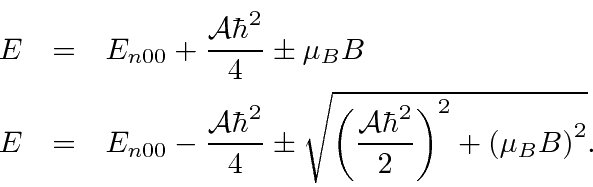
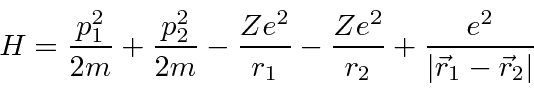
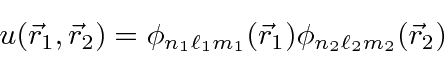
![\ begin {displaymath} \ bgroup \ color {black} \ left [\ sum \ limits ^ Z_ {i = 1} \ left ({p ^ 2_i \ o ... ... \ vert \ vec {r_i} - \ vec {r_j} \ right \ vert}} \ right] \ psi = E \ psi. \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img361.png)
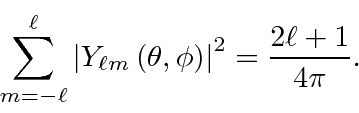
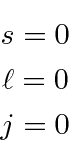
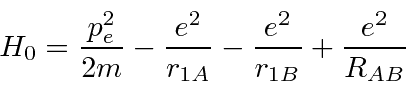
![\ begin {displaymath} \ bgroup \ color {black} \ psi_ \ pm \ left (\ vec {r}, \ vec {R} \ right) = C_ \ pm (R) \ left [\ psi_A \ pm \ psi_B \ direita] \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img370.png)
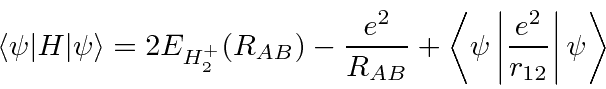
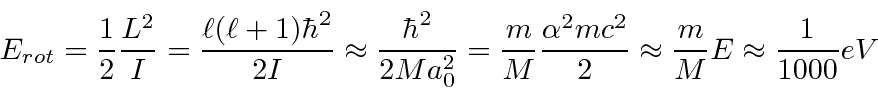
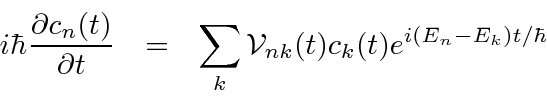
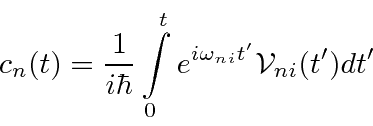
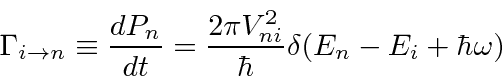
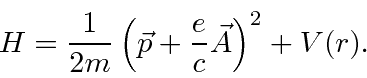
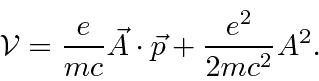
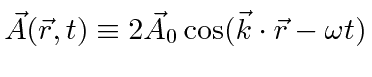
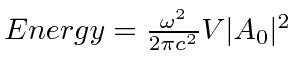
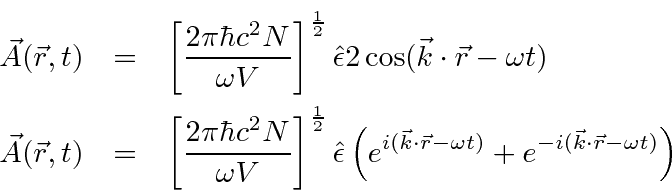
![\ begin {eqnarray *} \ vec {A} (\ vec {r}, t) & = & \ left [{2 \ pi \ hbar c ^ 2 \ over \ omega V} \ right] ... ... \ omega t)} + \ sqrt {N + 1} e ^ {- i (\ vec {k} \ cdot \ vec {r} - \ omega t)} \ right) \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img398.png)
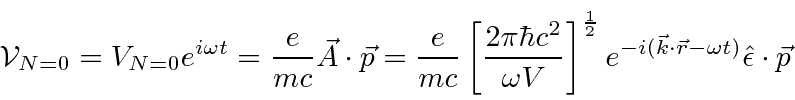
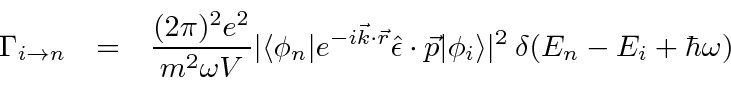
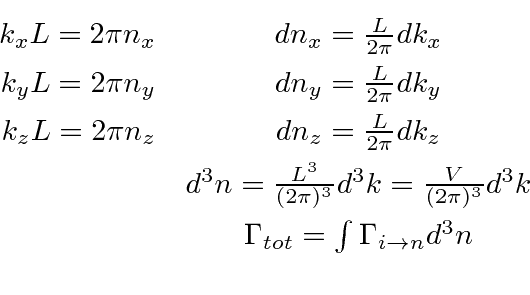
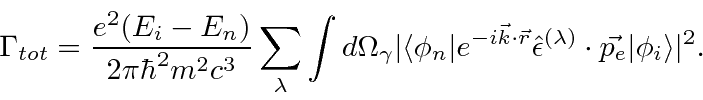
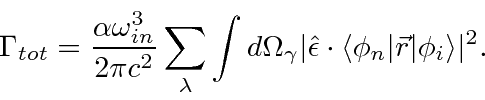
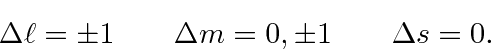
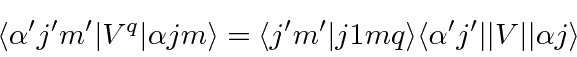
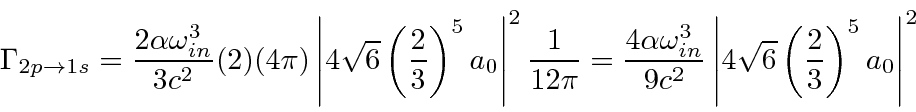
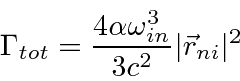
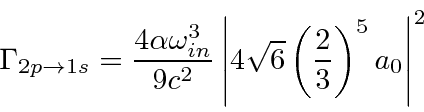
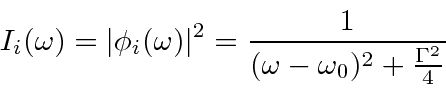
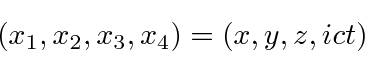
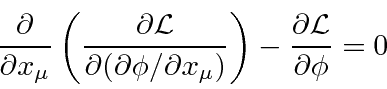
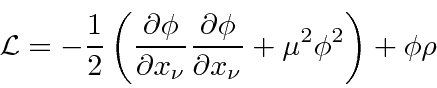
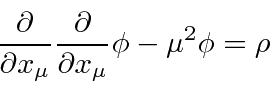
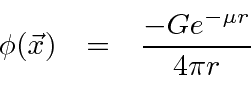
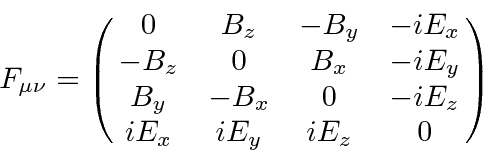
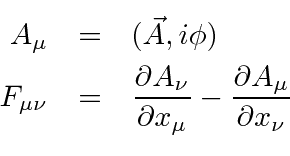
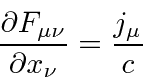
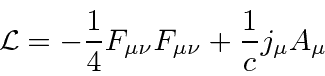
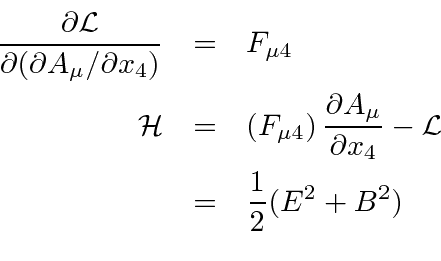
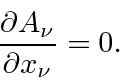
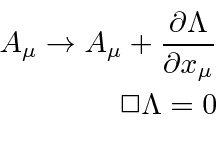
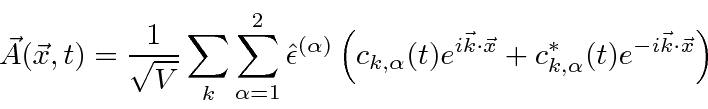
![\ begin {eqnarray *} H & = & \ sum \ limits_ {k, \ alpha} \ left ({\ omega \ over c} \ right) ^ 2 \ left ... ... (t) c_ {k, \ alpha} ^ * (t) + c_ {k, \ alpha} ^ * (t) c_ {k, \ alpha} (t) \ right] \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img441.png)
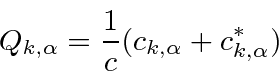
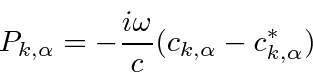
![\ begin {eqnarray *} \ left [Q_ {k, \ alpha}, P_ {k ', \ alpha'} \ right] & = & i \ hbar \ delta_ {kk '} \ ... ... \ right] & = & 0 \\ \ left [P_ {k, \ alpha}, P_ {k ', \ alpha'} \ right] & = & 0 \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img444.png)
![\ begin {eqnarray *} a_ {k, \ alpha} & = & {1 \ over \ sqrt {2 \ hbar \ omega}} (\ omega Q_ {k, \ alpha} ... ... \ alpha '} ^ \ dagger \ right] & = & \ delta_ {kk '} \ delta _ {\ alpha \ alpha'} \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img445.png)
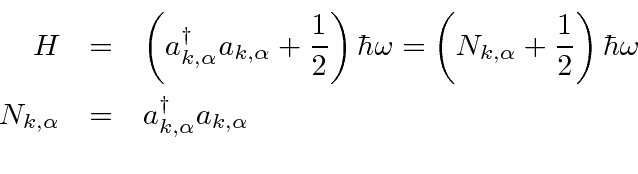

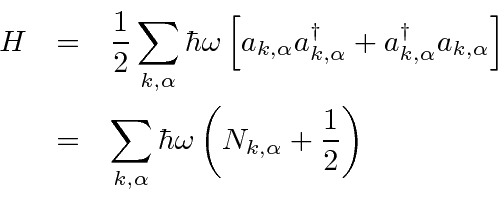
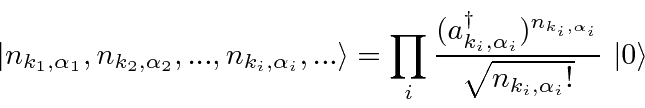
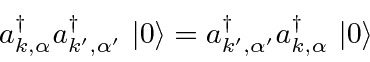
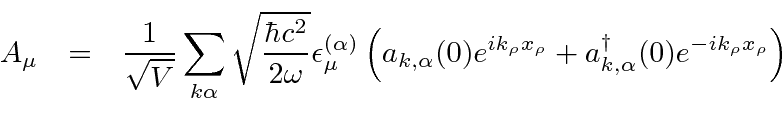
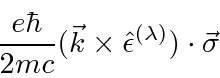
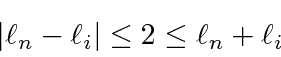
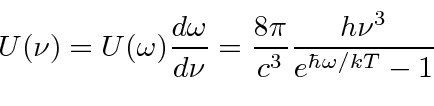
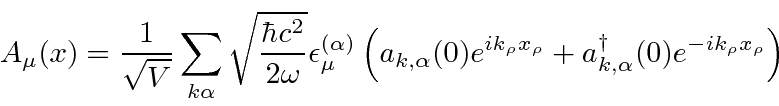
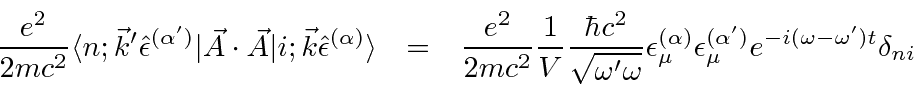
![\ begin {displaymath} \ bgroup \ color {black} {d \ sigma \ over d \ Omega} = \ left ({e ^ 2 \ over ... ... ângulo \ over \ omega_ {ji} + \ omega ' } \ right] \ right \ vert ^ 2 \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img464.png)
![\ begin {displaymath} \ bgroup \ color {black} {d \ sigma_ {elas} \ over d \ Omega} = \ left ({e ^ ... ... rangle \ over \ omega_ {ji} + \ omega} \ right] \ right \ vert ^ 2 \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img465.png)
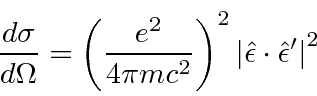
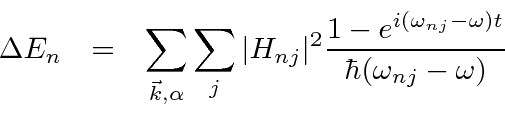
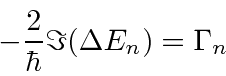
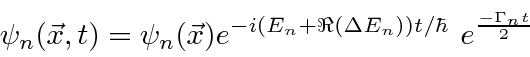
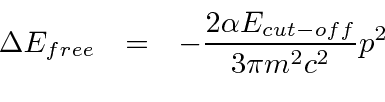
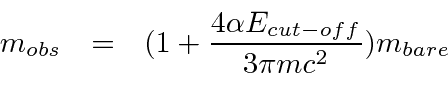
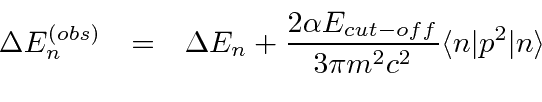
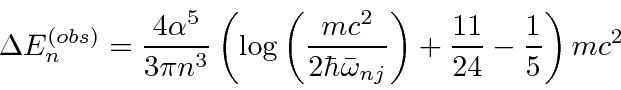
![\ begin {displaymath} \ bgroup \ color {black} H = {1 \ over 2m} \ left (\ vec {\ sigma} \ cdot [\ ve ... ... {e \ over c} \ vec {A } (\ vec {r}, t)] \ right) ^ 2-e \ phi (\ vec {r}, t) \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img482.png)
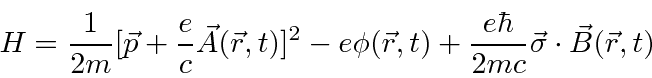
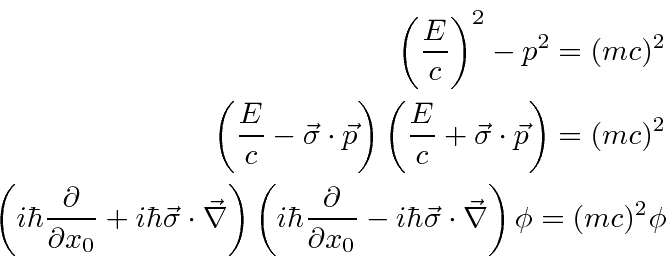
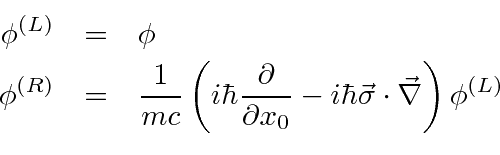
![\ begin {eqnarray *} \ pmatrix {-i \ hbar {\ partial \ over \ partial x_0} & -i \ hbar \ vec {\ sig ... ...] = \ hbar \ left [\ gamma_ \ mu { \ partial \ over \ partial x_ \ mu} \ right] \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img489.png)
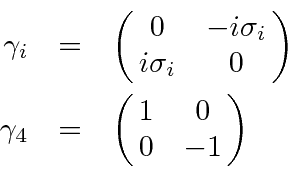
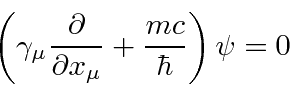
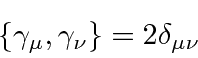
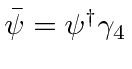
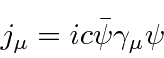
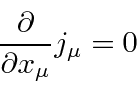
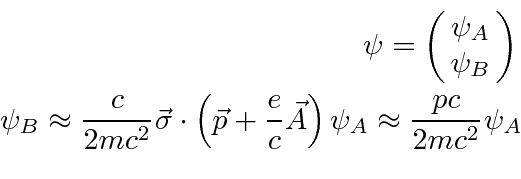
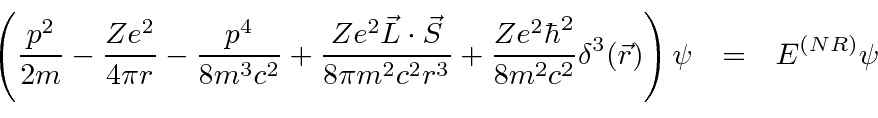
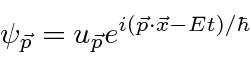
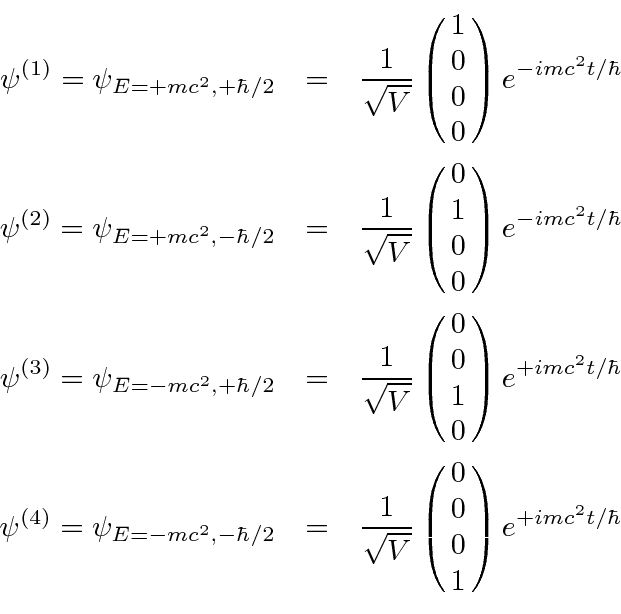
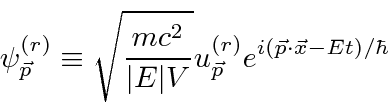
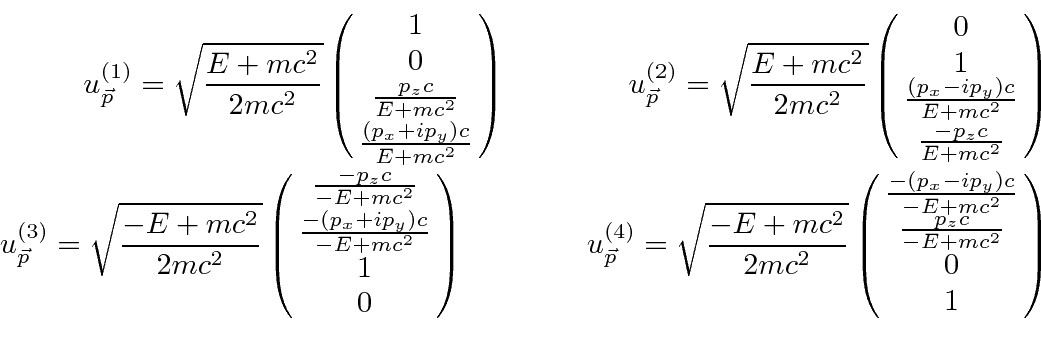
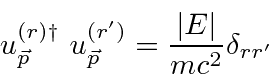
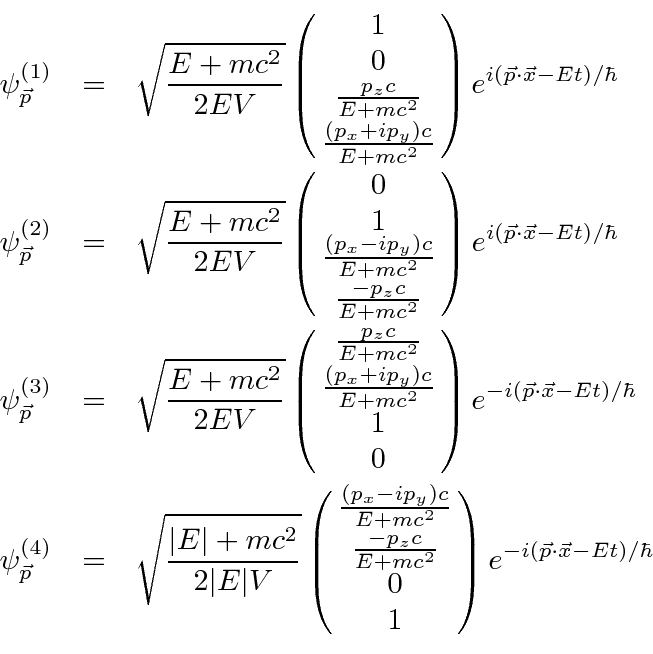
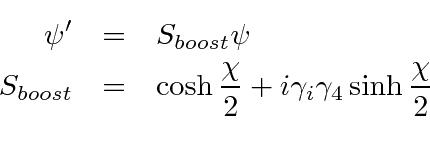
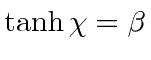
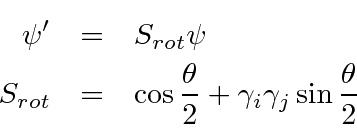
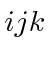
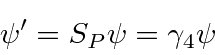
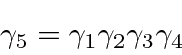
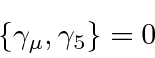
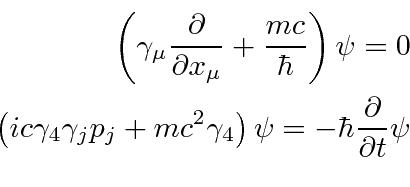
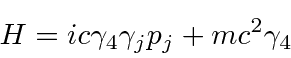
![\ begin {displaymath} \ bgroup \ color {black} [H, L_z] = ic \ gamma_4 [\ gamma_jp_j, xp_y-yp_x] = \ hbar c \ gamma_4 (\ gamma_1p_y- \ gamma_2 p_x) \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img539.png)
![\ begin {displaymath} \ bgroup \ color {black} {[H, S_z]} = \ hbar c \ gamma_4 [\ gamma_2p_x- \ gamma_1p_y] \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img540.png)
![\ begin {eqnarray *} [H, J_z] = [H, L_z] + [H, S_z] = \ hbar c \ gamma_4 (\ gamma_1p_y- \ gamma_2 p_x) + \ hbar c \ gamma_4 [\ gamma_2p_x- \ gamma_1p_y] = 0 \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img541.png)
![\ begin {displaymath} \ bgroup \ color {black} [H, \ vec {S} \ cdot \ vec {p}] = [H, \ vec {S}] \ cdot \ vec {p} = 0 \ egroup \ fim {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img542.png)
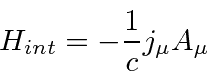
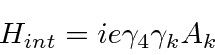
![\ begin {eqnarray *} \ langle v_k \ rangle & = & \ sum \ limits _ {\ vec {p}} \ sum \ limits_ {r = 1} ^ 4 \ ... ... mma_k u ^ {(r ') } _ {\ vec {p}} e ^ {2i \ vert E \ vert t / \ hbar} \ right] \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img546.png)