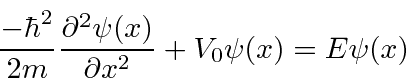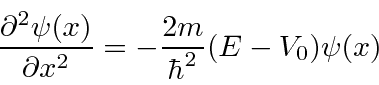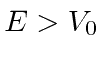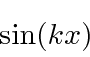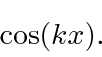Schrödinger desenvolveu uma equação diferencial para o desenvolvimento de uma função de onda no tempo . Como o operador Energia tem uma derivada de tempo, o operador de energia cinética tem derivadas de espaço, e esperamos que as soluções sejam ondas viajantes, é natural tentar uma equação de energia. A equação de Schrödinger é a declaração do operador de que a energia cinética mais a energia potencial é igual à energia total .
Derivando a equação dos operadores
Para uma partícula livre , temos
Vamos tentar esta equação em nossos estados de momentum definido .
A constante na frente da função de onda pode ser removida de ambos os lados. Está lá para normalização, não faz parte da solução. Vamos em frente e faremos a diferenciação.
Nossa função de onda será uma solução da equação de Schrödinger de partícula livre fornecida . Isso é exatamente o que queríamos. Portanto, construímos uma equação que tem as funções de onda esperadas como soluções. É uma equação de onda baseada na energia total.
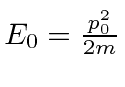
Adicionando energia potencial, temos a Equação de Schrödinger
ou
Onde
é o operador hamiltoniano.
Em três dimensões , isso se torna.
Nós o usaremos para resolver muitos problemas neste curso.Portanto, a Equação de Schrödinger é, em certo sentido, simplesmente a afirmação (nos operadores) de que a energia cinética mais a energia potencial é igual à energia total.
O Fluxo de Probabilidade *
Em analogia ao vetor de Poynting para radiação EM, podemos querer saber a probabilidade de corrente em alguma situação física. Por exemplo, em nossa solução de partículas livres, a densidade de probabilidade é uniforme em todo o espaço, mas há um fluxo líquido ao longo da direção do momento.
Podemos derivar uma equação que mostra a conservação da probabilidade diferenciando e usando a Equação de Schrödinger. 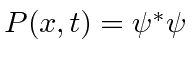
Esta é a equação de conservação usual se 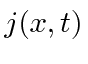 for identificada como a corrente de probabilidade.
for identificada como a corrente de probabilidade.
Esta corrente pode ser calculada a partir da função de onda.
Se integrarmos se ao longo de algum intervalo em ![]()
a equação diz que a taxa de mudança de probabilidade em um intervalo é igual ao fluxo de probabilidade para a integral menos o fluxo de saída.
Estendendo esta análise para 3 dimensões ,
com
A Equação de Onda de Schrödinger
A equação normal que obtemos, para ondas em uma corda ou na água, relaciona a derivada do segundo espaço com a derivada do segundo tempo. A equação de Schrödinger usa apenas a derivada da primeira vez , no entanto, a adição de ![]() relaciona a parte real da função de onda à parte imaginária, na verdade deslocando a fase em 90 graus como faria a 2ª derivada.
relaciona a parte real da função de onda à parte imaginária, na verdade deslocando a fase em 90 graus como faria a 2ª derivada.
A equação de Schrödinger é construída para funções de onda complexas .
Quando Dirac tentou fazer uma versão relativística da equação, onde a relação de energia é um pouco mais complicada, ele descobriu uma nova física.
Gasiorowicz Capítulo 3
Griffiths Capítulo 1
Cohen-Tannoudji et al. Capítulo
A equação de Schrödinger independente do tempo
Equações diferenciais de segunda ordem, como a Equação de Schrödinger, podem ser resolvidas por separação de variáveis . Essas soluções separadas podem então ser usadas para resolver o problema em geral.
Suponha que possamos fatorar a solução entre o tempo e o espaço.
Conecte isso à equação de Schrödinger.
Coloque tudo que depende
Uma vez que temos uma função de apenas
que tem uma solução geral simples ,
e uma equação em
que depende do problema a ser resolvido (por meio
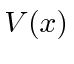 ).
).
A ![]() equação é freqüentemente chamada de Equação de Schrödinger independente do tempo .
equação é freqüentemente chamada de Equação de Schrödinger independente do tempo .
* Exemplo: Resolva a equação de Schrödinger para um potencial constante ![]() . *
. *
Derivações e cálculos
Operadores lineares
Operadores lineares ![]() satisfazem a equação
satisfazem a equação
Um exemplo de operador não linear (que não usaremos) é ![]() aquele que tem a propriedade
aquele que tem a propriedade
Equação de conservação de probabilidade
Comece pela probabilidade e diferencie com relação ao tempo.
Use a equação de Schrödinger
e seu conjugado complexo
(Presumimos que
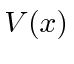 seja real. Potenciais imaginários fazem com que a probabilidade não seja conservada.)
seja real. Potenciais imaginários fazem com que a probabilidade não seja conservada.)
Agora precisamos conectar essas equações.
Esta é a equação de conservação usual se 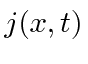 for identificada como a corrente de probabilidade.
for identificada como a corrente de probabilidade.
Exemplos
Solução para a equação de Schrödinger em um potencial constante
Suponha que queremos resolver a equação de Schrödinger em uma região na qual o potencial é constante e igual a ![]() . Encontraremos duas soluções para cada energia
. Encontraremos duas soluções para cada energia ![]() .
.
Temos a equação.
Lembre-se de que ![]() é uma variável independente na equação acima, enquanto
é uma variável independente na equação acima, enquanto ![]() e
e ![]() são constantes a serem determinadas na solução.
são constantes a serem determinadas na solução.
e
se definirmos ![]() pela equação . Estas são ondas viajando em direções opostas com a mesma energia (e magnitude do momento).
pela equação . Estas são ondas viajando em direções opostas com a mesma energia (e magnitude do momento). 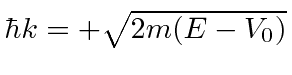
Também podemos usar as combinações lineares das duas soluções acima
e
Existem apenas duas soluções linearmente independentes. Precisamos escolher as funções exponenciais ou trigonométricas, não ambas. As soluções de sen e cos representam estados de energia definida, mas contêm partículas que se movem para a esquerda e para a direita. Eles não são estados de momentum definidos. Eles serão úteis para nós para algumas soluções.
As soluções também são tecnicamente corretas, 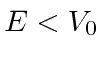 mas
mas ![]() se tornam imaginárias. Vamos escrever as soluções em termos de As soluções são
se tornam imaginárias. Vamos escrever as soluções em termos de As soluções são 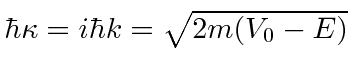
e
Não são ondas, mas exponenciais reais. Observe que essas são soluções para regiões onde a partícula não é permitida classicamente, devido à conservação de energia; a energia total é menor do que a energia potencial. Usaremos essas soluções em Mecânica Quântica.

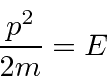
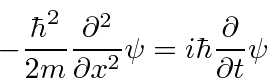
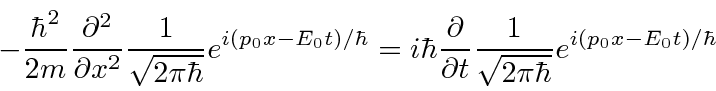
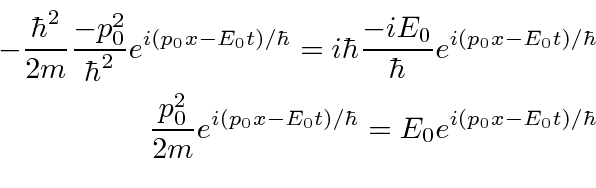
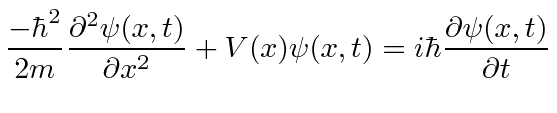
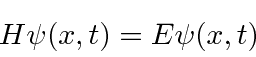
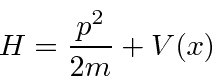
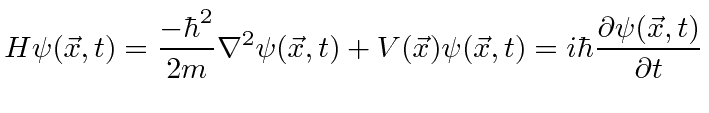
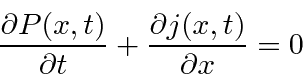
![\ begin {displaymath} \ bgroup \ color {black} j (x, t) = {\ hbar \ over 2mi} \ left [\ psi ^ * {\ pa ... ... r \ partial x} - {\ parcial \ psi ^ * \ over \ partial x} \ psi \ right] \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1065.png)
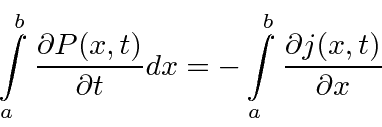
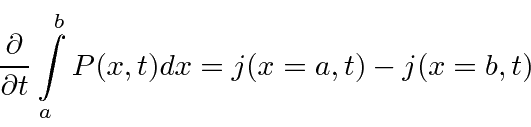
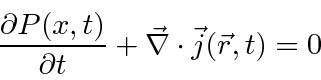
![\ bgroup \ color {black} $ \ displaystyle \ vec {j} (\ vec {r}, t) = {\ hbar \ over 2mi} \ left [\ ps ... ... bla} \ psi (\ vec {r}, t) - \ psi (\ vec {r}, t) \ vec {\ nabla} \ psi ^ * (\ vec {r}, t) \ right] $ \ egroup](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1069.png)
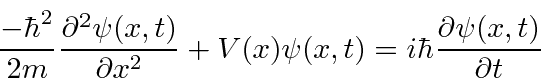
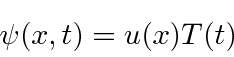
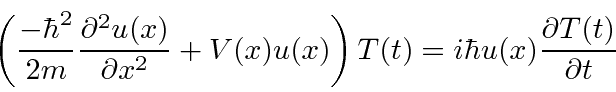
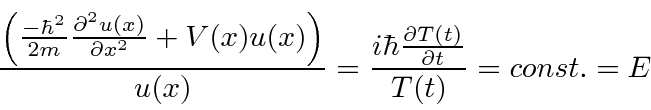
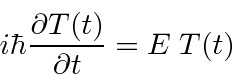
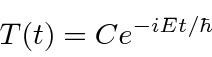
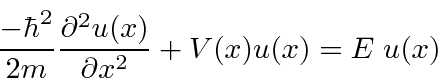
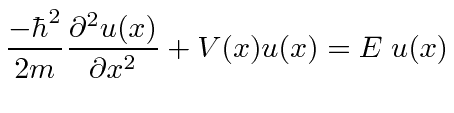
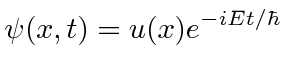
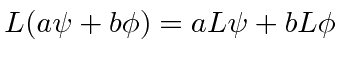
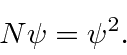
![\ begin {displaymath} \ bgroup \ color {black} {\ partial P (x, t) \ over \ partial t} = {\ parti ... ... rtial t} \ psi- \ psi ^ * {\ partial \ psi \ over \ partial t} \ right] \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1081.png)
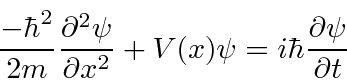
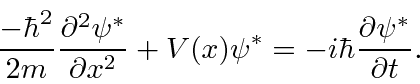
![\ begin {displaymath} \ bgroup \ color {black} {\ partial P (x, t) \ over \ partial t} = {1 \ over ... ... {\ partial ^ 2 \ psi \ over \ partial x ^ 2} + V (x) \ psi ^ * \ psi \ right] \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1084.png)
![\ begin {displaymath} \ bgroup \ color {black} = {1 \ over i \ hbar} {\ hbar ^ 2 \ over 2m} \ left [... ... tial x} \ psi- \ psi ^ * { \ partial \ psi \ over \ partial x} \ right] \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1085.png)