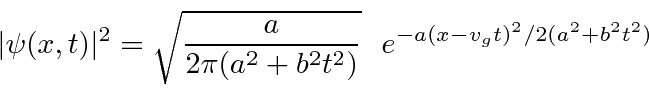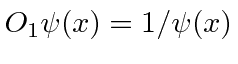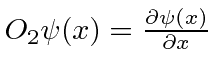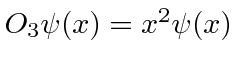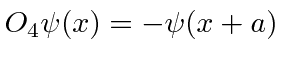Os operadores serão usados para nos ajudar a derivar uma equação diferencial que nossas funções de onda devem satisfazer. Eles também serão usados em quase todos os cálculos da Física Quântica.
Um exemplo de um operador linear é um operador diferencial simples como , o qual entendemos diferenciar tudo à direita dele com respeito a ![]() .
.![]()
Operadores no espaço de posição
Para encontrar operadores para variáveis físicas no espaço de posição, examinaremos as funções de onda com momento definido. Nosso estado de momentum definido ![]() (e energia definida
(e energia definida ![]() ) é
) é
Podemos construir qualquer outro estado a partir da superposição desses estados usando a transformada de Fourier.
O Operador Momentum
Determinamos o operador de momentum exigindo que, quando operamos com 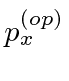 on
on 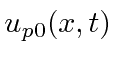 , obtemos
, obtemos ![]() vezes a mesma função de onda.
vezes a mesma função de onda.
Isso significa que, para esses estados de momentum definidos, multiplicar por 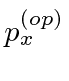 é o mesmo que multiplicar pela variável
é o mesmo que multiplicar pela variável ![]() . Descobrimos que isso é verdade para o seguinte operador de momento .
. Descobrimos que isso é verdade para o seguinte operador de momento .
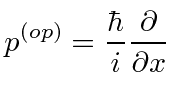 |
Podemos verificar que isso funciona por cálculo explícito.
Se pegarmos nosso operador de momentum e agirmos em um estado arbitrário ,
ele nos dá o direito ![]() para cada termo na integral. Isso nos permitirá calcular os valores esperados para qualquer variável que possamos representar por um operador.
para cada termo na integral. Isso nos permitirá calcular os valores esperados para qualquer variável que possamos representar por um operador.
O operador de energia
Podemos deduzir e verificar o operador de energia da mesma maneira.
O Operador de Posição
E sobre o operador de posição , ![]() ? A resposta é simplesmente
? A resposta é simplesmente
quando estamos trabalhando no espaço de posição com (como vimos acima). 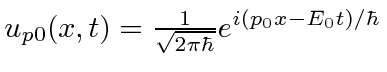
O operador hamiltoniano
Podemos desenvolver outros operadores usando os básicos. Usaremos o operador hamiltoniano que, para nossos propósitos, é a soma das energias cinética e potencial. Este é o caso não relativístico.
Uma vez que a energia potencial depende apenas de ![]() , é fácil de usar. Posteriormente, os operadores de momento angular serão simplesmente calculados a partir dos operadores de posição e momento.
, é fácil de usar. Posteriormente, os operadores de momento angular serão simplesmente calculados a partir dos operadores de posição e momento.
Operadores em espaço de impulso
Se quisermos trabalhar no espaço de momento , precisamos olhar para os estados de posição definida para encontrar nossos operadores. O estado (no espaço de momento) com posição definida ![]() é
é
Os operadores são
e
A 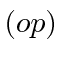 notação usada acima geralmente é eliminada. Se virmos a variável
notação usada acima geralmente é eliminada. Se virmos a variável ![]() , o uso do operador está implícito (exceto no estado escrito em termos de
, o uso do operador está implícito (exceto no estado escrito em termos de ![]() similar
similar 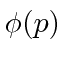 ).
).
Gasiorowicz Capítulo 3
Griffiths não cobre isso.
Cohen-Tannoudji et al. Capítulo
Expectativa de Valores
Os operadores nos permitem calcular o valor esperado de alguma grandeza física dada a função de onda. Se uma partícula está no estado 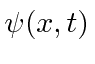 , a maneira normal de calcular o valor esperado de
, a maneira normal de calcular o valor esperado de 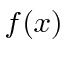 é
é
Podemos alternar 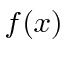 antes de
antes de ![]() antecipar o uso de operadores lineares.
antecipar o uso de operadores lineares.
Se a variável que desejamos calcular o valor esperado de (como ![]() ) não é uma função simples de
) não é uma função simples de ![]() , deixe seu operador agir
, deixe seu operador agir 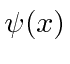 . O valor esperado
. O valor esperado ![]() do estado
do estado![]() é
é
A notação Dirac Bra-ket mostrada acima é uma maneira conveniente de representar o valor esperado de uma variável dado algum estado.
* Exemplo: uma partícula está no estado . Qual é o valor da expectativa de ? 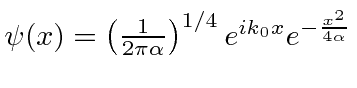
![]() *
*
Para qualquer quantidade física ![]() , o valor esperado de
, o valor esperado de ![]() em um estado arbitrário
em um estado arbitrário ![]() é
é
Os valores esperados das quantidades físicas devem ser reais .
Gasiorowicz Capítulo 3
Griffiths Capítulo 1
Cohen-Tannoudji et al. Capítulo
Notação Dirac Bra-ket
Um estado com momentum definido ![]() . Um estado com posição definida . O `` produto escalar '' entre dois estados abstratos e .
. Um estado com posição definida . O `` produto escalar '' entre dois estados abstratos e . ![]()
![]()
![]()
![]()
![]()
Este produto escalar projeta o estado ![]() para
para ![]() e representa a amplitude de ir de
e representa a amplitude de ir de ![]() para
para ![]() .
.
Para encontrar a amplitude de probabilidade de nossa partícula em qualquer posição ![]() , pontilhamos o estado de definido
, pontilhamos o estado de definido ![]() em nosso estado
em nosso estado ![]() .
. 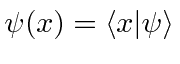
Para encontrar a amplitude de probabilidade de nossa partícula ter um momento ![]() , pontilhamos o estado de definido
, pontilhamos o estado de definido ![]() em nosso estado
em nosso estado ![]() .
. 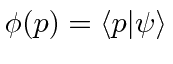
Comutadores
Operadores (ou variáveis na mecânica quântica) não necessariamente comutam. Podemos ver nosso primeiro exemplo disso agora que temos alguns operadores. Nós definimos o comutador para ser
Vamos agora calcular o comutador entre ![]() e
e ![]() . Por
. Por ![]() ser representado por um operador diferencial, devemos fazer isso com cuidado. Vamos pensar no comutador também como um operador (diferencial), como geralmente será. Para garantir que manteremos tudo de que precisamos, calcularemos e removeremos o no final para ver apenas o comutador.
ser representado por um operador diferencial, devemos fazer isso com cuidado. Vamos pensar no comutador também como um operador (diferencial), como geralmente será. Para garantir que manteremos tudo de que precisamos, calcularemos e removeremos o no final para ver apenas o comutador. ![]()
![\ bgroup \ color {black} $ [p, x] \ psi (x) $ \ egroup](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1006.png)
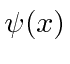
Então, removendo o 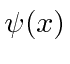 que usamos para fins computacionais, obtemos o comutador.
que usamos para fins computacionais, obtemos o comutador.
Mais tarde, aprenderemos a derivar a relação de incerteza para duas variáveis de seu comutador. Variáveis físicas com comutador zero não têm princípio de incerteza e podemos conhecer os dois ao mesmo tempo.
Também usaremos comutadores para resolver vários problemas importantes.
Podemos calcular o mesmo comutador no espaço de momento .
O comutador é o mesmo em qualquer representação.
* Exemplo: calcule o comutador ![$ [E, t] $](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1010.png) . *
. *
* Exemplo: Calcule o comutador ![$ [E, x] $](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1011.png) . *
. *
* Exemplo: Calcule o comutador ![$ [p, x ^ n] $](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1012.png) . *
. *
* Exemplo: Calcule o comutador dos operadores de momento angular ![$ [L_x, L_y] $](https://quantummechanics.ucsd.edu/ph130a/130_notes/img30.png) . *
. *
Gasiorowicz Capítulo 3
Griffiths Capítulo 3
Cohen-Tannoudji et al. Capítulo
Derivações e Cálculos
Operador de verificação de impulso
Verify Energy Operator
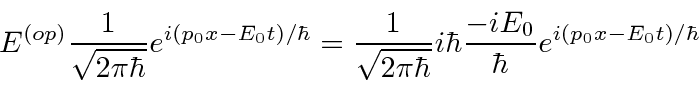
Valor de expectativa de momentum em um determinado estado
Uma partícula está no estado . Qual é o valor da expectativa de ? 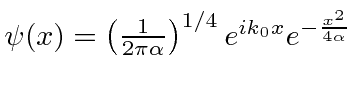
![]()
Usaremos o operador momentum para obter esse resultado.
O segundo termo dá zero porque a integral é estranha ![]() .
.
Excelente.
Comutador de 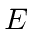 e
e 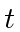
Mais uma vez, use a muleta de manter uma função de onda à direita para evitar erros.
Removendo a função de onda, temos o comutador.
Comutador de 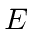 e
e 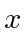
Mais uma vez, use a muleta de manter uma função de onda à direita para evitar erros.
Comutador de 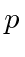 e
e 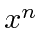
Podemos usar o comutador ![\ bgroup \ color {black} $ [p, x] $ \ egroup](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1025.png) para nos ajudar. Lembre-se disso
para nos ajudar. Lembre-se disso ![\ bgroup \ color {black} $ px = xp + [p, x] $ \ egroup](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1026.png) .
.
Normalmente não é aconselhável usar os operadores diferenciais e uma muleta de função de onda para calcular comutadores como este. Use os comutadores básicos conhecidos quando puder. No entanto, podemos calcular dessa forma.
Funciona muito bem para este caso em particular, mas não se eu tiver ![]() algum poder ...
algum poder ...
Comutador de 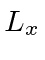 e
e 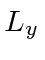
O momento angular é definido por
Portanto, os componentes do momento angular são
Queremos calcular ![\ bgroup \ color {black} $ [L_x, L_y] $ \ egroup](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1036.png) qual possui todas as coordenadas e momentos.
qual possui todas as coordenadas e momentos.
Os únicos operadores que não comutam são as coordenadas e seus momentos conjugados.
Portanto, agora só precisamos calcular.
Não é necessário (ou sábio) usar os operadores diferenciais e uma muleta de função de onda para calcular comutadores como este. Use os comutadores básicos conhecidos quando puder.
Problemas de teste de amostra
- O quadrado absoluto de uma função de onda para uma partícula livre é dado como:
Encontre o valor esperado de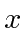 em função do tempo. Encontre o valor esperado de
em função do tempo. Encontre o valor esperado de 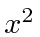 em função do tempo. Calcule a largura x RMS desse pacote de ondas em função do tempo.
em função do tempo. Calcule a largura x RMS desse pacote de ondas em função do tempo. - Encontre o comutador onde é uma constante e o segundo operador pode ser expandido como .
![$ [p, e ^ {ik_0 x}] $](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1043.png)
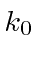
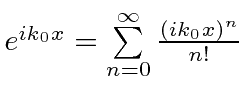
- Quais das opções a seguir são operadores lineares?
- Para uma partícula livre, o operador de energia total H é dado por
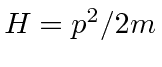 . Calcule os comutadores [H, x] e [H, p]. Se uma partícula está em um estado de energia definida, o que esses comutadores dizem sobre quão bem conhecemos a posição e o momento da partícula?
. Calcule os comutadores [H, x] e [H, p]. Se uma partícula está em um estado de energia definida, o que esses comutadores dizem sobre quão bem conhecemos a posição e o momento da partícula? - Encontre o comutador
![$ [x, p ^ 3] $](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1051.png) .
. - Calcule o comutador
![$ [H, x ^ 2] $](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1052.png) onde
onde 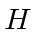 é o Hamiltoniano de uma partícula livre.
é o Hamiltoniano de uma partícula livre.
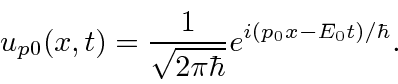
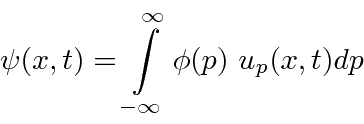
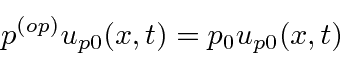
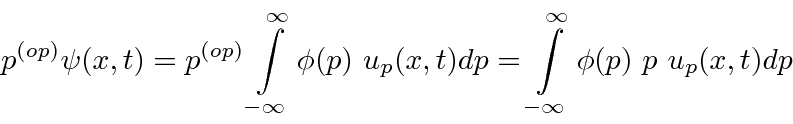
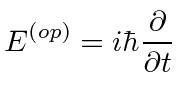
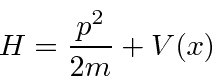
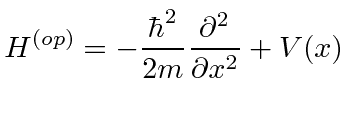
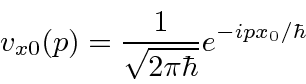
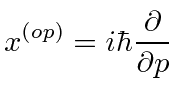
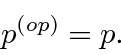
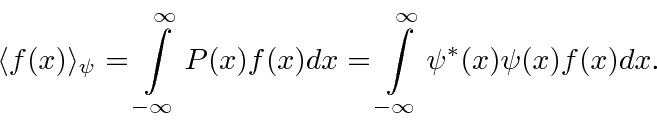
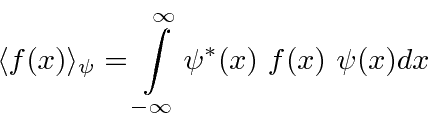
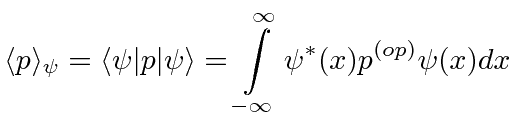
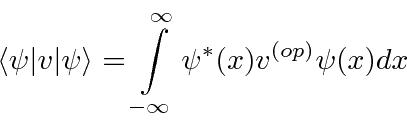
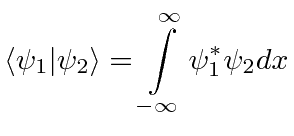
![\ bgroup \ color {black} $ \ displaystyle [p, x] \ equiv px-xp $ \ egroup](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1005.png)
![\ begin {eqnarray *} [p, x] \ psi (x) & = & px \ psi (x) -xp \ psi (x) = {\ hbar \ over i} {\ partial \ ove ... ... \ parcial \ psi (x) \ over \ partial x} \ right) = {\ hbar \ over i} \ psi (x) \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1007.png)
![\ bgroup \ color {black} $ \ displaystyle [p, x] = {\ hbar \ over i} $ \ egroup](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1008.png)
![\ begin {eqnarray *} [p, x] \ phi & = & [p, i \ hbar {d \ over dp}] \ phi = i \ hbar \ left (p {d \ over dp} \ ... .. . = i \ hbar (- \ phi) = {\ hbar \ over i} \ phi \\ {[p, x]} & = & {\ hbar \ over i} \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1009.png)
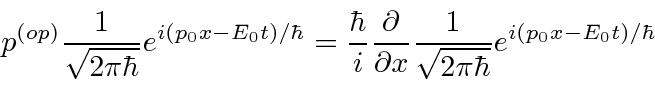
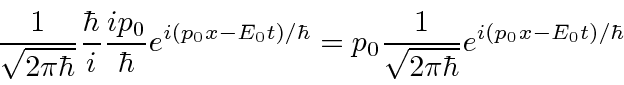
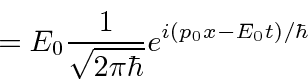

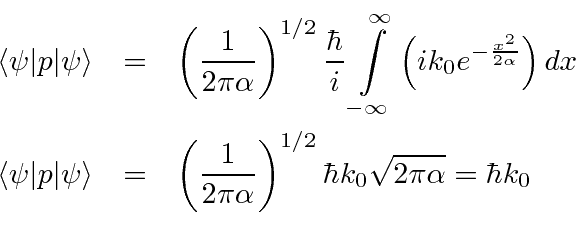
![\ begin {eqnarray *} [E, t] \ psi (x, t) & = & \ left (i \ hbar {\ partial \ over \ partial t} t-ti \ hba ... ... rtial \ over \ parcial t} \ direita) \ psi (x, t) \\ & = & i \ hbar \ psi (x, t) \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1020.png)
![\ begin {displaymath} \ bgroup \ color {black} [E, t] = i \ hbar \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1021.png)
![\ begin {eqnarray *} [E, x] \ psi (x, t) & = & \ left (i \ hbar {\ partial \ over \ partial t} x-xi \ hba ... ... ial t} -i \ hbar x {\ partial \ over \ partial t} \ right) \ psi (x, t) = 0 \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1022.png)
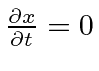
![\ begin {eqnarray *} [p, x ^ n] & = & px ^ nx ^ np \\ & = & (px) x ^ {n-1} -x ^ np \\ & = & xpx ^ {n-1} + [p ... ... p, x] x ^ {n-1} -x ^ np \\ & = & n [p, x] x ^ {n-1} = n {\ hbar \ sobre i} x ^ {n-1} \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1027.png)
![\ begin {displaymath} \ bgroup \ color {black} [p, x ^ n] \ psi = {\ hbar \ over i} {\ partial \ over \ ... ... {\ partial \ over \ partial x} \ psi = {\ hbar \ over i} nx ^ {n-1} \ psi \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1028.png)
![\ begin {displaymath} \ bgroup \ color {black} [p, x ^ n] = {\ hbar \ over i} nx ^ {n-1} \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1029.png)
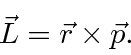
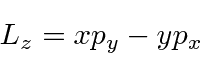
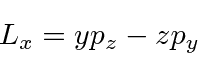
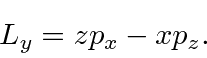
![\ begin {displaymath} \ bgroup \ color {black} [x, y] = 0 \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1037.png)
![\ begin {displaymath} \ bgroup \ color {black} [p_x, p_y] = 0 \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1038.png)
![\ begin {displaymath} \ bgroup \ color {black} [p_i, r_j] = {\ hbar \ over i} \ delta_ {ij} \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1039.png)
![\ begin {eqnarray *} [L_x, L_y] & = & [yp_z-zp_y, zp_x-xp_z] \\ & = & [yp_z, zp_x] - [yp_z, xp_z ... ...- 0-0 + x [z, p_z] p_y \\ & = & {\ hbar \ over i} (yp_x-xp_y) = i \ hbar L_z \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1040.png)