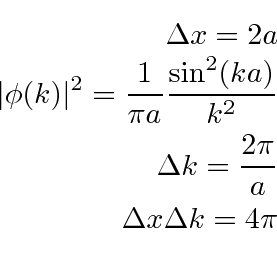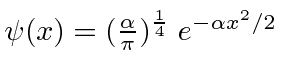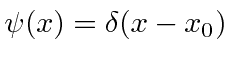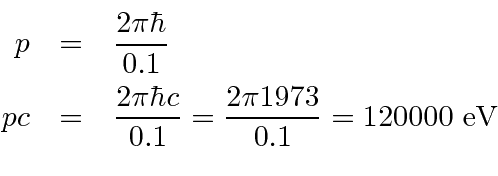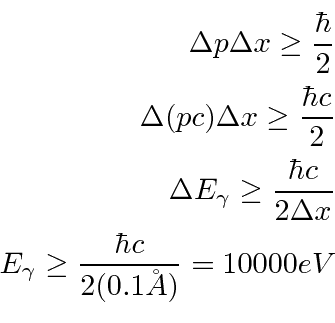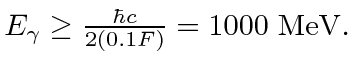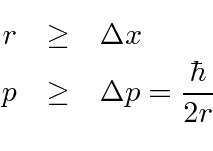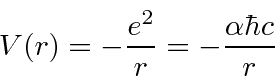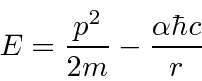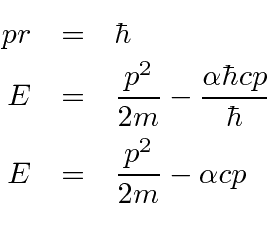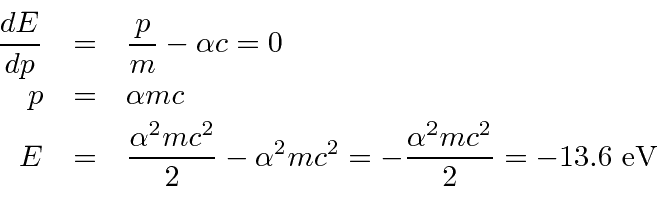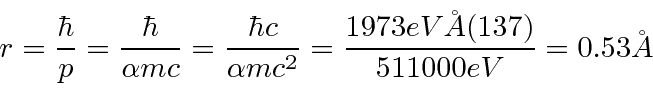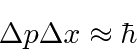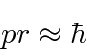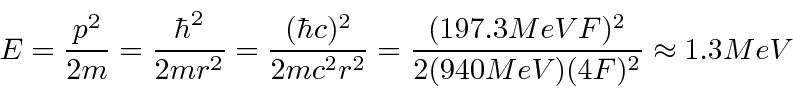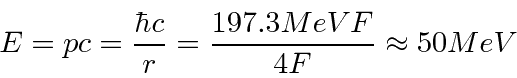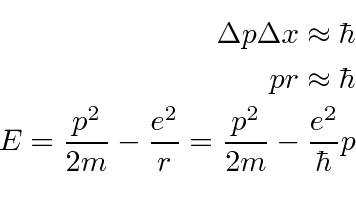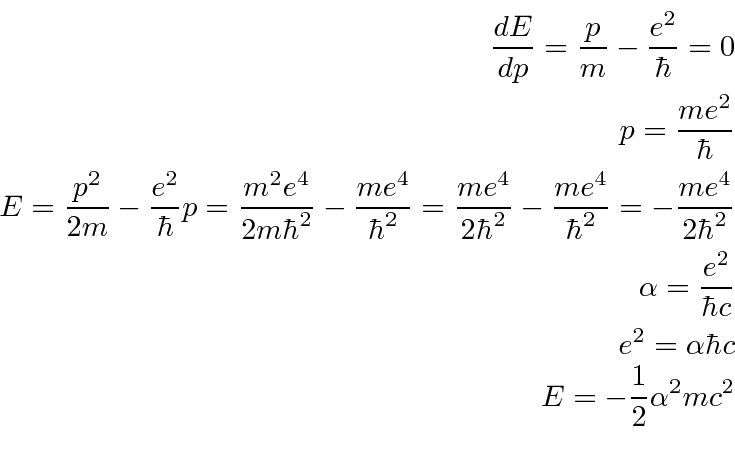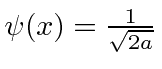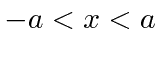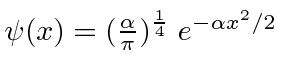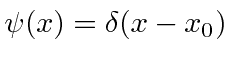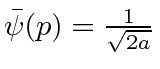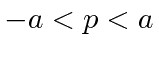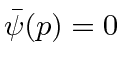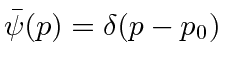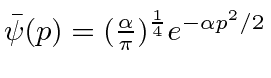Gasiorowicz Capítulo 2
Capítulos 5 de Rohlf
Griffiths Capítulo 2
Cohen-Tannoudji et al. Capítulo
Construindo um pacote de onda de partícula única localizada
Agora temos uma função de onda para uma partícula livre com um momento definido ![]()
onde o número de onda ![]() é definido por
é definido por 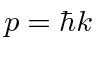 e a frequência angular
e a frequência angular ![]() satisfaz
satisfaz ![]() . Não está localizado em todos os lugares.
. Não está localizado em todos os lugares. 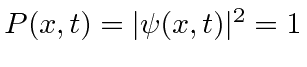
Gostaríamos de um estado localizado e normalizado para uma partícula .
Para fazer um pacote de ondas localizado no espaço , devemos adicionar componentes de diferentes números de onda. Lembre-se de que podemos usar uma série de Fourier para compor qualquer função 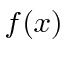 quando limitamos o intervalo a
quando limitamos o intervalo a 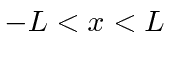 . Não queremos limitar nossos estados em
. Não queremos limitar nossos estados em ![]() , então vamos tirar o limite disso . Nesse limite, todo número de onda é permitido para que a soma se transforme em uma integral. O resultado é a transformada de Fourier intimamente relacionada
, então vamos tirar o limite disso . Nesse limite, todo número de onda é permitido para que a soma se transforme em uma integral. O resultado é a transformada de Fourier intimamente relacionada ![]()
com coeficientes que são computáveis,
As normalizações de 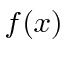 e
e 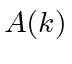 são iguais (com esta forma simétrica ) e ambas podem representar amplitudes de probabilidade.
são iguais (com esta forma simétrica ) e ambas podem representar amplitudes de probabilidade.
Entendemos 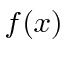 como um pacote de ondas composto de termos de momentum definidos
como um pacote de ondas composto de termos de momentum definidos ![]() . O coeficiente de cada termo é
. O coeficiente de cada termo é 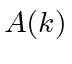 . A probabilidade de uma partícula ser encontrada em uma região em
. A probabilidade de uma partícula ser encontrada em uma região em ![]() torno de algum valor
torno de algum valor ![]() é
é 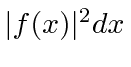 . A probabilidade de uma partícula ter um número de onda na região em
. A probabilidade de uma partícula ter um número de onda na região em ![]() torno de algum valor de
torno de algum valor de ![]() é
é 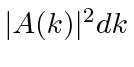 . (Lembre-se de que
. (Lembre-se de que 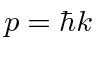 a distribuição do momentum está intimamente relacionada. Trabalhamos com isso
a distribuição do momentum está intimamente relacionada. Trabalhamos com isso ![]() por um tempo para economia de notação.)
por um tempo para economia de notação.)
Dois exemplos de pacotes de ondas localizados
Vamos agora tentar dois exemplos de um pacote de ondas localizado ![]() e normalizado corretamente em
e normalizado corretamente em ![]() .
.
Ambos estão localizados em relação ao momento 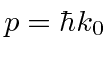 .
.
Verifique a normalização de (1).
Verifique a normalização de (2) usando o resultado para uma integral definida de um Gaussiano 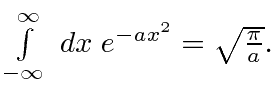
Portanto, agora pegamos a transformada de Fourier de (1) bem aqui.
Observe que é igual a 1 em e que diminui a partir daí. Se você quadrar isso, deve lembrá-lo de um padrão de difração de fenda única! Na verdade, a única fenda nos dá uma localização quadrada no espaço de posição e o FT é essa função. 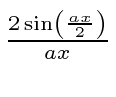
![]()
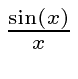
A transformada de Fourier de um pacote de onda gaussiana é 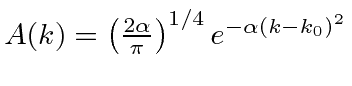
também um gaussiano. Mostraremos mais tarde que um gaussiano é o melhor que se pode fazer para localizar uma partícula em posição e momento ao mesmo tempo.
Em ambos os casos de 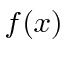 (transformado de um normalizado
(transformado de um normalizado 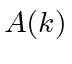 localizado no espaço de momento), vemos
localizado no espaço de momento), vemos
- Um coeficiente que normaliza corretamente o estado para 1,
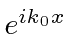 - uma onda correspondente ao momento
- uma onda correspondente ao momento 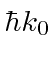 ,
,- e uma função de pacote localizada em
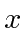 .
.
Alcançamos nosso objetivo de encontrar estados que representam uma partícula livre . Vemos que podemos ter estados localizados tanto no espaço de posição quanto no espaço de momento. Conseguimos isso criando pacotes de ondas que são sobreposições de estados com momento definido. Os pacotes de ondas, embora localizados, têm alguma largura dentro ![]() e fora
e fora ![]() .
.
O Princípio da Incerteza de Heisenberg
Os pacotes de ondas que testamos acima satisfazem um princípio de incerteza, que é uma propriedade das ondas . Isso é . 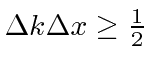
Para o pacote `` quadrado '', a largura total em ![]() é
é ![]() . A largura em
. A largura em ![]() é um pouco difícil de definir, mas vamos usar o primeiro nó na probabilidade encontrada em ou . Portanto, a largura é o dobro disso ou . Isso nos dá
é um pouco difícil de definir, mas vamos usar o primeiro nó na probabilidade encontrada em ou . Portanto, a largura é o dobro disso ou . Isso nos dá 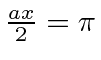
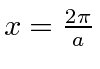
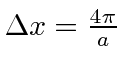
o que certamente satisfaz o limite acima. Observe que, se alterarmos a largura de 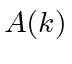 , a largura das
, a largura das 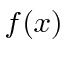 alterações para manter o produto de incerteza constante.
alterações para manter o produto de incerteza constante.
Para o pacote de onda gaussiana, podemos ler rigorosamente a largura RMS da distribuição de probabilidade, como foi feito no final da seção sobre a transformada de Fourier de uma gaussiana.
Podemos ver novamente que, conforme variamos a largura no espaço k, a largura no espaço x varia para manter o produto constante.
O pacote de ondas gaussianas fornece a incerteza mínima . Vamos provar isso mais tarde.
Se traduzirmos em momentum 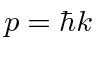 , então
, então
Assim afirma o Princípio da Incerteza de Heisenberg .
Diz que não podemos saber a posição de uma partícula e seu momento ao mesmo tempo e nos diz o limite de quão bem podemos conhecê-los.
Se tentarmos localizar uma partícula em uma região muito pequena do espaço, seu momento torna-se incerto. Se tentarmos fazer uma partícula com um momento definido, sua distribuição de probabilidade se espalha no espaço.
Espaço de posição e espaço de impulso
Podemos representar um estado com 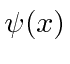 ou com
ou com 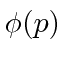 . Podemos (Fourier) nos transformar de um para o outro.
. Podemos (Fourier) nos transformar de um para o outro.
Temos a Transformada de Fourier simétrica.
Quando mudamos a variável de ![]() para
para ![]() , obtemos as transformadas de Fourier em termos de
, obtemos as transformadas de Fourier em termos de ![]() e
e![]() .
.
Vale a pena estudar essas fórmulas. Se definirmos 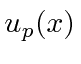 ser o estado com momentum definido
ser o estado com momentum definido ![]() , (no espaço de posição) nossa fórmula para isso é
, (no espaço de posição) nossa fórmula para isso é
Da mesma forma, o estado (no espaço momentum) com posição definida ![]() é
é
Esses estados não podem ser normalizados para 1, mas eles têm uma convenção de normalização que é satisfeita devido à constante mostrada.
Nossa transformada de Fourier agora pode ser lida para dizer que somamos estados de momentum definido para obter 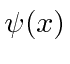
e somamos estados de posição definida a serem obtidos 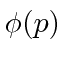 .
.
Existe uma maneira mais abstrata de escrever esses estados. Usando a notação de Dirac, o estado com momentum definido ![]() , pode ser escrito como
, pode ser escrito como 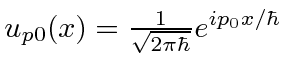
e o estado com posição definida ![]() , pode ser escrito
, pode ser escrito 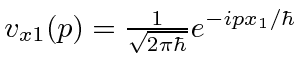
O estado arbitrário representado por 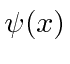 ou
ou 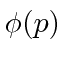 , pode ser escrito simplesmente como
, pode ser escrito simplesmente como
A função de onda real 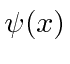 seria escrita como
seria escrita como
Isso nos dá a amplitude necessária ![]() para qualquer valor de
para qualquer valor de ![]() .
.
Descobriremos que existem outras maneiras de representar os estados quânticos. Esta foi uma prévia. Passaremos mais tempo na notação de Dirac Bra-ket mais tarde.
Desenvolvimento de tempo de um pacote de onda gaussiana *
Até agora, executamos nossas transformadas de Fourier ![]() e analisamos o resultado apenas em
e analisamos o resultado apenas em ![]() . Agora vamos colocar o tempo de volta na função de onda e olhar para o pacote de ondas mais tarde. Veremos que o comportamento dos fótons e dos elétrons não relativísticos é bem diferente.
. Agora vamos colocar o tempo de volta na função de onda e olhar para o pacote de ondas mais tarde. Veremos que o comportamento dos fótons e dos elétrons não relativísticos é bem diferente.
Suponha que comecemos com nosso pacote de ondas Gaussiano (incerteza mínima) em . Podemos fazer a transformada de Fourier para posicionar o espaço, incluindo a dependência do tempo. 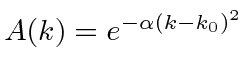
![]()
Escrevemos explicitamente de que ![]() depende
depende ![]() . Para nossa partícula livre, isso significa apenas que a energia depende do momento. Para um fóton,
. Para nossa partícula livre, isso significa apenas que a energia depende do momento. Para um fóton, 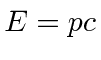 então e daí . Para um elétron não relativístico,, portanto , e portanto .
então e daí . Para um elétron não relativístico,, portanto , e portanto . ![]()
![]()
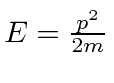
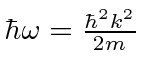
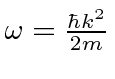
Para cobrir o caso geral, vamos expandir em 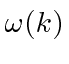 torno do centro do pacote de ondas no espaço k.
torno do centro do pacote de ondas no espaço k.
Antecipamos um pouco o resultado e nomeamos os coeficientes.
Para o fóton 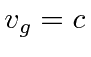 e
e 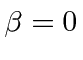 . Para o elétron NR, e .
. Para o elétron NR, e . 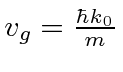
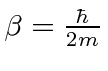
Realizando a Transformada de Fourier, obtemos
Vemos que o fóton se moverá com a velocidade da luz e que o pacote de ondas não se dispersará, porque 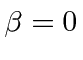 .
.
Para o electrão NR, o pacote de ondas move-se com a correcta velocidade de grupo , , mas o pacote de ondas espalha com o tempo . A largura RMS é . 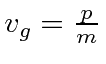
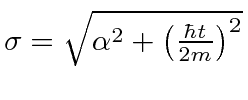
Um pacote de ondas se espalha naturalmente porque contém ondas de momentos diferentes e, portanto, de velocidades diferentes. Pacotes de ondas muito localizados no espaço se espalham rapidamente.
Derivações e cálculos
Fourier Series
As séries de Fourier nos permitem expandir qualquer função periódica no intervalo 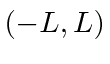 , em termos de senos e cossenos também periódicos nesse intervalo.
, em termos de senos e cossenos também periódicos nesse intervalo.
Uma vez que os senos e cossenos podem ser feitos a partir das exponenciais complexas, podemos igualmente usá-los para nossa base de expansão. Isso tem a boa simplificação de ter apenas um termo na soma, usando negativo ![]() para obter o outro termo.
para obter o outro termo.
Os exponenciais são ortogonais e normalizados no intervalo (assim como os senos e cossenos)
para que possamos calcular facilmente os coeficientes.
Em resumo, as equações da série de Fourier que usaremos são
e
Vamos expandir o intervalo ao infinito.
Transformada de Fourier *
Para permitir que as funções de onda se estendam ao infinito , vamos expandir o intervalo usado
Ao fazermos isso, usaremos o número da onda
Como , pode assumir qualquer valor, o que implica que teremos uma distribuição contínua de . Nossa soma torna - se integral . ![]()
![]()
![]()
![]()
![]()
Se definirmos , podemos fazer a transformação sair com as constantes que desejamos. 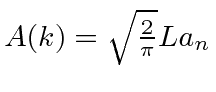
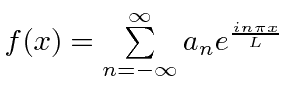 |
Série Fourier Padrão |
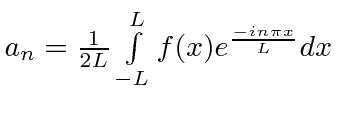 |
Série Fourier Padrão |
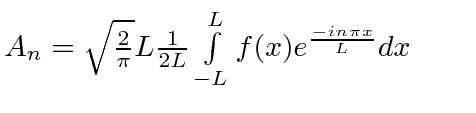 |
redefinir coeficiente |
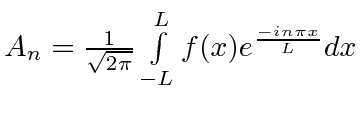 |
|
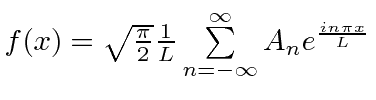 |
f continua o mesmo |
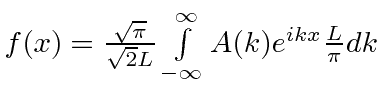 |
mas é reescrito em novo A e dk |
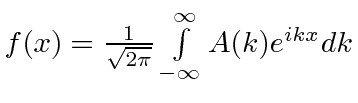 |
resultado |
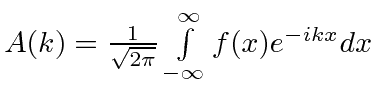 |
resultado |
Esta é apenas a extensão da série Fourier para todos ![]() .
.
Se 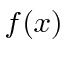 for normalizado, então
for normalizado, então 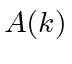 também será normalizado com esta forma (simétrica) da Transformada de Fourier. Assim, se
também será normalizado com esta forma (simétrica) da Transformada de Fourier. Assim, se 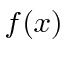 é uma amplitude de probabilidade no espaço de posição,
é uma amplitude de probabilidade no espaço de posição, 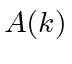 pode ser uma amplitude de probabilidade (no espaço k).
pode ser uma amplitude de probabilidade (no espaço k).
Integral de Gauss
Esta é apenas uma derivação escorregadia da integral definida de uma Gaussiana de menos infinito a infinito. Com outros limites, o integral não pode ser feito analiticamente, mas é tabulado. As funções estão disponíveis em bibliotecas de computador para retornar esta importante integral.
A resposta é
Transformada de Fourier de Gaussiana
Queremos Fourier transformar o pacote de ondas gaussianas em (momento) k-espaço para entrar no espaço de posição. A fórmula da Transformada de Fourier é 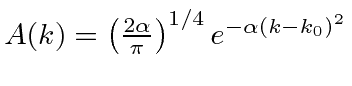
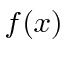
Agora vamos transformar a integral algumas vezes para chegar à integral definida padrão de uma gaussiana para a qual sabemos a resposta. Primeiro,
que realmente não faz nada desde então ![]() .
.
Agora queremos completar o quadrado do expoente dentro da integral. Planejamos um termo como definimos ![]()
Mais uma vez ![]() . Vamos escrever o expoente planejado para ver o que está faltando.
. Vamos escrever o expoente planejado para ver o que está faltando.
Precisamos multiplicar por para cancelar o termo extra no quadrado preenchido. ![]()
Esse termo pode ser extraído da integral, pois não depende de ![]() .
.
Portanto, agora temos a integral gaussiana padrão que apenas nos dá . 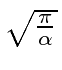
Vamos verificar a normalização .
Dado um normalizado 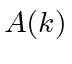 , obtemos um normalizado
, obtemos um normalizado 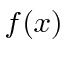 .
.
O desvio RMS ou desvio padrão de um Gaussiano pode ser lido a partir da distribuição.
Lendo tanto o coeficiente quanto o exponencial, vemos que
Para a largura no espaço k,
Lendo a partir do coeficiente do exponencial, obtemos
Podemos ver que conforme variamos a largura no espaço k, a largura no espaço x varia para manter o produto constante.
Traduzindo isso em momentum, chegamos ao limite do Princípio da Incerteza de Heisenberg .
Na verdade, o Princípio da Incerteza afirma que
então os pacotes de ondas gaussianas parecem saturar o limite!
Definir
Integrar sobre ambos ![]() e
e ![]() para que
para que
Transforme em coordenadas polares.
Agora é só obter a raiz quadrada para obter a resposta acima.
Outras formas podem ser obtidas diferenciando em relação a ![]() .
.
Dependência de tempo de um pacote de onda gaussiana
Suponha que comecemos com nosso pacote de ondas Gaussiano (incerteza mínima) em . Não estamos interessados em uma normalização cuidadosa aqui, portanto, eliminaremos as constantes.
Escrevemos explicitamente de que
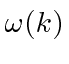 torno do centro do pacote de ondas no espaço k.
torno do centro do pacote de ondas no espaço k.
Antecipamos um pouco o resultado e nomeamos os coeficientes.
Ainda precisamos fazer a integral como antes. Faça a substituição 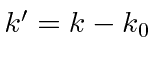 dando . Fatore o exponencial constante que não tem dependência.
dando . Fatore o exponencial constante que não tem dependência. 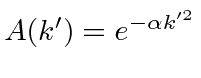
![]()
Agora comparamos essa integral com a que fizemos anteriormente (para que possamos evitar o trabalho de completar o quadrado novamente). Tirando as constantes, tínhamos
Nosso novo integrante é o mesmo com as substituições , e . Podemos então escrever a resposta
Números
A unidade conveniente de energia (massa e momento também) é o volt do elétron.
Use a constante de estrutura fina para evitar unidades CGS que são usadas no livro. Essa combinação economiza muito trabalho.
O raio de Bohr fornece o tamanho do átomo de hidrogênio.
A Função Delta de Dirac
A função delta de Dirac é zero em todos os lugares, exceto no ponto onde seu argumento é zero . Nesse ponto, é o tipo certo de infinito para que
Esta é a definição da função delta. Ele seleciona o valor da função
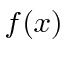 no ponto onde o argumento da função delta desaparece. Uma simples extensão da definição dá.
no ponto onde o argumento da função delta desaparece. Uma simples extensão da definição dá.
A transformação de uma integral nos permite calcular
o efeito do argumento sendo uma função.
Se fizermos um pacote de ondas no espaço p usando a função delta, e nos transformarmos no espaço de posição,
nós apenas obtemos o estado de definitivo
Este é um estado de momentum definido escrito no espaço de momentum. Sua transformada de Fourier é Este é um estado de posição definida escrito no espaço de posição.
Exemplos
O pacote de onda quadrada
Dada a seguinte amplitude de probabilidade unidimensional na variável de posição x, calcule a distribuição de probabilidade no espaço de momento. Mostre que o princípio da incerteza é aproximadamente satisfeito.
Está normalizado.
Veja a Transformada de Fourier.
Agora estime a largura das duas distribuições de probabilidade.
O Pacote de Ondas Gaussianas *
Dada a seguinte amplitude de probabilidade unidimensional na variável de posição x, calcule a distribuição de probabilidade no espaço de momento. Mostre que o princípio da incerteza é aproximadamente satisfeito.
O pacote de ondas de função delta de Dirac *
Dada a seguinte amplitude de probabilidade unidimensional na variável de posição x, calcule a distribuição de probabilidade no espaço de momento. Mostre que o princípio da incerteza é aproximadamente satisfeito.
Posso "ver'' dentro de um átomo
Para ver o interior de um átomo, devemos usar luz com comprimento de onda menor que o tamanho do átomo. Com luz normal, uma vez que uma superfície é polida até o nível de 0,25 mícron, ela parece brilhante. Você não pode mais ver defeitos. Portanto, para ver o interior do átomo, precisaríamos de luz com Å. 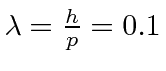
Isso é energia cinética mais do que suficiente para explodir o átomo. Você não pode `` ver '' por dentro.
Um cálculo semelhante pode ser feito com o princípio da incerteza.
A energia de ligação é 13 eV, então isso ainda vai explodi-la.
Portanto, não podemos "observar" o interior de um átomo.
Podemos sondar átomos com fótons de alta energia (por exemplo). Isso vai explodir os átomos, mas podemos usar muitos átomos do mesmo tipo. Aprendemos sobre a estrutura interna dos átomos espalhando partículas para fora deles, explodindo-os.
Posso "ver'' dentro de um núcleo
De maneira semelhante à seção anterior, a energia de ligação por núcleo é alguns MeV, portanto, também explodiremos os núcleos para olhar cuidadosamente dentro deles. Novamente, podemos apenas usar muitos núcleos para nos permitir aprender sobre a estrutura nuclear interna.
Estimar a energia do estado fundamental do hidrogênio
A razão pela qual o átomo de hidrogênio (e outros átomos) é tão grande é essencialmente o princípio da incerteza. Se o elétron 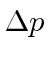 ficasse confinado a um volume menor, aumentaria, fazendo
ficasse confinado a um volume menor, aumentaria, fazendo ![]() com que aumentasse na média. A energia aumentaria, não diminuiria.
com que aumentasse na média. A energia aumentaria, não diminuiria.
Podemos usar o princípio da incerteza para estimar a energia mínima para o hidrogênio. Este não é um cálculo perfeito, mas é mais correto do que o modelo de Bohr. A ideia é que o raio deve ser maior do que o spread na posição e o momento deve ser maior do que o spread no momento.
Esta é a nossa fórmula para a energia potencial em termos da constante de estrutura fina adimensional ![]() .
.
Vamos estimar a energia
e colocar em prática o princípio da incerteza.
Diferencie em relação a ![]() e defina igual a zero para obter o mínimo.
e defina igual a zero para obter o mínimo.
Observe que a energia potencial é apenas (-2) vezes a energia cinética (como esperamos do Teorema Virial). A fórmula da energia do estado fundamental está correta.
Também podemos estimar o raio.
O estado fundamental do Hidrogênio tem momento angular zero (orbital). Não está se movendo em uma órbita circular como Bohr hipotetizou. O elétron tem apenas uma distribuição de probabilidade espalhada por cerca de 1 Å. Se não fosse espalhado, a energia aumentaria.
Problemas de teste de amostra
- Um núcleo tem um raio de 4 Fermis. Use o princípio da incerteza para estimar a energia cinética de um nêutron localizado dentro do núcleo. Faça o mesmo para um elétron.
Responder
Experimente primeiro a fórmula não relativística e verifique a aproximação quando tivermos a energia.
Isso é muito menos do que 940 MeV, então a aproximação não relativística é muito boa.A energia do elétron será maior e sua massa de repouso é de apenas 0,51 MeV, então SERÁ relativística. Isso torna tudo mais fácil.
- * Suponha que o potencial para um nêutron próximo a um núcleo pesado seja dado por
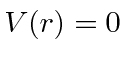 para
para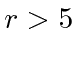 Fermis e
Fermis e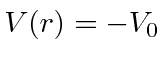 para
para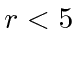 Fermis. Use o princípio da incerteza para estimar o valor mínimo
Fermis. Use o princípio da incerteza para estimar o valor mínimo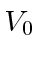 necessário para o nêutron se ligar ao núcleo.
necessário para o nêutron se ligar ao núcleo. - Use o princípio da incerteza para estimar a energia do estado fundamental do hidrogênio.
Responder
(Poderíamos ter substituído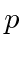 igualmente bem.) Minimize.
igualmente bem.) Minimize.
- * Dadas as seguintes amplitudes de probabilidade unidimensionais na variável de posição x, calcule a distribuição de probabilidade no espaço de momento. Mostre que o princípio da incerteza é aproximadamente satisfeito.
- Use o princípio da incerteza de Heisenberg para estimar a energia do estado fundamental para uma partícula de massa
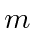 no potencial .
no potencial . 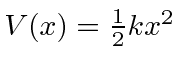
- * Encontre a função de onda unidimensional no espaço de posição
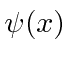 que corresponde a .
que corresponde a . 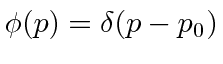
- * Encontre a função de onda unidimensional no espaço de posição
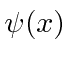 que corresponde a parae deoutra forma.
que corresponde a parae deoutra forma. 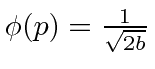
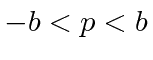
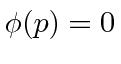
- * Suponha que uma partícula esteja localizada de tal forma queparae que em outro lugar. Qual é a probabilidade de a partícula ter um momento entree?
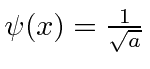
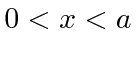
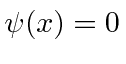
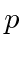
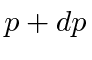
- Um feixe de fótons de momento
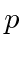 incide sobre uma fenda de largura
incide sobre uma fenda de largura 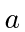 . O padrão de difração resultante é visualizado na tela, a uma distância
. O padrão de difração resultante é visualizado na tela, a uma distância 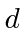 da fenda. Use o princípio da incerteza para estimar a largura do máximo central do padrão de difração em termos das variáveis fornecidas.
da fenda. Use o princípio da incerteza para estimar a largura do máximo central do padrão de difração em termos das variáveis fornecidas. - * A função de onda de uma partícula no espaço de posição é dada por. Encontre a função de onda no espaço do momento . O estado está normalizado corretamente? Explique por quê.
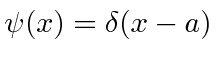
- * Uma partícula está no estado. Qual é a probabilidade de a partícula ter um momento entree?
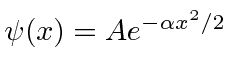
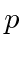
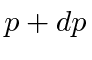
- Um átomo de hidrogênio tem potencial . Use o princípio da incerteza para estimar a energia do estado fundamental.
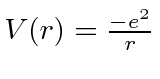
- * Suponha queparae emoutro lugar. O que é? Qual é a probabilidade de encontrar a partícula entree?
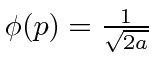
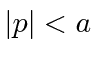
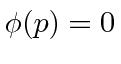
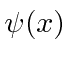
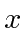
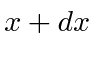
- O átomo de hidrogênio é composto de um próton e um elétron unidos pelo potencial de Coulomb ,. Também é possível fazer um átomo semelhante ao hidrogênio a partir de um próton e um múon. A força que liga o múon ao próton é idêntica à do elétron, mas a massa do múon é de 106 MeV / c . Use o princípio da incerteza para estimar a energia e o raio do estado fundamental do hidrogênio muônico.
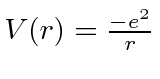
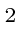
- * Dadas as seguintes amplitudes de probabilidade unidimensionais na representação do momento, calcule a amplitude da probabilidade na representação da posição
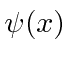 ,. Mostre que o princípio da incerteza está satisfeito.
,. Mostre que o princípio da incerteza está satisfeito.
- * Suponha isso. O que é? O que é? O que é?
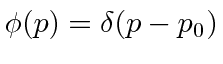
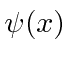
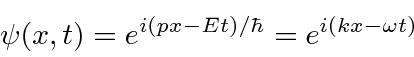
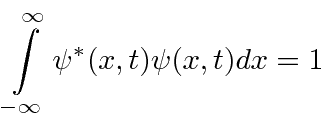
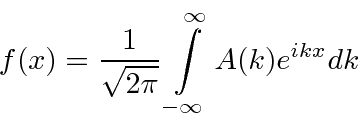
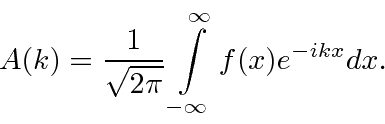
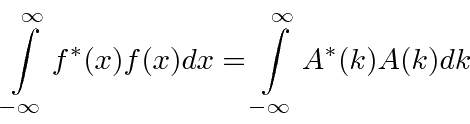
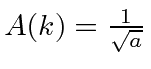
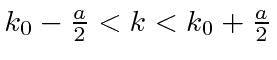
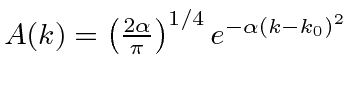
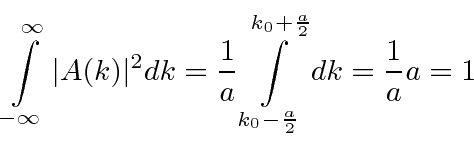
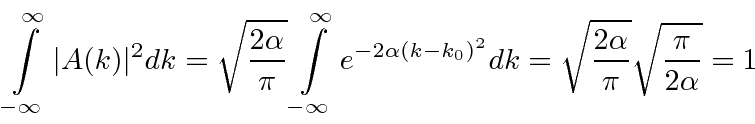
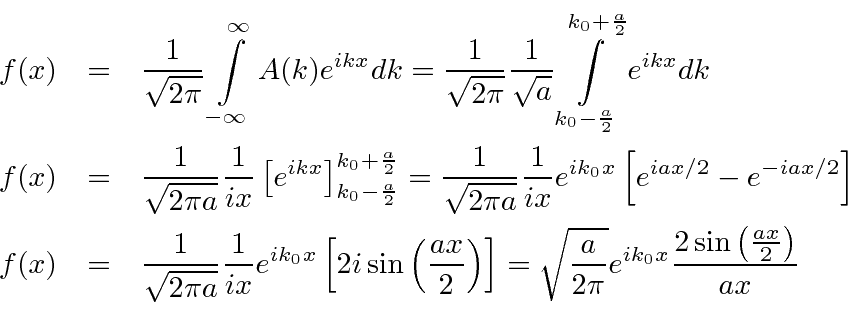
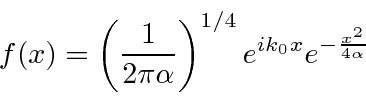
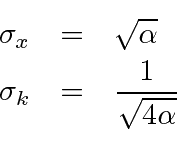
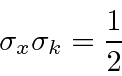
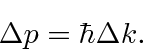
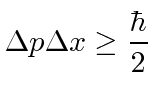
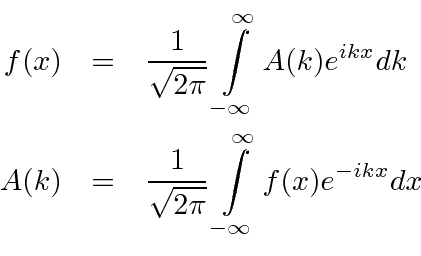
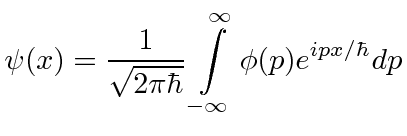
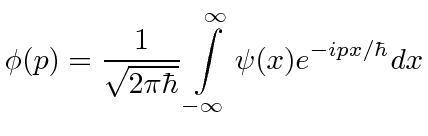
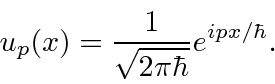
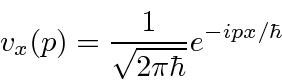
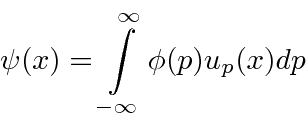
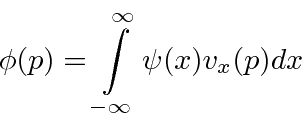
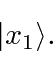
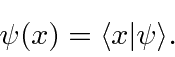
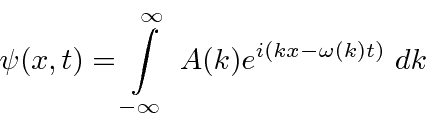
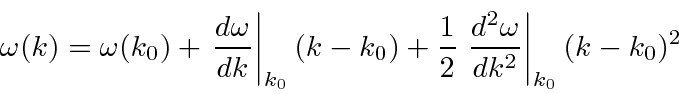
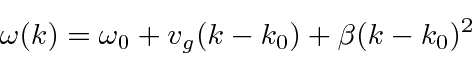
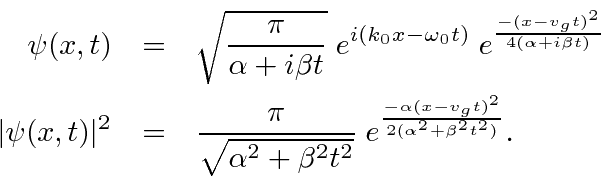
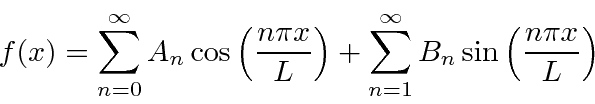
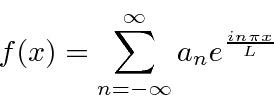
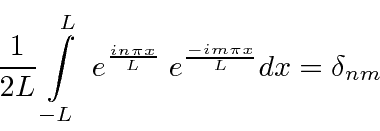
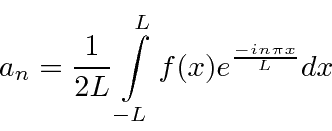
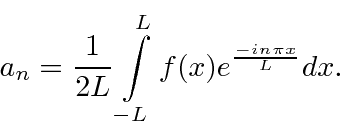
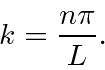
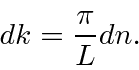
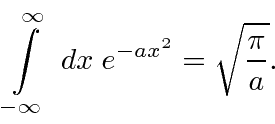
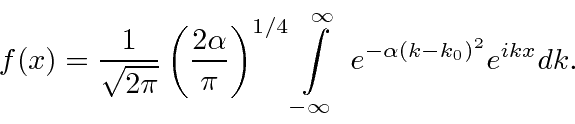
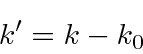
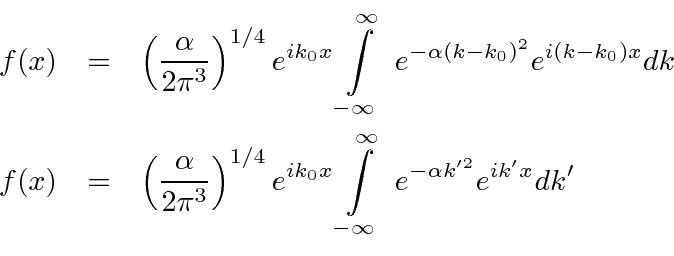
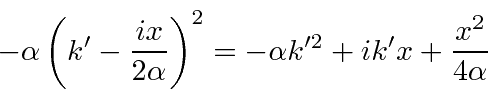
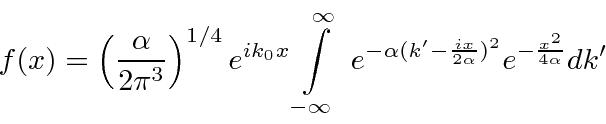
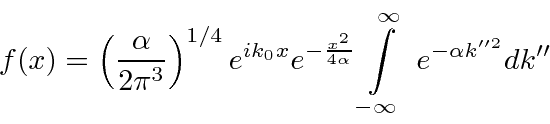
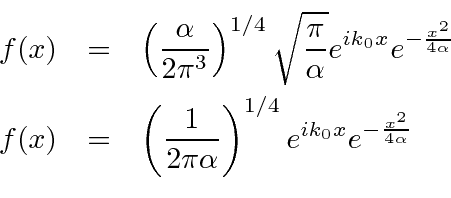
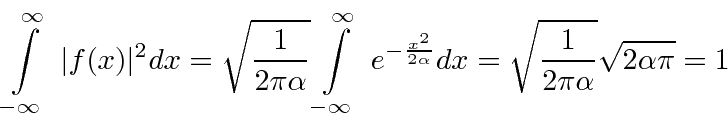
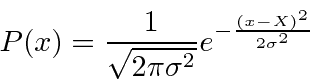
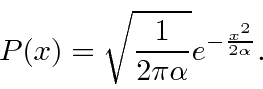
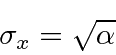
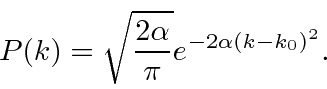
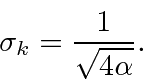
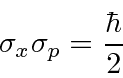
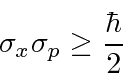
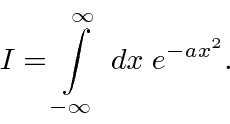
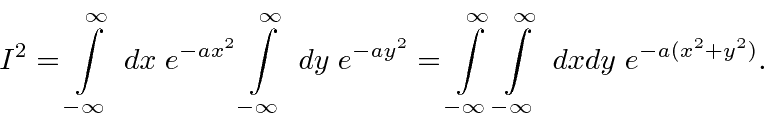
![\ begin {displaymath} \ bgroup \ color {black} I ^ 2 = 2 \ pi \ int \ limits_ {0} ^ {\ infty} \; rdr \; e ... ... i \ left [- {1 \ over a} e ^ {- ar ^ 2} \ right] _0 ^ \ infty = {\ pi \ over a} \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img865.png)
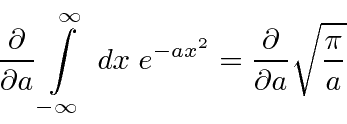
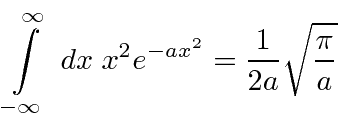
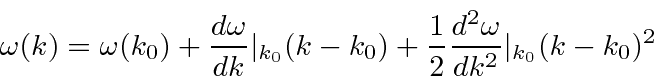
![\ begin {eqnarray *} \ psi (x, t) & = & e ^ {i (k_0x-w_0t)} \; \ int \ limits _ {- \ infty} ^ \ infty \; ... ... y} ^ \ infty \; e ^ {- [\ alpha-i \ beta t] k '^ 2} e ^ {i (k'x-v_gt)} \; dk '\\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img894.png)
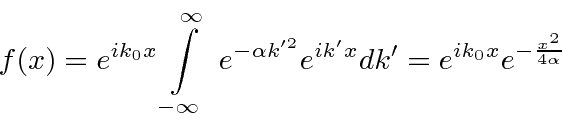
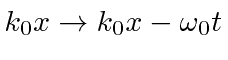
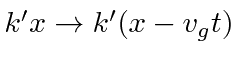
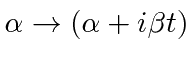
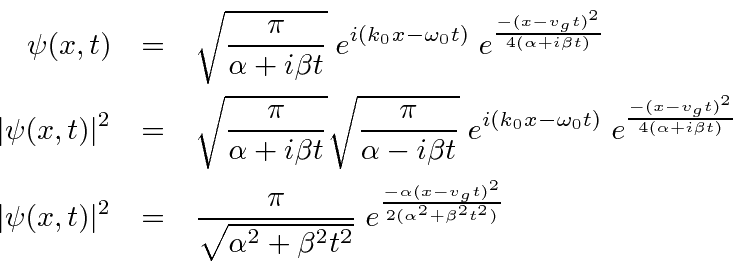
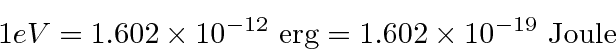
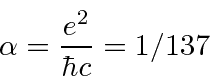
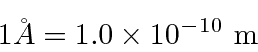
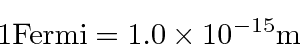
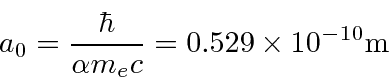
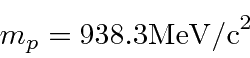
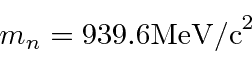
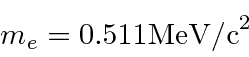
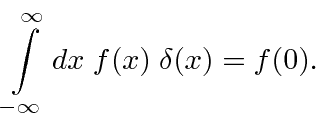
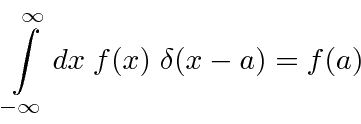
![\ begin {displaymath} \ bgroup \ color {black} \ int \ limits _ {- \ infty} ^ \ infty dx \; f (x) \; ... ... esquerda [{1 \ over \ vert {dg \ over dx} \ vert} f (x) \ right] _ {g (x) = 0} \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img911.png)
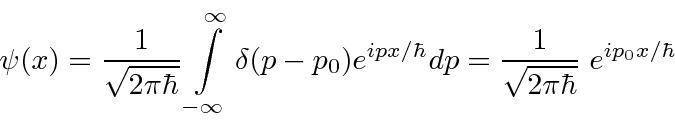
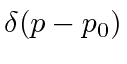
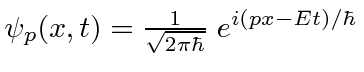
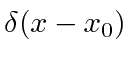
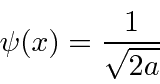
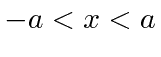
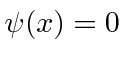
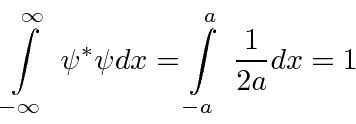
![\ begin {eqnarray *} \ phi (k) & = & {1 \ over \ sqrt {2 \ pi}} \ int \ limits _ {- a} ^ a {1 \ over \ sqrt {2 ... ... {4 \ pi a}} [- 2i \ sin {ka}] = - \ sqrt {1 \ over \ pi a} {\ sin (ka) \ over k} \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img919.png)