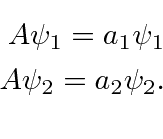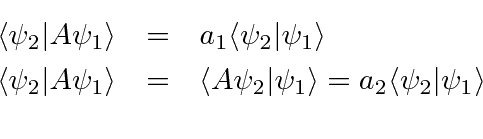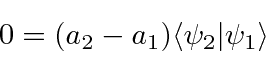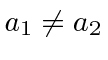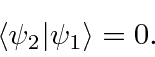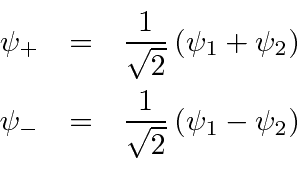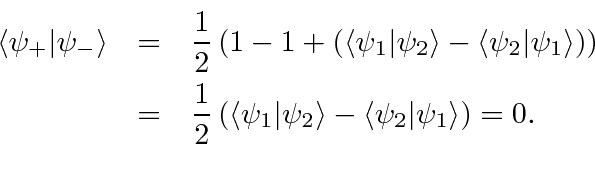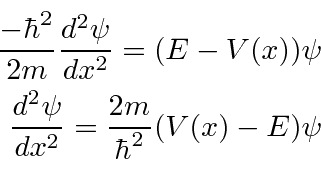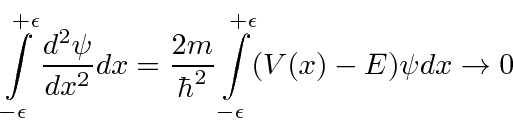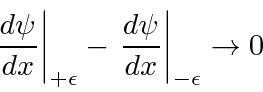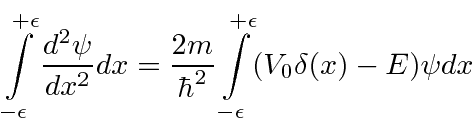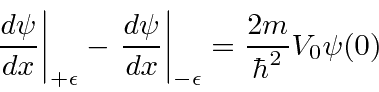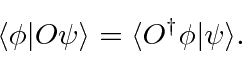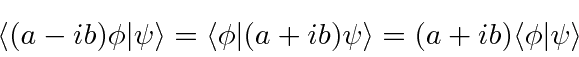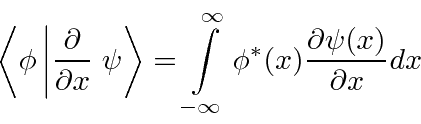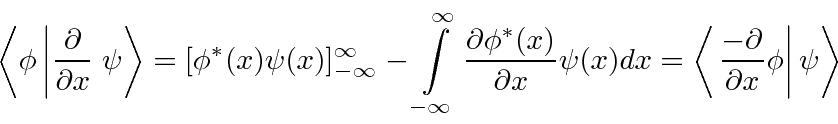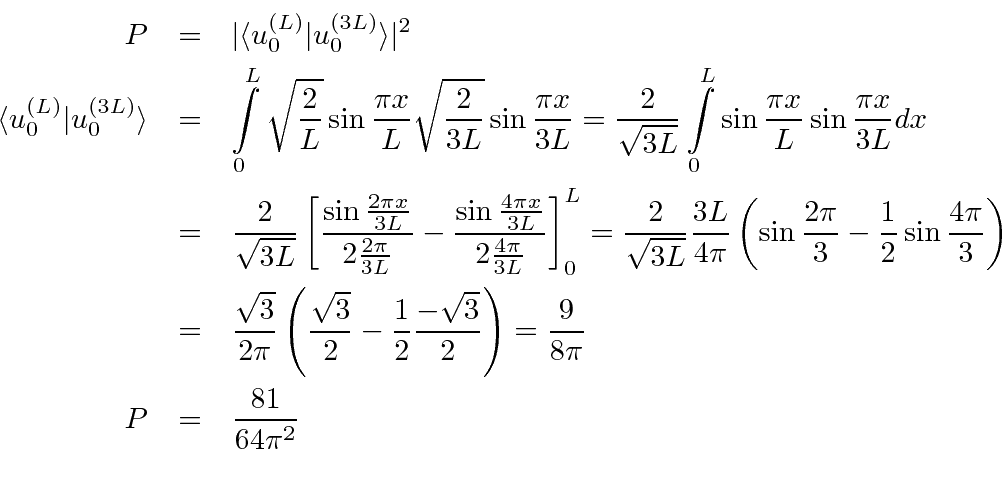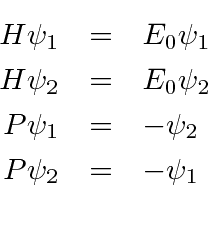Equações de autovalor
A equação de Schrödinger independente do tempo é um exemplo de uma equação de autovalor.
O hamiltoniano opera na autofunção , dando a uma constante o autovalor vezes a mesma função. (Eigen significa o mesmo em alemão.) 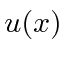
![]()
Normalmente, para estados ligados, existem muitas soluções de autofunção (denotadas aqui pelo índice ![]() ).
).
Para estados que representam uma partícula (particularmente estados ligados), devemos exigir que as soluções sejam normalizáveis . Soluções que não são normalizáveis devem ser descartadas. Uma função de onda normalizável deve ir a zero no infinito.
Na verdade, todas as derivadas de ![]() devem ir a zero no infinito para que a função de onda permaneça em zero.
devem ir a zero no infinito para que a função de onda permaneça em zero.
Vamos provar mais tarde que as autofunções são ortogonais entre si.
Assumiremos que as autofunções formam um conjunto completo de forma que qualquer função pode ser escrita como uma combinação linear delas.
(Isso pode ser comprovado por muitas das funções próprias que usaremos.)
Como as autofunções são ortogonais, podemos calcular facilmente os coeficientes na expansão de uma função de onda arbitrária ![]() .
.
Mais tarde, pensaremos nas autofunções como vetores unitários em um espaço vetorial. A função de onda arbitrária ![]() é então um vetor naquele espaço.
é então um vetor naquele espaço.
É instrutivo calcular o valor esperado do hamiltoniano usando a expansão ![]() e a ortonormalidade das autofunções.
e a ortonormalidade das autofunções.
Podemos ver que os coeficientes dos autoestados representam amplitudes de probabilidade de estar nesses estados , uma vez que os quadrados absolutos dos coeficientes obviamente fornecem a probabilidade. 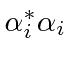
Conjugado Hermitiano de um Operador
Primeiro, vamos definir o Conjugado Hermitiano de um operador ![]() a ser
a ser ![]() . O significado deste conjugado é dado na seguinte equação.
. O significado deste conjugado é dado na seguinte equação.
Isto é, ![]() deve operar no conjugado de
deve operar no conjugado de ![]() e dar o mesmo resultado para a integral como quando
e dar o mesmo resultado para a integral como quando ![]() opera em
opera em ![]() .
.
A definição do Conjugado Hermitiano de um operador pode ser simplesmente escrita na notação Bra-Ket.
Partindo dessa definição, podemos provar algumas coisas simples. Tomando o conjugado complexo
Agora, considerando o conjugado de Hermitian ![]() .
.
Se tomarmos o conjugado Hermitiano duas vezes, voltaremos ao mesmo operador.
É fácil mostrar isso
e
apenas a partir das propriedades do produto escalar.
Nós também podemos mostrar que
* Exemplo: Encontre o conjugado hermitiano do operador 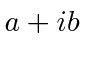 . *
. *
* Exemplo: Encontre o conjugado hermitiano do operador . ![]() *
*
Operadores Hermitianos
Uma variável física deve ter valores esperados reais (e autovalores). Isso implica que os operadores que representam variáveis físicas têm algumas propriedades especiais.
Calculando o conjugado complexo do valor esperado de uma variável física, podemos facilmente mostrar que os operadores físicos são seu próprio conjugado hermitiano .
Os operadores que são seus próprios Conjugados Hermitianos são chamados de Operadores Hermitianos .
Autofunções e espaço vetorial
As funções de onda são análogas aos vetores no espaço 3D. Os vetores unitários de nosso espaço vetorial são autoestados.
No espaço 3D normal , representamos um vetor por seus componentes.
Os vetores unitários ![]() são ortonormais,
são ortonormais,
onde ![]() é o delta de Kroneker usual, igual a 1 se
é o delta de Kroneker usual, igual a 1 se 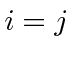 e, de outra forma, igual a zero.
e, de outra forma, igual a zero.
Autofunções - os vetores unitários de nosso espaço - são ortonormais.
Representamos nossas funções de onda - os vetores em nosso espaço - como combinações lineares de estados próprios (vetores unitários).
No espaço 3D normal, podemos calcular o produto escalar entre dois vetores usando os componentes.
Em nosso espaço vetorial, definimos o produto escalar como sendo
Também podemos calcular o produto escalar dos componentes dos vetores. Nosso espaço vetorial é um pouco diferente por causa do complexo conjugado envolvido na definição de nosso produto escalar.
De um ponto de vista mais matemático, as funções quadradas integráveis formam um Espaço de Hilbert (vetorial). O produto escalar é definido como acima.
As propriedades do produto escalar são fáceis de derivar da integral.
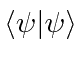 é real e maior que 0. É igual a zero sse
é real e maior que 0. É igual a zero sse 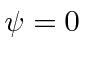 . Também podemos derivar a desigualdade de Schwartz.
. Também podemos derivar a desigualdade de Schwartz.
Operadores lineares transformam vetores no espaço em outros vetores.
A partícula em uma caixa 1D
Como um exemplo simples, resolveremos o problema 1D Particle in a Box . Essa é uma partícula confinada a uma região 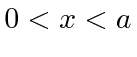 . Podemos fazer isso com o potencial (não físico) que é zero dentro desses limites e
. Podemos fazer isso com o potencial (não físico) que é zero dentro desses limites e 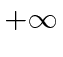 fora dos limites.
fora dos limites.
O mesmo problema com simetria de paridade
Se simplesmente redefinirmos a posição da caixa para que , nosso problema tenha simetria sob a operação de Paridade . 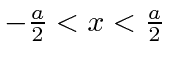
O hamiltoniano permanece inalterado se fizermos a transformação acima. O hamiltoniano comuta com o operador de paridade.
Isso significa que 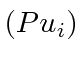 é uma autofunção de
é uma autofunção de ![]() com o mesmo autovalor de energia.
com o mesmo autovalor de energia.
Portanto, deve ser uma constante vezes a mesma autofunção de energia.
As equações dizem que as autofunções de energia também são autofunções do operador de paridade .
Se operarmos duas vezes com paridade, voltamos à função original,
portanto, os autovalores de paridade devem ser![]() .
.
As condições de limite são
Isso dá dois tipos de soluções .
Juntos, eles são exatamente equivalentes ao conjunto de soluções que tínhamos com a caixa definida para ser de 0 a![]() . Eles
. Eles 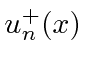 têm autovalor +1 sob o operador de paridade. Eles
têm autovalor +1 sob o operador de paridade. Eles 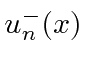 têm autovalor -1 sob o operador de paridade.
têm autovalor -1 sob o operador de paridade.
Este é um exemplo de simetria do problema, fazendo com que um operador comute com o Hamiltoniano. Podemos então ter autofunções simultâneas desse operador e ![]() . Nesse caso, todas as autofunções de energia também são aut Estados de paridade. A paridade é conservada.
. Nesse caso, todas as autofunções de energia também são aut Estados de paridade. A paridade é conservada.
Uma função de onda arbitrária pode ser escrita como uma soma das autofunções de energia recuperando a série de Fourier em sua forma padrão .
Por causa do potencial infinito, esse problema tem condições de contorno muito incomuns . (Normalmente, exigiremos a continuidade da função de onda e de sua primeira derivada.) A função de onda deve ser zero em ![]() e,
e, ![]() uma vez que deve ser contínua e é zero na região de potencial infinito. A primeira derivada não precisa ser contínua na fronteira (ao contrário de outros problemas), por causa da descontinuidade infinita no potencial.
uma vez que deve ser contínua e é zero na região de potencial infinito. A primeira derivada não precisa ser contínua na fronteira (ao contrário de outros problemas), por causa da descontinuidade infinita no potencial.
A equação de Schrödinger independente do tempo (também chamada de equação de autovalor de energia) é
com o hamiltoniano (dentro da caixa)
Nossas soluções terão
fora da caixa.
A solução dentro da caixa pode ser escrita como
onde ![]() pode ser positivo ou negativo. Precisamos escolher combinações lineares que satisfaçam a condição de contorno que .
pode ser positivo ou negativo. Precisamos escolher combinações lineares que satisfaçam a condição de contorno que . 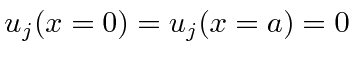
Podemos fazer isso facilmente, escolhendo
que satisfaz automaticamente o BC em 0. Para satisfazer o BC em ![]() , precisamos que o argumento de seno esteja
, precisamos que o argumento de seno esteja ![]() lá.
lá.
Conectando isso de volta à equação de Schrödinger, obtemos
Haverá apenas uma solução que satisfaça o BC para um conjunto quantizado de energias .
Temos soluções para a equação de Schrödinger que satisfazem as condições de contorno. Agora precisamos definir a constante ![]() para normalizá- los como 1.
para normalizá- los como 1.
Lembre-se de que o valor médio de ![]() é a metade (na metade dos períodos). Então, definimos
é a metade (na metade dos períodos). Então, definimos ![]() dando-nos as funções próprias
dando-nos as funções próprias
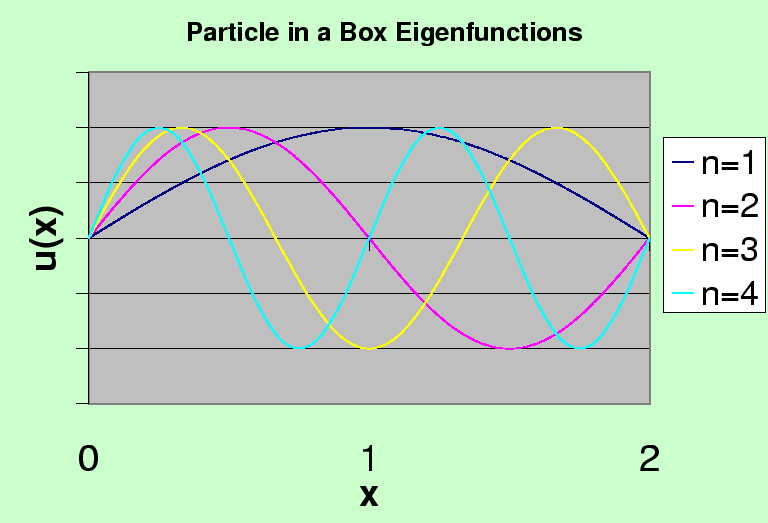
As primeiras quatro funções próprias são representadas graficamente a seguir. O estado fundamental tem a menor curvatura e o menor número de zeros da função de onda.
Observe que esses estados teriam uma paridade definida se ![]() estivessem no centro da caixa.
estivessem no centro da caixa.
A expansão de uma função de onda arbitrária nessas autofunções é essencialmente nossa Série de Fourier original . Este é um bom exemplo das autofunções de energia sendo ortogonais e cobrindo o espaço.
Autofunções do Momentum
Também podemos olhar para as autofunções do operador momentum .
Os eigenstates são
com ![]() permitido ser positivo ou negativo.
permitido ser positivo ou negativo.
Essas soluções não vão a zero no infinito, portanto não são normalizáveis para uma partícula.
Este é um problema comum para este tipo de estado.
Usaremos um tipo diferente de normalização para os autoestados de momentum (e os autoestados de posição).
Em vez do delta de Kronecker, usamos a função delta de Dirac. Os estados próprios de momentum têm uma faixa contínua de valores próprios, de modo que não podem ser indexados como os estados próprios de energia de um sistema ligado. Isso significa que o delta de Kronecker não poderia funcionar de qualquer maneira.
Estes são os auto-estados de momentum
satisfazendo a condição de normalização
Para um hamiltoniano de partícula livre , tanto o momento quanto a paridade comutam com ![]() . Portanto, podemos fazer autofunções simultâneas.
. Portanto, podemos fazer autofunções simultâneas.
Não podemos fazer autofunções de todos os três operadores, uma vez que
Portanto, temos a escolha dos ![]() estados que são autofunções de
estados que são autofunções de ![]() e de
e de ![]() , mas contêm componentes de paridade positivos e negativos. ou temos os estados
, mas contêm componentes de paridade positivos e negativos. ou temos os estados 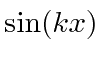 e
e 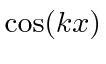 que contêm dois momentos, mas são estados próprios de
que contêm dois momentos, mas são estados próprios de ![]() e Paridade. Estas são apenas combinações lineares diferentes das mesmas soluções.
e Paridade. Estas são apenas combinações lineares diferentes das mesmas soluções.
Derivações e cálculos
As funções próprias dos operadores hermitianos são ortogonais
Queremos provar que as autofunções dos operadores Hermitianos são ortogonais. Na verdade, faremos isso primeiro, exceto no caso de autovalores iguais .
Suponha que temos um operador Hermitiano ![]() e duas de suas autofunções tais que
e duas de suas autofunções tais que
Agora calculamos de duas maneiras. 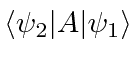
Lembre-se de que os autovalores são reais, portanto, não há necessidade de conjugação.
Agora subtraímos as duas equações . Os lados esquerdos são iguais, então eles dão zero.
As autofunções são ortogonais .
E se duas das autofunções tiverem o mesmo autovalor ? Então, nossa prova não funciona. Suponha que seja real, pois sempre podemos ajustar uma fase para torná-la real. Uma vez que qualquer combinação linear de e tem o mesmo valor próprio, podemos usar qualquer combinação linear. Nosso objetivo será escolher duas combinações lineares ortogonais . Vamos tentar 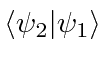
![]()
![]()
tão
Isso é zero sob a suposição de que o produto escalar é real.
Assim, encontramos um conjunto ortogonal de autofunções, mesmo no caso de alguns dos autovalores serem iguais (degenerados). De agora em diante, vamos apenas assumir que estamos trabalhando com um conjunto ortogonal de autofunções.
Continuidade de funções de onda e derivados
Podemos usar a equação de Schrödinger para mostrar que a primeira derivada da função de onda deve ser contínua , a menos que o potencial seja infinito na fronteira.
Integre ambos os lados logo abaixo de um limite (presume-se que esteja em ![]() ) até logo acima.
) até logo acima.
Deixe ![]() ir para zero e o lado direito deve ir para zero para potenciais finitos.
ir para zero e o lado direito deve ir para zero para potenciais finitos.
Potenciais infinitos não são físicos, mas geralmente são úteis. O potencial da função delta é muito útil, portanto, derivaremos uma equação de continuidade especial para ele. Suponha . Integrando a Equação de Schrödinger, obtemos 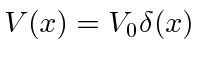
Como antes, os termos finitos na integral à direita vão para zero como , mas agora a função delta dá uma contribuição fixa para a integral. ![]()
Há uma descontinuidade na derivada da função de onda proporcional à função de onda naquele ponto (e à força do potencial da função delta).
Exemplos
Conjugado Hermitiano de um Operador Constante
Se temos o operador 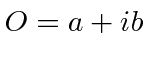 onde
onde ![]() e
e ![]() são reais, qual é o seu conjugado hermitiano? Pela definição do conjugado hermitiano
são reais, qual é o seu conjugado hermitiano? Pela definição do conjugado hermitiano
É fácil ver a partir da integral que
Portanto, o conjugado Hermitiano de um operador constante é seu conjugado complexo.
Conjugado Hermitiano de 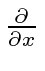
Queremos calcular o conjugado hermitiano do operador . Usaremos a integral para derivar o resultado. ![]()
Podemos integrar isso por partes, diferenciando ![]() e integrando para obter
e integrando para obter ![]() .
.
Portanto, o conjugado hermitiano de é . ![]()
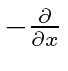
Observe que o conjugado Hermitiano do operador momentum é o mesmo do operador original. Portanto, o operador de impulso é Hermitiano. 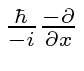
Problemas de teste de amostra
- Uma partícula está confinada a uma caixa de comprimento
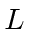 em uma dimensão. Ele está inicialmente no estado fundamental. De repente, uma parede da caixa é movida para fora, formando uma nova caixa de comprimento
em uma dimensão. Ele está inicialmente no estado fundamental. De repente, uma parede da caixa é movida para fora, formando uma nova caixa de comprimento 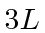 . Qual é a probabilidade de a partícula estar no estado fundamental da nova caixa? Você pode achar útil saber essa resposta
. Qual é a probabilidade de a partícula estar no estado fundamental da nova caixa? Você pode achar útil saber essa resposta 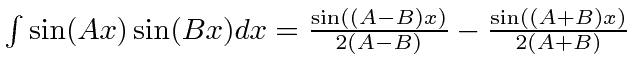
- Uma partícula de massa
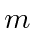 está em uma caixa unidimensional de comprimento L. A partícula está no estado fundamental. O tamanho da caixa é repentinamente (simetricamente) expandido para 3L de comprimento. Encontre a probabilidade de a partícula estar no estado fundamental do novo potencial. (Sua resposta pode incluir uma integral que você não precisa avaliar.) Encontre a probabilidade de estar no primeiro estado excitado do novo potencial.
está em uma caixa unidimensional de comprimento L. A partícula está no estado fundamental. O tamanho da caixa é repentinamente (simetricamente) expandido para 3L de comprimento. Encontre a probabilidade de a partícula estar no estado fundamental do novo potencial. (Sua resposta pode incluir uma integral que você não precisa avaliar.) Encontre a probabilidade de estar no primeiro estado excitado do novo potencial. - Duas autofunções degeneradas do hamiltoniano são normalizadas apropriadamente e possuem as seguintes propriedades.
Quais são os estados apropriadamente normalizados que são autofunções de H e P? Quais são suas energias? - Encontre os primeiros três (mais baixos) autoestados de energia para uma partícula localizada em uma caixa como essa
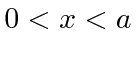 . Ou seja, o potencial é zero dentro da caixa e infinito fora. Estabeleça as condições de contorno e mostre que suas soluções as satisfazem. Normalize as soluções para representar uma partícula na caixa.
. Ou seja, o potencial é zero dentro da caixa e infinito fora. Estabeleça as condições de contorno e mostre que suas soluções as satisfazem. Normalize as soluções para representar uma partícula na caixa. - Uma partícula está no primeiro estado excitado de uma caixa de comprimento
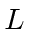 . Qual é esse estado? Agora, uma parede da caixa é repentinamente movida para fora para que a nova caixa tenha comprimento
. Qual é esse estado? Agora, uma parede da caixa é repentinamente movida para fora para que a nova caixa tenha comprimento 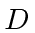 . Qual é a probabilidade de a partícula estar no estado fundamental da nova caixa? Qual é a probabilidade de a partícula estar no primeiro estado excitado da nova caixa?
. Qual é a probabilidade de a partícula estar no estado fundamental da nova caixa? Qual é a probabilidade de a partícula estar no primeiro estado excitado da nova caixa? - * Suponha isso. O que é? O que é? O que é?
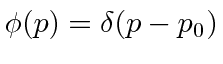
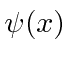
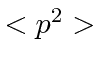
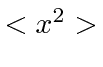
- Para uma partícula livre, o operador hamiltoniano H é dado por . Encontre as funções ,, que são autofunções tanto do hamiltoniano quanto de . Escreva a autofunção que tem autovalor de energia e autovalor de momento . Agora escreva as autofunções correspondentes no espaço de momento.
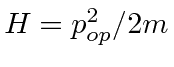
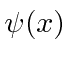
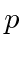
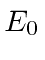
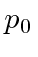
- * Uma partícula de massa
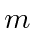 está em uma caixa unidimensional de comprimento L. A partícula está no estado fundamental. É feita uma medição do momento da partícula. Encontre a probabilidade de que o valor medido esteja entre
está em uma caixa unidimensional de comprimento L. A partícula está no estado fundamental. É feita uma medição do momento da partícula. Encontre a probabilidade de que o valor medido esteja entre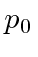 e
e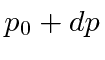 .
. - Uma partícula de massa
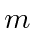 está em um potencial constante
está em um potencial constante 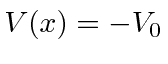 para todo x. Quais dois operadores comutam com o hamiltoniano e podem, portanto, se tornar constantes do movimento? Uma vez que esses dois operadores não comutam um com o outro, deve haver duas maneiras de escrever as autofunções de energia, uma correspondendo a cada operador de comutação. Escreva essas duas formas de autofunções do hamiltoniano que também são autofunções desses dois operadores.
para todo x. Quais dois operadores comutam com o hamiltoniano e podem, portanto, se tornar constantes do movimento? Uma vez que esses dois operadores não comutam um com o outro, deve haver duas maneiras de escrever as autofunções de energia, uma correspondendo a cada operador de comutação. Escreva essas duas formas de autofunções do hamiltoniano que também são autofunções desses dois operadores. - Uma partícula está confinada a uma "caixa" em uma dimensão. Ou seja, o potencial é zero para
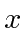 entre 0 e
entre 0 e 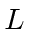 , e o potencial é infinito para
, e o potencial é infinito para 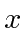 menos que zero ou
menos que zero ou 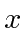 maior que
maior que 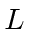 .
.
- a)
- Forneça uma expressão para as autofunções do operador hamiltoniano. Estas são as soluções independentes do tempo para este problema. (Dica: as funções reais serão mais simples de usar aqui.)
- b)
- Suponha que uma partícula esteja no estado fundamental desta caixa. Agora, uma parede da caixa é repentinamente movida de
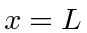 para
para 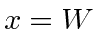 onde
onde 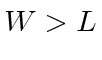 . Qual é a probabilidade de a partícula ser encontrada no estado fundamental do novo potencial? (Você pode deixar sua resposta no formulário que contém uma integral claramente especificada.)
. Qual é a probabilidade de a partícula ser encontrada no estado fundamental do novo potencial? (Você pode deixar sua resposta no formulário que contém uma integral claramente especificada.)
- Uma partícula de massa
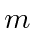 está em uma caixa unidimensional de comprimento
está em uma caixa unidimensional de comprimento 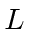 . A partícula está no estado fundamental. O tamanho da caixa é repentinamente expandido para o comprimento
. A partícula está no estado fundamental. O tamanho da caixa é repentinamente expandido para o comprimento 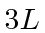 . Encontre a probabilidade de a partícula estar no estado fundamental do novo potencial. (Sua resposta pode incluir uma integral que você não precisa avaliar.) Encontre a probabilidade de estar no primeiro estado excitado do novo potencial.
. Encontre a probabilidade de a partícula estar no estado fundamental do novo potencial. (Sua resposta pode incluir uma integral que você não precisa avaliar.) Encontre a probabilidade de estar no primeiro estado excitado do novo potencial.
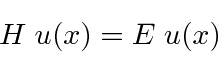
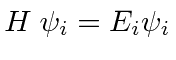
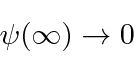
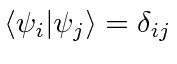
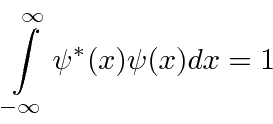
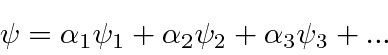
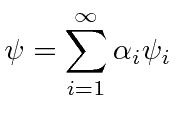
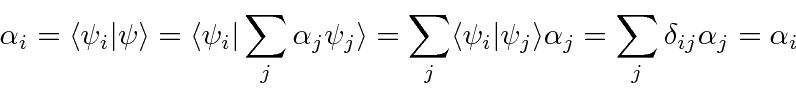
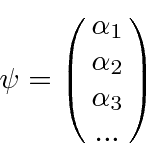
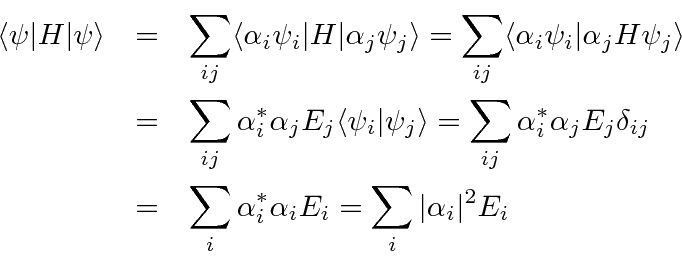
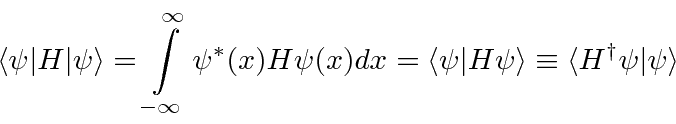
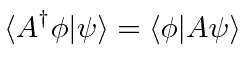
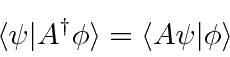
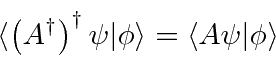
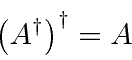
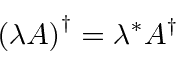
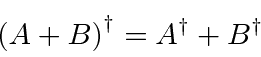
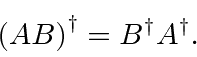
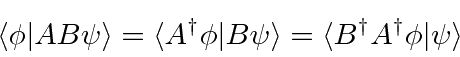
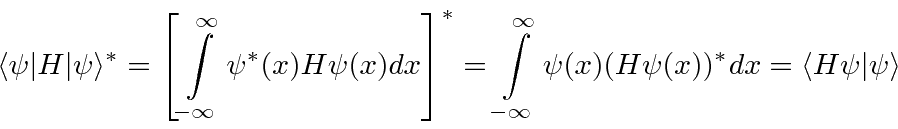
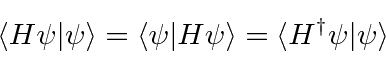
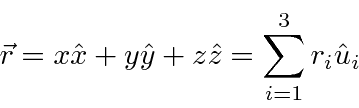
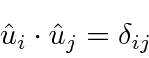
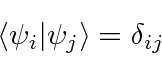
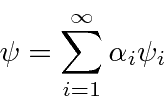
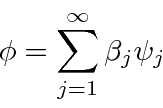
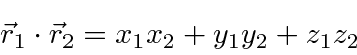
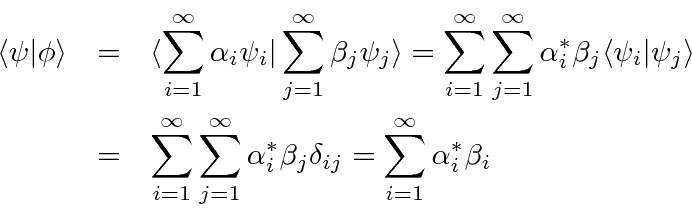
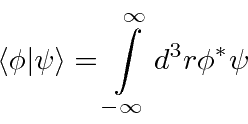
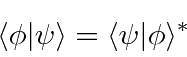
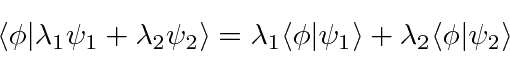
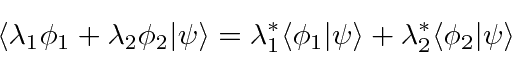
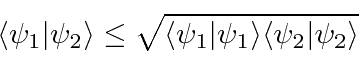
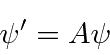
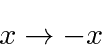
![\ begin {displaymath} \ bgroup \ color {black} [H, P] = 0 \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1158.png)
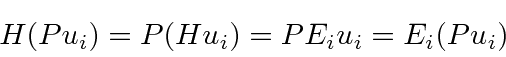
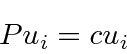
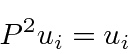
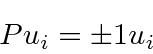
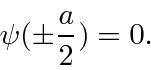
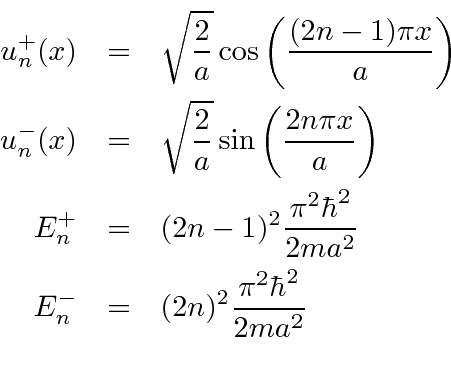
![\ begin {displaymath} \ bgroup \ color {black} \ psi (x) = \ sum \ limits_ {n = 1} ^ \ infty [A_n ^ + u_n ^ + (x) + A_n ^ -u_n ^ - (x) ] \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1169.png)
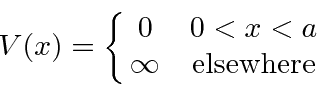
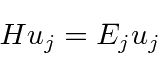
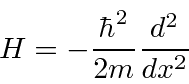
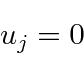
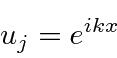
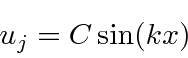
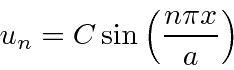
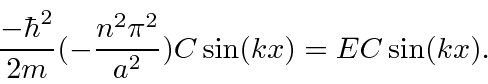
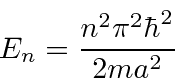
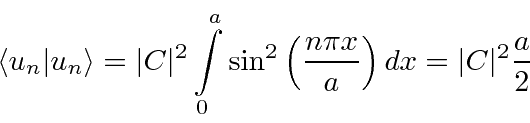
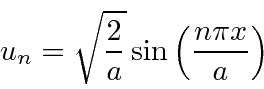
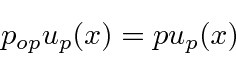
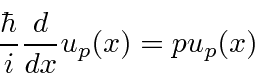
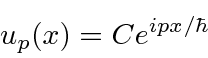
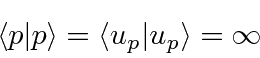
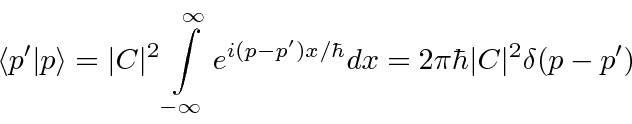
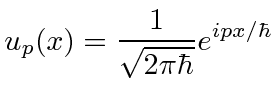
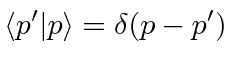
![\ begin {eqnarray *} [H, p] = 0 \\ {[H, P] = 0} \\ \ end {eqnarray *}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1177.png)
![\ begin {displaymath} \ bgroup \ color {black} [P, p] \ neq 0. \ egroup \ end {displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1178.png)