MATLAB é uma linguagem matemática, especialista na realização de cálculos e manipulações matemáticas, bastante ampla em suas funcionalidades, permitindo a apresentação dos resultados em gráficos em duas e três dimensões.
A linguagem trabalha com valores numéricos inteiros, reais e complexos, strings (cadeias de caracteres), booleanos (valores lógicos true ou false, 1 ou 0), etc.
Escalares são valores unitários dos tipos citados acima.
Entretanto no MATLAB os elementos compõe sempre uma matriz de uma ou mais dimensões.
Mesmo um simples escalar compõe uma matriz 1×1.
Daí o nome MATLAB = MATrix LABoratory.
Esse enfoque, aliado a um grande repertório de formas, funções e ’toolboxes’ para criação, manipulação e operações com matrizes, compõem um sistema que permite a programação e resolução de muitos problemas numéricos em apenas uma fração do tempo que se gastaria para escrever um programa semelhante em outras linguagens de uso geral, como por exemplo, Javascript, Fortran, Basic ou C.
O MATLAB permite a manipulação simbólica de variáveis, usando uma caixa de ferramentas - toolbox - específica para isso.
A conjugação da manipulação simbólica com a facilidade de manipulação de matrizes torna fácil o trabalho com álgebra matricial, por exemplo.
Os resultados dos cálculos e manipulações numéricas podem ser apresentados de forma textual ou gráfica.
O aplicativo que deu origem à linguagem é o homônimo MatLab, software proprietário que tem similar open-source - aberto e livre de pagamento de licença - no Octave.
O Octave incorpora a linguagem MATLAB com grande compatibilidade de recursos matemáticos e gráficos com o MatLab, desde a GUI de trabalho até a interpretação da linguagem MATLAB.
Está disponível para todos os principais sistemas operacionais (Windows, MacOS, Linux) e também na internet (www.octave-online.net).
Comandos, operações e funções
A MATLAB tem muitos recursos matemáticos para realização de operações aritméticas, algébricas, trigonométricas, logarítmicas, entre outras, além de diversas funções, operando através do uso de matrizes e as plotando em gráficos variados 2D e 3D.
Operadores de concatenação de matrizes
As matrizes operadas pela MATLAB são criadas através da concatenação de valores em linhas e colunas, utilizando-se os operadores de concatenação "[ ]" iniciando e finalizando a concatenação e os operadores de separação espaço " " e virgula "," para separar colunas, e o símbolo ponto-e-vírgula ";" separando as linhas nas matrizes.
Operadores aritméticos
As operações aritméticas são a soma, subtração, multiplicação e divisão.
Os símbolos correspondentes no MATLAB são "+", "-", "*" e "/" ou "\", respectivamente.
Operadores algébricos
As expressões algébricas são as equações com uma ou mais incógnitas, elevadas a alguma potencia nas equações de segundo grau e diante.
A potenciação na MATLAB utiliza o símbolo circunflexo "^" para elevar um valor à potencia de outro.
Comandos e operadores lógicos
A MATLAB permite blocos condicionais de comandos com a as palavras reservadas if, else e elseif, utilizando os operadores condicionais igual "==", diferente "~=", maior ">", maior ou igual ">=", menor "<", menor ou igual, "<=".
Comandos de repetição
Os comandos de repetição for e while executam blocos de comandos até a condição de término ser verdadeira.
Gráficos 2D e 3D
A MATLAB produz muitos tipos de gráficos 2D e 3D.
| Linha | Dispersão e bolha | Distribuição de dados | Dados discretos | Geográficos | Polar | Contorno | Vetoriais | Superfície e malha | Visualização de volume | Animação | Images |
|---|---|---|---|---|---|---|---|---|---|---|---|
Visão geral do curso
- Familiarização com a linguagem MATLAB e o ambiente do Octave: descrição das características básicas da linguagem e demos.
- Detalhamento dos aspectos mais importantes da linguagem.
- Apresentação das operações algébricas, lógicas e das funções específicas do MATLAB.
- Exemplos, muitos exemplos o tempo todo.
A linguagem MATLAB (MATrix LABoratory) teve origem com o software MatLab, que deu nome à linguagem e definiu-lhe as funcionalidades.
O MatLab trata-se de um software interativo de alta performance voltado para o processamento matemático, com manipulações e cálculos numéricos, integrando - através da interpretação de instruções da linguagem MATLAB - análise numérica, cálculo com matrizes, processamento de sinais e construção de gráficos, em ambiente gráfico de fácil utilização onde os problemas e soluções são expressos como são escritos matematicamente, ao contrário da programação tradicional.
Entretanto, o MatLab tem licenciamento pago. Muitos softwares proprietários com licença paga têm um ou mais similar, desenvolvido de forma aberta por uma comunidade ativa, tornando-se propriedade de todos - mesmo quem não participou do desenvolvimento, livre de encargos. Uma comunidade interessada que, em grupo, muitas vezes consegue resultados mais expressivos que o software original, proprietário, uma vez que não existem limites para participação de voluntário em projetos open-source, enquanto que sistemas proprietários de empresas privadas necessitam investimento constante, contratação de mão-de-obra, etc.
Similar ao MatLab temos - e utilizaremos - o Octave, software open-source , de código aberto e disponível a quem possa interessar, livre de licença para instalação em diferentes sistemas operacionais (Windows, MacOS e Linux), altamente compatível com a linguagem MATLAB.
Utilizaremos o Octave em nossos exemplos.
Mostraremos como pode ser baixado no site da comunidade GNU (GNU’s Not Unix), instalado e utilizado.
Temos também a versão do Octave Online, uma GUI (Graphical User Interface, interface gráfica de usuário) interativa, ótima para execução de instruções cuja complexidade não impliquem no consumo excessivo de memória e de tempo. Para nossos propósitos didáticos o Octave Online é excelente, atende muito bem.
Então, neste curso, quando nos referirmos à MATLAB - em caixa alta - estaremos nos referindo à linguagem. Linguagem é dialeto, então tanto faz MATLAB ser referida como "a (linguagem) MATLAB "ou referido como "o (dialeto) MATLAB.", mas iremos normalmente nos referir como "a (linguagem) MATLAB". Nos referindo a MatLab - em caixa baixa - estaremos nos referindo ao aplicativo proprietário, o que será raro, pois todo nosso trabalho será desenvolvido com o Octave.
Quando nos referirmos a Octave - em caixa baixa - estaremos nos referindo ao aplicativo na versão Windows ou na versão online da internet.
A linguagem do Octave é o OCTAVE, compatível com o MATLAB, mas com pequenas mudanças que podem ocorrer. Assim sendo, o aplicativo Octave tem sua própria linguagem praticamente semelhante ao MATLAB, chamada OCTAVE mesmo, em caixa alta para diferenciar a linguagem do aplicativo Octave.
Entretanto para efeito didático consideraremos estar utilizando a linguagem MATLAB mesmo - mais conhecida, mais popular, - e não o dialeto OCTAVE. - que é praticamente o MATLAB.
Então, OCTAVE é uma linguagem computacional que possui alta compatibilidade com MATLAB, possuindo um grande número de operações e funções semelhantes. desenvolvida para computação matemática como a linguagem nativa do aplicativo Octave, mas que não será referida aqui, apenas a MATLAB, salvo caso específico, se necessário.
O aplicativo para Windows (ou melhor, para o sistema operacional de seu computador, utilizamos Windows), pode ser baixado, instalado e rodar no sistema operacional, onde as operações matemáticas poderão ser declaradas, processadas, calculadas, manipuladas e os resultados textuais e gráficos apresentados nas GUI de apresentação disponíveis para isso.
O aplicativo Octave possui funcionamento parecido com o do aplicativo MatLab, disponibilizando uma interface para entrada de linhas de comando com instruções para a solução de problemas numéricos, lineares e não-lineares, experimentos numéricos e produção de gráficos.
Octave foi escrito por John W. Eaton, faz parte do projeto GNU, é um software livre sob os termos da licença GPL, e roda no seu ambiente de trabalho a linguagem MATLAB.
Algumas produções gráficas utilizando-se MATLAB:
Octave é o software open-source com licença de uso livre de pagamento, similar ao MatLab, software homônimo da linguagem MATLAB e que deu origem à linguagem, que porém é produto proprietário que exige pagamento de taxa para licenciamento de uso.
Apresentamos no tópico anterior o Octave Online, versão na internet do Octave, que pode ser utilizado sem a necessidade de instalação do aplicativo no computador, porém tem limitação de memória e tempo, mesmo asssim funciona muito bem.
Existe a versão desktop para instalação em computadores pessoais para diferentes sistemas operacionais: Windows, MacOS, Linux.
Iremos agora apresentar como baixar, instalar e rodar o Octave Desktop no Windows, sistema operacional que utilizamos na RPT Lab
Para instalarmos o Octave, pesquisamos ''octave download" com algum mecanismo de busca, tipo o Google.
Selecionamos na pesquisa retornada o link de download do Octave, certamente será apresentado.
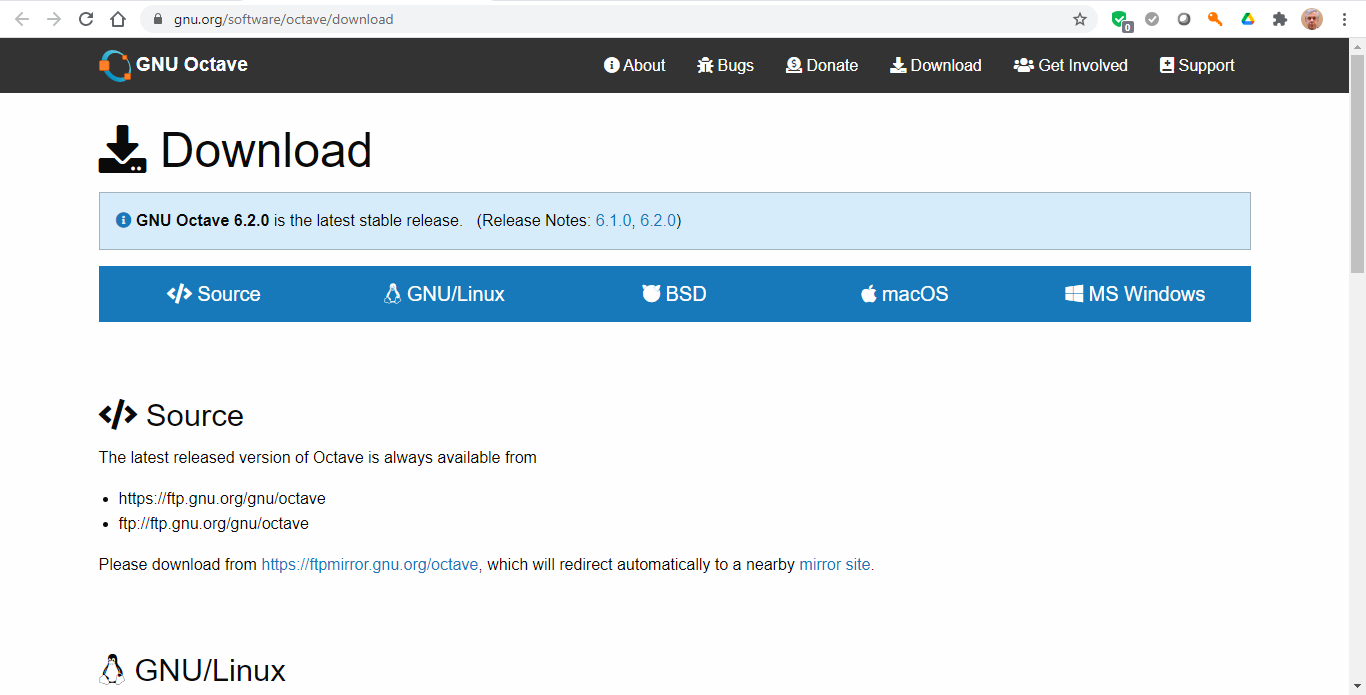
Clicamos em MS Windows na tela de download do Octave.
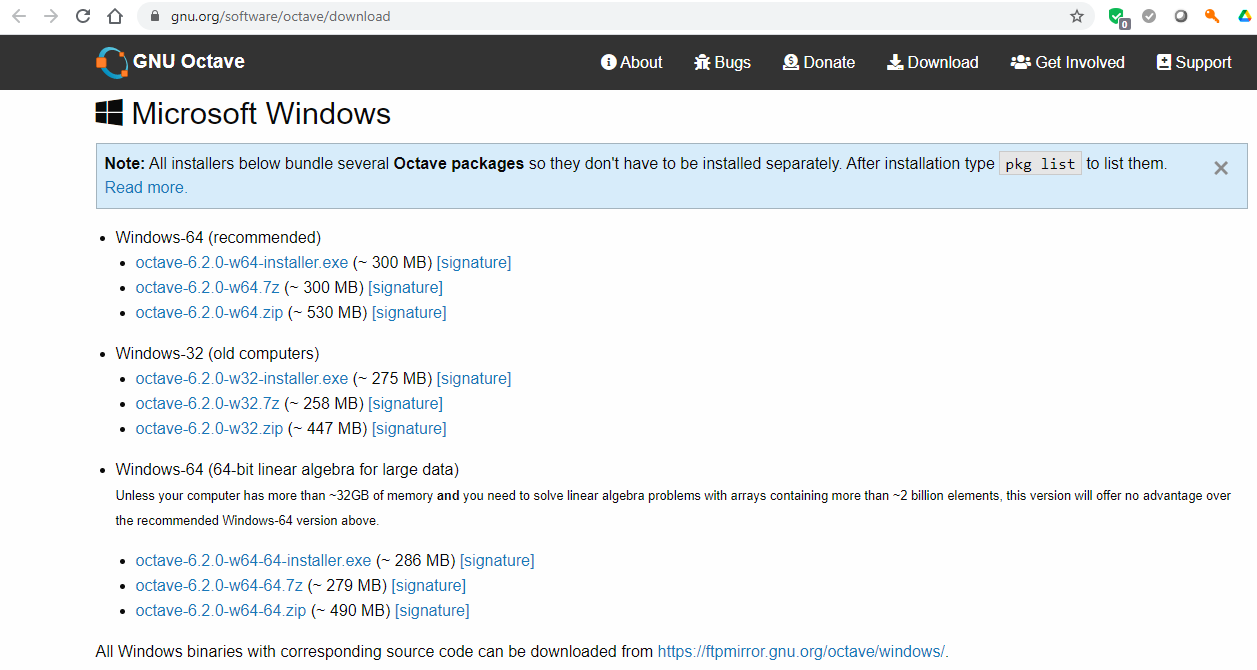
Selecionamos a opção desejada, dependendo do Windows ser de 64 ou 32 bits.
Nesta instalação selecionamos octave-6.2.0-w64-installer.exe. Os computadores da RPT LABS são de 64 bits com Windows 64 bits, então usamos tudo 64 bits, estando disponível a versão compatível.
O download será iniciado.
Após o programa instalador do Octave ser "baixado" exploramos o diretório de downloads para localizar o programa instalador.
Uma vez localizado clicamos no ícone do programa instalador para iniciar a instalação do Octave.
Conferimos a licença (em inglês, mas livre, podemos aceitar tranquilamente) e clicamos em next.
Selecionamos o tipo de instalação e clicamos em next.
Selecionamos as opções de instalação desejadas e clicamos em next.
Selecionamos o local de instalação e clicamos em next.
E a instalação será iniciada.
Após a instalação ser concluída clicamos no botão Finish para encerrar.
 Desinstalação do Octave para Windows
Desinstalação do Octave para Windows
Eventualmente precisaremos ou desejaremos desinstalar o Octave do Windows.
Vamos ao painel de controle --> programas padrão --> definir os programas padrão --> aplicativos e recursos (com o Windows em português).
Clicando em Desinstalar é iniciada a remoção do Octave.
Talvez nos seja solicitado ordenarmos a remoção dos diretórios porventura usados durante o tempo de utilização do Octave. Clicamos em sim para continuar.
Realizada a desinstalação do Octave, clicamos em finish para encerrar.
Observe que Octave não aparece mais no painel de aplicativos e recursos.
Quando o aplicativo MatLab foi criado, no final da década de 1970, os recursos computacionais eram escassos, por isso muitos aplicativos para Windows têm ainda um jeitão antigo daquela época, como o MatLab.
Entretanto as coisas mudaram muito de lá para cá e temos hoje, inclusive, a internet que oferece inúmeros recursos avançados, disponíveis online para os usuários, desde que estejam conectados.
Um recurso mais que bacana é o Octave Online, que nos permite - com algumas limitações de memória e tempo na realização de operações matemáticas - utilizarmos o Octave direto no nosso navegador-web , sem a necessidade de ser instalado no computador ou celular.
Após acessado no endereço https://octave-online.net é apresentada a janela de boas-vindas do Octave Online.
O Octave Online está em inglês mas isto não será grande problema para aqueles sem o domínio do idioma, pois a sua utilização é bastante simples e direta, enquanto produzindo resultados matemáticos complexos. Opcionalmente está disponível o idioma espanhol.
Nos interessa basicamente a digitação de instruções para realização de operações matemáticas e apresentação de gráficos.
Clicamos no botão Start Using Octave Online para iniciar o uso do Octave Online.
 Fechamos as janelas de dicas clicando em "dismiss", A dica "Octave Command Prompt" indica o local para entrada de comandos, chamado prompt.
Fechamos as janelas de dicas clicando em "dismiss", A dica "Octave Command Prompt" indica o local para entrada de comandos, chamado prompt.
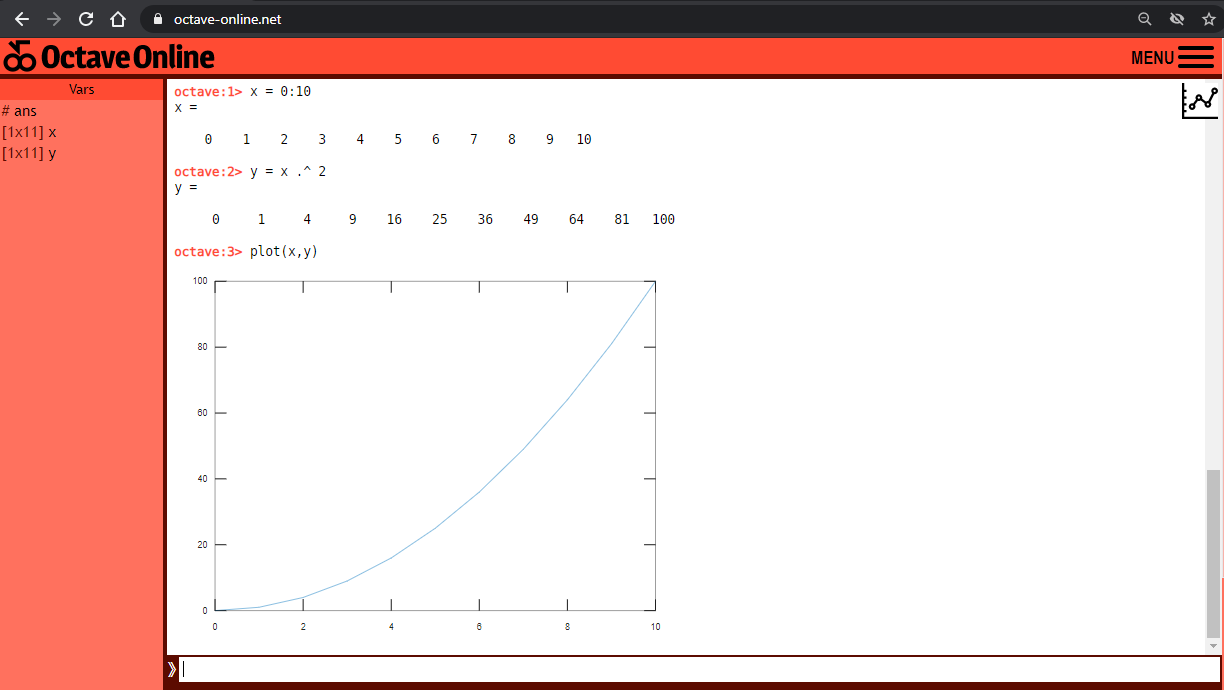
Digitamos nossas instruções na linha de comandos (prompt).
A MATLAB é especializada na operação com vetores e matrizes, os quais podemos declarar e apresentar em gráficos, facilmente.
Iremos ao longo do curso detalhar as declarações, instruções, comandos, funções, argumentos das funções, escalares, matrizes, etc.
Mas para um início rápido vamos declarar dois vetores x e y e criar o gráfico correspondente.
O vetor x conterá sequência de escalares de 0 a 10.
O vetor y conterá a sequência, nas posições correspondentes, com os valores dos elementos de x elevados a 2.
A função plot plota o gráfico de x x y.
>> x = 0:10
x = 0 1 2 3 4 5 6 7 8 9 10
>> y = x .* 2
y = 0 1 4 9 16 25 36 49 64 81 100
>> plot(x,y)
O plano cartesiano é formado pelos eixos, duas retas reais perpendiculares, ou seja, com ângulo de 90° entre elas, sendo a reta horizontal é o eixo das abscissas e a reta vertical é o eixo das ordenadas.
MATLAB é muito fácil de usar, e muito fácil para praticarmos matemática.
Podemos reaproveitar variáveis e vamos agora atribuir a y (do exemplo anterior) o vetor com a sequência com os valores dos elementos de x nas mesmas posições.
>> y = x
x = 0 1 2 3 4 5 6 7 8 9 10
>> plot(x,y)
A linguagem MATLAB permite a criação de matrizes e a solução de expressões aritméticas, equações algébricas, funções trigonométricas, utilizando variáveis, blocos condicionais e de repetição, dentre muitos recursos disponíveis.
O recurso mais básico da MATLAB são as operações aritméticas com escalares, como a simples soma de 2 + 2.
>> 2 + 2
ans = 4
Matemática simples: Joaquim vai à papelaria e compra 4 borrachas por 25 centavos cada, 6 blocos por 52 centavos cada e 2 fitas adesivas por 99 centavos cada. Quantos itens comprou e quanto gastou?
Usamos a calculadora para calcular o total de itens, o preço total em centavos e o preço total em reais.
4 + 6 + 2 = 12 (itens)
4 x 25 + 6 x 52 + 2 x 99 = 610 (centavos)
610 / 100 = 6,10 (reais)
Usando MATLAB comandamos as operações aritméticas básicas de forma similar à calculadora.
>> 4 + 4 + 2
ans = 12
>> 4 * 25 + 6 * 52 + 2 * 99
ans = 610
>> 610 / 100
ans = 6.10
Obs: ans = answer = resposta
Operações aritméticas básicas
As operações aritméticas básicas são: soma, subtração, multiplicação e divisão.
A operação entre escalares utilizam os símbolos mais "+", menos "-", asterisco "*" e divisão "/".
>> 6 + 2 % Soma
ans = 8
>> 6 - 2 % Subtração
ans = 4
>> 6 * 2 % Multiplicação
ans = 12
>> 6 / 2 % Divisão
ans = 3Escalares, Vetores e Matrizes
Para a MATLAB todas as variáveis são matrizes.
Chamamos escalares aqueles valores unitários de diferentes tipos: numéricos inteiros e reais, strings (cadeias de caracteres), booleanos (valores lógicos true-false ou 1-0).
Mas mesmo valores escalares na MATLAB são tratadas como matrizes 1x1, com uma linha e uma coluna. Estes vetores com 1x1 serão referidos como vetores unitários.
Vetores são matrizes unidimensionais com uma linha ou uma coluna. Normalmente o termo vetor com matrizes de ordem 1xn ou nx1 com n > 1.
Matrizes são composições de elementos em linhas em colunas, de ordem mxn, com m> 1 e n > 1.
Criação de matrizes
Matrizes são criadas com valores entre colchetes "[ ]" separados por espaço " " ou vírgula, para separar colunas, ou ponto-e-vírgula ";" para separar linhas.
>> [1 2 3 ; 4 5 6 ; 7 8 9 ]
ans =
1 2 3
4 5 6
7 8 9
Variáveis
Podemos atribuir a variáveis os resultados das operações que realizamos.
Variáveis "recebem" valores. Na verdade apontam para valores alocados e armazenados na memória após uma operação qualquer, mas no popular dizemos "que as variáveis recebem valores".
Evoluindo o exemplo de que Joaquim vai à papelaria e compra 4 borrachas a 25 centavos cada, 6 blocos a 52 centavos cada e 2 fitas adesivas a 99 centavos cada, usando variáveis nas operações, calculamos quantos itens comprou e quanto gastou.
>> borrachas = 4
borrachas = 4
>> blocos = 6
blocos = 6
>> fitas = 2
fitas = 2
>> items = borrachas + blocos + fitas
items = 12
>> custo_centavos = borrachas * 25 + blocos * 52 + blocos * 99
custo_centavos = 610
>> custo_reais = borrachas * .25 + blocos * .52 + blocos * .99
custo_reais = 6.10
% ou
>> custo_reais = custo_centavos / 100
custo_reais = 6.10Observe acima que em valores reais v onde -1 < v < 1 o zero pode ser suprimido à esquerda do ponto decimal.
Variáveis especiais
O MATLAB tem algumas variáveis especiais que podemos utilizar em nossas operações. Abaixo temos alguns exemplos:
pi % a constante PI.
beep % faz o computador soar um beep.
i ou j % sqrt(-1)
inf % infinito
realmin % Menor real positivo que pode ser usado.
realmax % Maior real positivo que pode ser usado.
bitmax % Maior inteiro positivo que pode ser usado.
Variáveis especiais podem ter seus valores alterados.
>> pi % ans = 3.1416
>> pi = 233e3 % pi = 233000
>> clear pi >> pi % ans = 3.1416
Variáveis criadas pelo usuário são incorporadas ao workspace da MATLAB .
Liberação de variáveis
A função clear <var> remove a variável <var> do workspace , sendo uma variável por nós definida pelo usuário, ou reestabelece o seu valor original sendo uma variável especial.
O comando var ou var = all , remove todas as variáveis definidas pelo usuário e restabelece os valores iniciais das variáveis especiais.
Reutilização de variáveis
O MATLAB permite uma variável já declarada receber novo valor:
>> x = 10;
x = 10
>> x = 20
x = 20
Isto colabora para que, em muitas situações, o gerenciamento da memória seja otimizado proporcionando a liberação de dados intermediários das operações.
A reutilização das variáveis não afeta cálculos anteriores.
>> borrachas = 4
borrachas = 4
>> blocos = 6
blocos = 6
>> fitas = 2
fitas = 2
>> items = borrachas + blocos + fitas
items = 12
>> borrachas = 8
borrachas = 8
>> blocos = 7
blocos = 7
>> fitas = 4
fitas = 4
>> items
items = 12
Palavras reservadas
O MATLAB tem palavras reservadas que não devemos usar como nomes de variáveis para não causarmos erros de interpretação dos comandos MATLAB.
As principais palavras reservadas são:
for end while function return try
if elseif else case continue switch
catch global persistent break otherwisePontuações especiais no MATLAB
Comentários: O símbolo % instrui ao interpretador MATLAB para que ignore o texto que o segue.
>> pi % exibe o valor da constante pi ans = 3.1416Múltiplos comandos na mesma linha: Os comandos devem ser separados por vírgula ou ponto-e-vírgula.
>> borrachas = 4, blocos = 6; borrachas + blocos % erasers = 4, ans = 10Quebra de linha
O símbolo três-pontos "..." no final da linha indica ao interpretador que a operação do comando continuará na linha seguinte.
>> a = 10; b = 20; c = 30; % finalizados com ";" não mostram o resultado na JC
>> items = a + ... % O comando inicia e continua ...
>> b +... % e continua ...
>> c % e encerra.
items = 60Aritmética de ponto flutuante
Os números são representados em aritmética de precisão dupla, usando código binário na representação interna.
- Nem todos os números podem ser representados exatamente.
- Existem limites para os valores poderem ser representados.
- Existe um valor-limite inferior que efetivamente pode ser somado a um número de forma a mudar seu valor.
>> format long % exibe mais dígitos
>> eps % menor num. que somado a 1 gera num > 1
ans = 2.220446049250313e-16
Comutatividade da adição: nem sempre vale!
>> 0.42 - 0.5 + 0.08
ans = -1.387778780781446e-17
>> 0.08 - 0.5 + 0.42
ans = 0
>> 0.08 + 0.42 - 0.5
ans = 0
Argumentos e valores de funções nem sempre precisos!
>> sin(0)
ans = 0
>> sin(pi)
ans = 1.224646799147353e-16Configuração de formatação numérica
O formato numérico exibido na tela pode ser modificado utilizando-se o comando format, que afeta somente o modo como as matrizes são mostradas, e não como elas são computadas ou salvas (a MATLAB efetua todas operações em dupla precisão).
O formato numérico depende do tipo,
Depende do tipo do número, inteiros são exibidos sem casas decimais e são exibidos com 4 dígitos após a vírgula.
Com números reais se os dígitos significativos estiverem fora do intervalo de 4 dígitos após a vírgula o resultado será exibido em notação científica (como calculadoras).
A tabela a seguir apresenta os comandos para formatação numérica:
| comando | Exemplo |
| format short | 3.1416 (5 dígitos) |
| format short e | 3.1416e+00 (5 dígitos mais expoente) |
| format short g | 3.1416 (melhor entre opções short) |
| format long | 3.14159265358979 (16 dígitos) |
| format long e | 3.14159265358979e+00 (16 dígitos mais expoente) |
| format long g | 3.14159265358979 (melhor entre opções long) |
| format hex | 400921fb54442d18 (hexadecimal com ponto flutuante) |
| format bank | 3.14 (2 dígitos) |
| format + | + (positivo(+), negativo(-) ou zero(0)) |
| format rat | 355/113 (aproximação racional) |