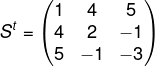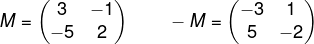Funções com matrizes

Existem muitas funções para criação, manipulações e consulta de matrizes.

Funções de Concatenação

Adiante apresentaremos diversas funções para concatenação de matrizes, entretanto nesse momento daremos importância para algumas funções a apresentar algumas bastante importantes, por serem muito utiizadas, para a criação de matrizers.

linspace

A função linspace(vinicial,vfinal,n) retorna um vetor com n elementos, sendo  o primeiro = vinicial  e o último = vfinal.

Suponhamos calcular o seno de x para k valores de x uniformemente distribuídos entre [0, π].

Podemos criar usando cochetes, atribuindo k =  200 e n = 1.

>> k=200,n=1
k = 200
n = 1

>> variacao = n/k
ans = 5.0000e-03

>> A = 0:variacao:1
A = 
    Columns 1 through 6:
    0 0.005 0.010 0.015 0.020 0.025 0.030 0.035 0.040 0.045 0.050 0.055 0.060
    ...
    Columns 196 through 201:
    0.975 0.980 0.985 0.990 0.995 1.000

>> size(A)
ans = 201

Observamos que A ficou com  201 elementos, um a mais do que o especificado na variável k.

Isso porque para termos k elementos precisamos no cálculo da variação subtrair 1 de seu valor antes da divisão de n por este valor.

>> variação = n / ( k - 1 )
ans = 5.0251e-03

>> A = 0:variacao:1
A = 
    Columns 1 through 6:
    0 0.0050 0.0101 0.0151 0.0201 0.0251
    ...
    Columns 196 through 200:
    0.9799 0.9849 0.9899 0.9950 1.0000

>> size(A)
ans = 200

 

É necessário que haja uma forma mais automática de inserir valores em um vetor para que possamos cumprir este objetivo de forma eficiente.

>> x = linspace(0,pi,200)
x = Columns 1 through 7
0 0.0158 0.0316 0.0474 0.0631 0.0789 0.0947
Columns 8 through 14
0.1105 0.1263 0.1421 0.1579 0.1737 0.1894 0.2052
Columns 15 through 21
0.2210 0.2368 0.2526 0.2684 0.2842 0.3000 0.3157
...
Columns 190 through 200
2.9837 2.9995 3.0153 3.0311 3.0469 3.0627 3.0784 3.0942 3.1100 3.1258 3.1416

logspace

>> x = logspace(<pot_ini>,<pot_fim>,<num_ele>)

Cria um vetor com num_ele elementos logaritmicamente espaçados, cujo primeiro elemento é 10pot_ini e o último elemento é 10pot_fim.

Números e matrizes associadas a A

Seja A uma matriz com dimensão qualquer temos números e matrizes associados que são obtidos através de funções.

Nos exemplos a seguir utilizaremos as matrizes A e R, sendo A uma matriz de ordem 1x8 e R uma matriz de ordem 2x4.

>> A = 1:8
A = 1 2 3 4 5 6 7 8
>> size(A)
ans = 8

>> R = [ 1:4 ; 5:8 ]
R = 
    1 2 3 4
    5 6 7 8

size

O comando size(A) retorna a(s) dimensão(ões) da matriz A, que pode ser um escalar, um vetor ou uma matriz.

size(A) é o par de números [m n].

>> size(A)
ans = 8

>> size(R)
ans = 2 4

>> [r,c] = size(R)
r = 2
c = 4

>> size(R,1) 
ans = 2

>> size(R,2)
ans = 4

numel

A função numel(A) retorna o número de elementos de A.

>> numel(A)
ans = 8

>> numel(R)
ans = 8

length

A função length(A) Retorna o tamanho da maior dimensão de A.

>> length(A)
ans = 8

>> length(A)
ans = 4

Se for um vetor unidimensional o resultado é o mesmo retornado por size(A).

ndims

A função ndims(A) retorna o número de dimensões do vetor A.

Esta função é equivalente a length(size(A)).

>> ndims(A) % Ordem mxn: 1x8 - 2 dimensões
ans = 2

>> ndims(A) % Ordem mxn: 2x4 - 2 dimensões
ans = 2

rank

A função rank (A) retorna o posto (número de pivôs, igual a dimensão do espaço da linha e do espaço da coluna).

>> rank(A) % Ordem mxn, m=1, 1 pivô
ans = 1

>> rank(R) % Ordem mxn, m=2, 2 pivôs
ans = 2

trace

A função trace(A) retorna traço (= soma das entradas diagonais = soma dos autovalores)

>> trace(A)
ans = 1

>> rank(R)
ans = 7

null

a função null(A) é a matriz cujas colunas n - r são uma base ortogonal para o espaço nulo de A

>> null(A)
ans =
  -0.140028  -0.210042  -0.280056  -0.350070  -0.420084  -0.490098  -0.560112
   0.981675  -0.027487  -0.036650  -0.045812  -0.054975  -0.064137  -0.073299
  -0.027487   0.958769  -0.054975  -0.068718  -0.082462  -0.096205  -0.109949
  -0.036650  -0.054975   0.926701  -0.091624  -0.109949  -0.128274  -0.146599
  -0.045812  -0.068718  -0.091624   0.885470  -0.137436  -0.160342  -0.183248
  -0.054975  -0.082462  -0.109949  -0.137436   0.835076  -0.192411  -0.219898
  -0.064137  -0.096205  -0.128274  -0.160342  -0.192411   0.775521  -0.256548
  -0.073299  -0.109949  -0.146599  -0.183248  -0.219898  -0.256548   0.706802

>> null(R)
ans =
  -0.400087  -0.374072
   0.254633   0.796971
   0.690996  -0.471724
  -0.545542   0.048826

orth

A função orth(A) retorna a matriz cujas colunas são a base ortogonal para o espaço de coluna de A.

>> ortho(A)
ans = -1

>> ortho(R)
ans =
     0.3762  0.9266
     0.9266 -0.3762

Matrizes especiais

Podem ter um ou dois parâmetros: com um parâmetro gera uma matriz quadrada; com dois parâmetros, m,n, gera uma matriz de ordem m×n.

ones

A função ones(n) retorna uma matriz com n elementos com o valor escalar 1, sendo arg um escalar, um vetor ou uma matriz.

% ones(n) Retorna matrizes quadradas de ordem n preenchidas com 1

>> A = ones(1)
A = 1

>> A = ones(2)
A =
    1 1
    1 1

>> A = ones(3)
A =
    1 1 1
    1 1 1
    1 1 1

% assim por diante

A função ones(m,n) retorna uma matriz de ordem mxn elementos com o valor escalar 1.

% ones(m,n) Retorna matrizes de ordem mxn preenchidas com 1

>> A = ones(1,2)
A = 1 2

>> A = ones(2,1)
A =
    1
    1

>> A = ones(2,3)
A =
    1 1 1
    1 1 1

>> A = ones(3,2)
A =
    1 1
    1 1
    1 1

% assim por diante

zeros

A função zeros(n) e zeros(m,n) retorna matrizes com n elementos ou mxn elementos com o valor escalar 1.

toeplitz

A função toeplitz(A) fornece a matriz diagonal-constante de Toeplitz simétrica, usando as primeiras linha e coluna de A, onde:

  • Se A for um vetor real, então rdefine a primeira linha da matriz.
  • Se A for um vetor complexo com um primeiro elemento real, então redefine a primeira linha e redefine a primeira coluna.
  • Se o primeiro elemento de r for complexo, a matriz de Toeplitz é Hermitiana fora da diagonal principal, o que significa Teu,j= conj(Tj,eu) para i ≠ j. Os elementos da diagonal principal são definidos como r(1).
>> toeplitz(A)
ans =
   1   2   3   4   5   6   7   8
   2   1   2   3   4   5   6   7
   3   2   1   2   3   4   5   6
   4   3   2   1   2   3   4   5
   5   4   3   2   1   2   3   4
   6   5   4   3   2   1   2   3
   7   6   5   4   3   2   1   2
   8   7   6   5   4   3   2   1

toeplitz(A,v) fornece a matriz de Toeplitz com diagonal-constante não-simétrica, usando as primeiras linha e coluna de A.

Se os primeiros elementos de A forem diferentes, a função emite um aviso e usa o elemento de coluna para a diagonal. 

>> toeplitz(1,A)
ans = 1 2 3 4 5 6 7 8

>> toeplitz(2,A)
ans = 2 2 3 4 5 6 7 8

>> toeplitz(3,A)
ans = 3 2 3 4 5 6 7 8

eye

A função eye(n) fornece matriz identidade com ordem mxn com m = n. Veremos sobre a matriz identidade abaixo.

rand

rand(n) fornece matriz n x n com entradas aleatórias entre 0 e 1 (distribuição uniforme)

rand(arg)

Retorna uma matriz com elementos aleatórios uniformemente distribuídos no intervalo [0..1].

randn(n) fornece matriz n x n com entradas normalmente distribuídas (média 0 e variância 1)

diag

A função diag(vetor <,pos>) retorna uma matriz com elementos em uma diagonal paralela à diagonal principal.

A diagonal paralela é determinada pelo parâmetro opcional pos, que não sendo declarado assume 0.

>> v = 1:2
v = 1 2
>> d1 = diag(a)
d1 =
    1 0
    0 2

>> d2 = diag(a,1)
d2 =
    0 1 0
    0 0 2
    0 0 0

>> diag(a,-1)
d3 =
    0 0 0
    1 0 0
    0 2 0

Com o comando diag(vetor <,pos>), com a variável vetor já sendo existente, faz com que a função diag retorne a sua matriz diagonal, de acordo com os argumentos da função. O argumento pos possui a mesma função do caso anterior.

>> a = [1,2,3;4,5,6;7,8,9]
a =
    1 2 3
    4 5 6
    7 8 9
>> d1 = diag(a)
d1 =
    1
    5
    9
>> d2 = diag(a,1)
d2 =
    2
    6
>> d3 = diag(a,-1)
d3 =
    4
    8

Mais exemplos:

>> A = [1,2,3;4,5,6]
A =
    1 2 3
    4 5 6

>> B = A(end:-1:1,:)
B =
    4 5 6
    1 2 3

>> C = [A B(:,[1 3])]
C =
    1 2 3 4 6
    4 5 6 1 3

>> D = A(1:2, 2:3)
D =
    2 3
    5 6

Exemplo de indexação por vetor:

>> A = [ 1 2 3; 4 5 6;7 8 9]
A =
1 2 3
4 5 6
7 8 9
>> C = [1 3]
C =
1 3
>> B = A(C,C)
B =
1 3
7 9

Acesso a elementos específicos:

>> A = [ 1 2 3; 4 5 6] % constr´oi uma matriz 2 x 3
A =
1 2 3
4 5 6
>> A(2,3) = 0 % modifica o valor do elemento A(2,3)
A =
1 2 3
4 5 0
>> A(3,5) = 1 % coloca o valor 1 no elemento A(3,5)
a =
1 2 3 0 0
4 5 0 0 0
0 0 0 0 1

Note que no último caso o tamanho de A é expandido e preenchido com zeros para que o elemento A(3,5) possa existir.

Para preencher uma coluna toda com certo escalar podemos proceder da seguinte forma:

>> A(:,4) = [3; 3; 3]
A =
1 2 3 3 0
4 5 0 3 0
0 0 0 3 1

Dadas as possibilidades de erros, há uma forma alternativa que envolve expansão escalar:

>> A(:,4) = 3
A =
1 2 3 3 0
4 5 0 3 0
0 0 0 3 1

Submatrizes

A(i, j) retorna a entrada (i, j) da matriz A (escalar = matriz 1 x 1)
A(i,: ) retorna a linha i de A (como vetor linha)
A(:, j) retorna a coluna j de A (como vetor coluna)
A(2 : 4,3 : 7) retorna as linhas de 2 a 4 e as colunas de 3 a 7 (como matriz 3 x 5)
A([2 4],:) retorna linhas 2 e 4 e todas as colunas (como matriz 2 x n )
A(;) retorna uma coluna longa formada pelas colunas de A ( matriz mn x 1)
triu(A) define todas as entradas abaixo da diagonal principal como zero (triangular superior)
tril(A) define todas as entradas acima da diagonal principal como zero (triangular inferior)

Funções de manipulação

fliup(m)

Retorna a matriz com as linhas de elementos de m em ordem inversa.

>> A = [1 2 3;4 5 6;7 8 9]
A =
    1 2 3 
    4 5 6 
    7 8 9

>> F = flipud(A)
F =
    7 8 9
    4 5 6
    1 2 3

fliplr(m)

Retorna a matriz com as colunas de elementos de m em ordem inversa.

>> F = fliplr(A)
F =
    3 2 1
    6 5 4
    9 8 7

rot90(A, k)

Rotaciona o vetor k ∗ 90 graus no sentido anti-horário. Se k estiver ausente, assume k = 1.

>> A= reshape(1:6,2,3)
A =
1 3 5 6 4 2
>> rot90(A,2)
ans =
2 4 6 5 3 1

triu(A)

Produz uma matriz cuja parte triangular superior (incluindo a diagonal principal) é a mesma de A e o restante dos elementos são zeros.

tril(A)

Análoga à anterior, mas triangular inferior.

>> tril(A)
ans =
1 0 0 1 3 5
>> triu(A)
ans =
2 4 0 0 4 6

reshape(m,nl,nc)

Esta função redistribui os elementos de uma matriz m como especificado nos argumentos.

O argumento nl determina o número de linhas de redistribuição e o argumento nc o número de colunas.

>> A = 1:6
A =
1 2 3 4 5 6
>> reshape(A,2,3) >> reshape(A,[2 3])
ans = ans =
1 3 5 1 3 5
2 4 6 2 4 6
>> reshape(A,1,5)
??? Error using ==> reshape
To RESHAPE the number of elements must not change.

Esta função é usada para replicar vetores como especificado nos argumentos.

>> A = reshape(1:4,2,2)
A =
1 3
2 4
>> repmat(A,1,3) % = repmat(A,[1 3]) = [A A A]
ans =
1 3 1 3 1 3
2 4 2 4 2 4
>> repmat(A,2,2) % = repmat(A,2) = [A A; A A]
ans =
1 3 1 3
2 4 2 4
1 3 1 3
2 4 2 4

 

Matriz identidade

o comando eye(arg) retorna uma matriz de ordem m×n com os elementos (i,i) = 1 para i = 1 : min{m, n}. com os demais elementos igual ao escalar 0.

 

Matriz inversa

Dada uma matriz M, conhecemos como matriz inversa de M a matriz M-1 cujo produto M · M-1 é igual à matriz identidade In. Para que uma matriz tenha inversa, ela precisa ser quadrada, e seu determinante tem que ser diferente de 0.

Calculamos determinantes somente de matrizes quadradas, ou seja, matrizes em que a quantidade de colunas e a quantidade de linhas são iguais. Para calcular o determinante de uma matriz, precisamos analisar a ordem dela, ou seja, se ela é 1x1, 2x2, 3x3 e assim sucessivamente. Quanto maior for a ordem mais difícil será encontrar o determinante. No entanto, há métodos importantes como a regra de Sarrus, utilizada para calcular-se determinantes de matrizes 3x3.

Vejamos exemplos de matrizes que são inversas:

Calculando o produto A . B, temos que:

Note que o produto entre A e B gerou a matriz I2. Quando isso acontece, dizemos que B é a matriz inversa de A. 

O comando inv(m) retorna a matriz inversa da matriz m.

 

Y = inv (X) calcula o inverso da matriz quadrada X.
X ^ (- 1) é equivalente a inv (X).
x = A \ b é calculado de forma diferente de x = inv (A) * b e é recomendado para resolver sistemas de equações lineares.
 

 

 

Calcule o inverso de uma matriz 3 por 3.

X = [1 0 2; -1 5 0; 0 3 -9]
X = 3×3

     1     0     2
    -1     5     0
     0     3    -9


Y = inv(X)
Y = 3×3

    0.8824   -0.1176    0.1961
    0.1765    0.1765    0.0392
    0.0588    0.0588   -0.0980

Verifique os resultados. Idealmente, Y * X produz a matriz de identidade. Uma vez que inv realiza a inversão da matriz usando cálculos de ponto flutuante, na prática Y * X é próximo, mas não exatamente igual, ao olho da matriz de identidade (tamanho (X)).

Y*X
ans = 3×3

    1.0000    0.0000   -0.0000
         0    1.0000   -0.0000
         0   -0.0000    1.0000
 
 

View MATLAB Command

 

Examine why solving a linear system by inverting the matrix using inv(A)*b is inferior to solving it directly using the backslash operator, x = A\b.

Create a random matrix A of order 500 that is constructed so that its condition number, cond(A), is 1e10, and its norm, norm(A), is 1. The exact solution x is a random vector of length 500, and the right side is b = A*x. Thus the system of linear equations is badly conditioned, but consistent.

n = 500; 
Q = orth(randn(n,n));
d = logspace(0,-10,n);
A = Q*diag(d)*Q';
x = randn(n,1);
b = A*x;

Solve the linear system A*x = b by inverting the coefficient matrix A. Use tic and toc to get timing information.

tic
y = inv(A)*b; 
t = toc
t = 0.0228

Find the absolute and residual error of the calculation.

err_inv = norm(y-x)
err_inv = 3.7806e-06

res_inv = norm(A*y-b)
res_inv = 4.5557e-07

Now, solve the same linear system using the backslash operator \.

tic
z = A\b;
t1 = toc
t1 = 0.0129

err_bs = norm(z-x)
err_bs = 2.6540e-06

res_bs = norm(A*z-b)
res_bs = 2.5737e-15

The backslash calculation is quicker and has less residual error by several orders of magnitude. The fact that err_inv and err_bs are both on the order of 1e-6 simply reflects the condition number of the matrix.

The behavior of this example is typical. Using A\b instead of inv(A)*b is two to three times faster, and produces residuals on the order of machine accuracy relative to the magnitude of the data.

Matriz Transposta

A matriz transposta da matriz M é a matriz Mt. Trata-se da matriz que vamos obter quando reescrevemos a matriz M trocando de posição as linhas e colunas, transformando a primeira linha de M na primeira coluna de Mt, a segunda linha de M na segunda coluna de Mt, e assim sucessivamente.

Se a matriz M possui m linhas e n colunas, a sua matriz transposta, ou seja, Mt, vai possuir n linhas e m colunas. Existem propriedades específicas para a matriz transposta.

Como é obtida a matriz transposta?

Dada uma matriz Am x n, conhecemos como a matriz transposta de A a matriz Atn x m. Para encontrar a matriz transposta, basta trocar a posição das linhas e colunas da matriz A. O que for a primeira linha da matriz A será a primeira coluna da matriz transposta At, a segunda linha da matriz A será a segunda coluna da matriz At, e assim sucessivamente.

De forma algébrica, seja M = (mij)m x n , a matriz transposta de M é Mt = (mji) n x m.

Exemplo:

Encontre a matriz transposta da matriz:

A matriz M é uma matriz 3x5, então a sua transposta será 5x3. Para encontrar a matriz transposta, faremos com que a primeira linha da matriz M seja a primeira coluna da matriz Mt.

A segunda linha da matriz M será a segunda coluna da matriz transposta:

Por fim, a terceira linha da matriz M se tornará a terceira coluna da matriz Mt:

Matriz simétrica

Com base no conceito de matriz transposta, é possível definir o que é uma matriz simétrica. Uma matriz é conhecida como simétrica quando ela é igual à sua matriz transposta, ou seja, dada a matriz M, M = Mt.

Para que isso aconteça, a matriz precisa ser quadrada, o que significa que, para que a matriz seja simétrica, o número de linhas deve ser igual ao número de colunas.

Exemplo:

Quando analisamos os termos acima da diagonal principal e os termos abaixo da diagonal principal da matriz S, é possível perceber que há termos que são iguais, o que faz com que ela seja conhecida como simétrica exatamente pela simetria da matriz em relação à diagonal principal.

Se encontrarmos a transposta da matriz S, é possível perceber que St é igual a S.

Como S = St, essa matriz é uma simétrica.

 

 

Matriz oposta

Sendo outro caso de matriz especial, a matriz oposta da matriz M é a matriz -M. Conhecemos como matriz oposta de M = (mij) a matriz -M = (-mij). A matriz oposta é composta pelos termos opostos da matriz M.

Determinante

det(A) é odeterminante (se A for uma matriz quadrada)