Agora que temos duas opções de aplicativos para operar MATLAB, Octave Desktop e Octave Online, podemos formalmente iniciar nosso curso.

No curso apresentaremos imagens capturadas com o Octave Desktop, apenas Octave, mas geralmente as instruções e os resultados serão apresentados no próprio texto, sem captura de imagem, como no exemplo abaixo.

>> x = 1
x = 1

Havendo necessidade, apresentaremos imagens de captura.

Ao rodarmos o Octave é apresentada a janela principal - Janela Octave .

Os nomes das janelas, e das GUIs (GUI - Graphical User Interface - Interface Gráfica de Usuário) presentes nas janelas são aqueles apresentados pelo Octave.

Ao ser iniciado, o Octave disponibiliza a guia Janela de Comandos (JC) para digitarmos nossas instruções.

O símbolo de duas-setas ">>" em frente ao cursor na JC chama-se promp , onde é realizada a entrada de nossos comandos ao Octave.

Comando podem ser terminados com ou sem ponto-e-vírgula ";". Não sendo, retornam o resultado para JC; sendo, não retornam.

>> x = 1 % comando terminado sem ";" retorna o resultado para JC
x = 1

>> y = 2; % comando terminado com ";" não retorna o resultado para JC

Comandos podem ser declarados separados por vírgula na mesma linha.

>> y = 2, z = 3 % Comandos antes de vírgula "," retornam o resultado para a JC
y = 2
z = 3

Podemos utilizar as linhas de comando acima para praticar, as copiando e colando na JC, desde depois do símbolo de prompt ">>" até antes do sinal de comentário "%" de final de linha, embora o comentário seja desconsiderado pelo interpretador MATLAB.

E parabéns, nosso curso está iniciado! Formalmente - agora - apresentamos nossos primeiros comandos.

No decorrer do curso simularemos a digitação de comandos na JC com a seguinte caixa:

>>

Já exemplificando, a operação mais básica do MATLAB é o de atribuição de um valor a uma variável.

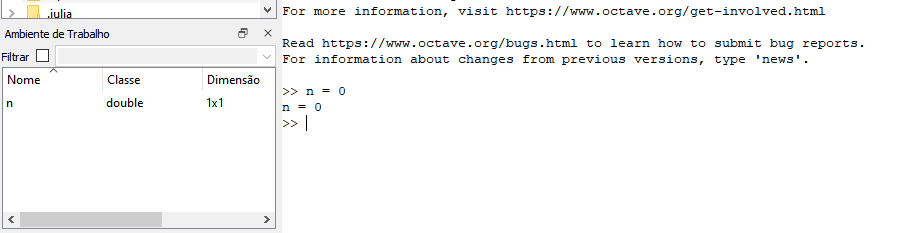
Na JC vamos digitar a instrução n = 0 <ENTER> para criar a variável n com valor igual a zero (escalar).

>> n = 0 % comentário
n = 0

Reparemos que abaixo do comando digitado no prompt ">>" surge o resultado n = 0 da operação da instrução. Porque o comando não foi encerrado com ";", o resutado é apresentado na JC.

A tela do Octave (trecho) aparece como a seguir:

Na instrução anterior o valor 0 foi atribuído à variável n. O símbolo "%" é de comentário e o restante à direita foi desconsiderado na interpretação do comando.

Então lembre-se, a linha iniciada com o símbolo ">>" do prompt em frente indicará uma operação de entrada de comando e sem ">>" indicará que texto se refere ao resultado do comando realizado.

Continuando a apresentação de instruções básicas, uma variável pode receber a soma de valores escalares.

>> n = 2 + 2 % A variável n recebe o resultado de 2 + 2 = 4
n = 4

Na instrução anterior o resultado da soma do escalar 2 mais outro escalar 2 foi atribuído, com valor igual ao escalar 4, à variável n.

Nesta seção são apresentados comandos básicos para criação e manipulação de dados, bem como comandos para criarmos gráficos simples.

Também abordaremos as representações de números, vetores e matrizes à luz do paradigma do MATLAB.

O modo interativo

Logo que o Octave é iniciado nos é apresentada a tela de entrada de comandos.

Digitamos a instrução no prompt >> e pressionamos a tecla <ENTER>.

A tela estará no modo interativo, com o Octave esperando uma instrução ser digitada no prompt - com o cursor posicionado logo após o símbolo ">>" na tela.

Digitamos o comando e a tecla <ENTER>, instruíndo ao Octave sua execução.

Eis alguns exemplos para praticarmos, não nos esquecendo de digitar a tecla <ENTER> ao final da linha. Copie e cole de pois do ">>".

>> x = 1
x = 1
>> y = 2
y = 2
>> z = x + y
z = 3
>> w = x * y
w = 2

Os resultados dos comandos acima são retornados, pois os comandos não são encerrados com ";".

Podemos suprimir a apresentação do texto retornado pela instrução digitada, com a inclusão do ";" (ponto-e-vírgula) ao final da instrução.

>> x = 1;
>> y = 2;
>> z = x + y;
>> w = x * y;

No modo interativo, é extremamente recomendável que o usuário iniciante guarde os comandos (e os resultados) que foram inseridos em uma sessão.

Podemos comandar a MATLAB para que guarde tudo em um arquivo no computador.

Lembrando que estamos nos referindo à linguagem MATLAB, independente de estarmos utilizando Octave Windows ou Octave Online ou mesmo MatLab.

Instruímos o comando diary <nome_do_arquivo.txt>, que irá guardar todos os comandos subsequentes até o final da sessão.

O comando exit no modo interativo encerra o aplicativo.

Ajuda

A ajuda do Octave está em inglês mas é bastante útil, em muitas situações, mesmo para aqueles sem domínio da linguagem, por exemplo para consulta de uma função e seus argumentos.

Para consultar a ajuda de um comando digite:

>> help <nome_do_comando>

Para consultar tópicos do manual:

>> help help
>> help diary
>> help exit

e muito mais.

Outra maneira para conseguirmos ajuda farta e que, por incrível que pareça, funciona melhor ainda, consiste na pesquisa na internet com o mecanismo de busca, tipo Google ou Bing. Algumas vezes você terá texto significativo para o que precisa, por exemplo, uma mensagem de erro retornada de um comando, tipo incompatibilidade de dimensões entre matrizes numa operação matricial. Pesquisando essa mensagem encontraremos, depois de algum tempo e alguma busca, algum artigo com a resposta para o termo pesquisado.

Matrizes, matrizes, matrizes

O paradigma do MATLAB é que todos os elementos são sempre matrizes.

Valores escalares (números inteiros e reais, strings, booleanos) são matrizes unitárias de dimensão de ordem 1, com uma linha e uma coluna (1_x1).

Vetores são matrizes unidimensionais de 1 linha e n colunas (1_xn) ou n linhas e 1 coluna (n_x1), com n > 1.

Matrizes bidimensionais são matrizes multidimensionais (m_xn) com duas ou mais linhas (m > 1 ) e duas ou mais colunas (n > 1 ).

Matrizes m_xn_xp são tridimensionais e a terceira dimensão é chamada de paginação, onde seus elementos são chamados de páginas e são matrizes bidimensionais, afinal a terceira dimensão segue a segunda.

Matrizes com mais de 3 dimensões são polidimensionais e não têm uma classificação específica, e não serão muito utilizadas no curso.

As matrizes podem conter diferentes tipos de valores: escalares (numéricos inteiro ou real, string, lógico, etc) ou matriciais. Matrizes, os valores serão, sempre são.

Matrizes mais complexas serão apresentadas, adiante no curso.

Existe um velho ditado que diz

“Tudo no MATLAB são matrizes.”

Para verificarmos este fato, observamos o comando whos sendo instruído logo após as declarações anteriores de variáveis:

>> x = 1
x = 1

>> y = 2
y = 2

>> z = x + y
z = 3

>> w = x * y
w = 2

>> whos
Name Size Bytes Class
x    1x1  8     double array
y    1x1  8     double array
z    1x1  8     double array
w    1x1  8     double array
Grand total is 4 elements using 32 bytes

A saída do comando whos é o sumário das variáveis armazenadas na memória, descrevendo nomes, dimensões, bytes utilizados e tipo.

Do exemplo acima podemos concluir que todas as variáveis x, y, z e w são matrizes 1_x1 de valores escalares do tipo numérico real (double), consumindo 8 bytes de memória cada uma.

Para sabermos mais sobre o comando whos digitamos:

>> help whos

O que distingue MATLAB das linguagens de programação tradicionais é sua facilidade de trabalhar com vetores e matrizes.

MATLAB tem uma enorme facilidade para trabalhar com matrizes e plotar estas matrizes - dentre muitos recursos - em gráficos em duas ou três dimensões, com variados tipos de apresentação (linhas, barra, malhas, etc).

Vetores e matrizes podem ser facilmente operados - multiplicados, divididos, somados, subtraídos, potenciados, dentre várias operações matemáticas possíveis - seja com escalares ou com outros vetores e matrizes.

Na JC criamos o vetor x com 10 elementos.

>> x = 1:10   % 1:10 é a forma simplificada do MATLAB, sem colchetes, para [1:10]
x = 1 2 3 4 5 6 7 8 9 10

O vetor x foi declarado com 2 argumentos entre colchetes ([) e separados por dois-pontos (:) e criado com 10 elementos com os valores 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.

Declarações de matrizes com ":" podem suprimir os colchetes em situações mais simples de declaração. Aproveitamos o exemplo anterior para mostra r isso.

O primeiro valor é o inicial (do primeiro elemento da sequência da matriz), e o segundo valor é o final (do último elemento da matriz), com variação de 1 a partir do valor inicial até o valor final ser atingido.

Agora criaremos um vetor com os valores dos elementos de y iguais aos das posições correspondentes em x elevados ao quadrado.

>> j = x .^ 2
y = 1, 4, 9, 16, 25, 36, 49, 64, 91, 100

Acima apresentamos nossa primeira operação com matrizes, de exponenciação: retornamos em y uma matriz com as mesmas dimensões de x, contendo os elementos correspondentes aos de x nas posições, com o valor de x em cada posição sendo elevado a 2, usando o operador-eae de potencialização ".^".

Operações com matrizes na matemática teórica têm limites que a MATLAB supera com operações-eae, elemento a elemento.

Veremos mais sobre operadores-eae adiante e, no momento , precisamos saber apenas que a maioria das operações entre matrizes, aritméticas (com operações matemáticas básicas), algébricas (com equações usando letras e números), ou outras, usarão o ponto "." antes do operador aplicado: multiplicação-eae ".*", divisão-eae "./" ou ".\", soma-eae ".+", subtração-eae ".-", potencialização-eae ".^".

Também podemos declarar vetores com "[ ]" e ":" com 3 argumentos: valor inicial, valor final e variação.

>> x = 0 : 0.1 : 1   % equivalente a [ 0 : 0.1 : 1 ]
x = 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

O vetor x foi declarado com 2 argumentos entre colchetes ([) e separados por dois-pontos (:) e criado com 10 elementos com os valores 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.

Declarações de matrizes com ":" podem suprimir os colchetes em situações mais simples de declaração. Aproveitamos o exemplo anterior para mostra r isso.

Criamos o vetor y com os valores dos elementos iguais aos das posições correspondentes em x multiplicados por pi.

>> y = x * pi
y = 0 0.3142 0.6283 0.9425 1.2566 1.5708 1.8850 2.1991 2.5133 2.8274 3.1416

Acima apresentamos a operação com multiplicação de um escalar (da constante pi do MATLAB) com um vetor: retornamos em y um vetor com as mesmas dimensões de x, contendo os elementos nas posições correspondentes de x, com o valor de x em cada posição sendo multiplicado por pi usando o operador escalar de multiplicação "*".

A MATLAB permite a utilização dos operadores escalares "+", "-", "*" e "" entre escalares e matrizes nas operações aritméticas (adição, subtração, multiplicação e divisão).

O vetor y é criado com 10 posições respectivamente preenchidas com os valores 1, 4, 9, 16, 25, 36, 49, 64, 91, 100.

É importante ressaltar que os operadores matemáticos para números escalares e vetores são diferentes.

Para elevar um número escalar ao quadrado usamos ^

>> k = 10
k = 10
>> z = k ^ 2
z = 100

mas para elevar um vetor por um escalar ou por outro vetor ou matriz usamos ".^":

>> k = [1:3]
k = [1,2,3]
>> z = k .^ 2
z = [1,4,9]

Exemplos

Alguns exemplos para praticarmos:

1. Matriz A 4_×3 (4 linhas e 3 colunas), com as linha declaradas separadas por ponto-e-vírgula e as colunas separadas por vírgula.

>> A = [1, 2, 3; 1, 4,7;2, 6, 1; 4, 5,0]
A =
   1   2   3
   1   4   7
   2   6   1
   4   5   0

2. Matriz O 2_×4, com valores iguais a 1.

>> O = ones(2,4)
O =
   1   1   1   1
   1   1   1   1

3. Matriz Z 3_×4, com valores igual a 0 (zero).

>> Z = zeros(3,4)
Z =
   0   0   0   0
   0   0   0   0
   0   0   0   0

4. Matriz E 3_x3, identidade.

>> E = eye(3)
E =
Diagonal Matrix
   1   0   0
   0   1   0
   0   0   1

Uma vez que os exemplos acima foram testados, os comandos abaixo podem ser inseridos (linha a linha, observando que o texto após o caracter % não precisa ser digitado).

>> C = 2*A                                    % multiplicacao por escalar
>> D = [3, 4, 5; 1, 6, 3; 2, 2, 9; -1, 0, 17] % inserindo uma nova matriz
>> F = A + D                                  % adição de matrizes
>> G = A -D                                   % subtração de matrizes
>> T = G'                                     % transposta de matriz
>> M = F * T                                  % multiplicação de matrizes
>> P = inv(M)                                 % inversa de matriz
>> a = det(P)                                 % determinante de matriz

Plotagem de gráficos

Existem duas funções básicas para plotagem de gráficos: fplot e plot.

fplot

A função fplot permite-nos fornecer como primeiro argumento uma função, entre aspas simples ou duplas, e como segundo argumento o intervalo sobre o qual a função será plotada.

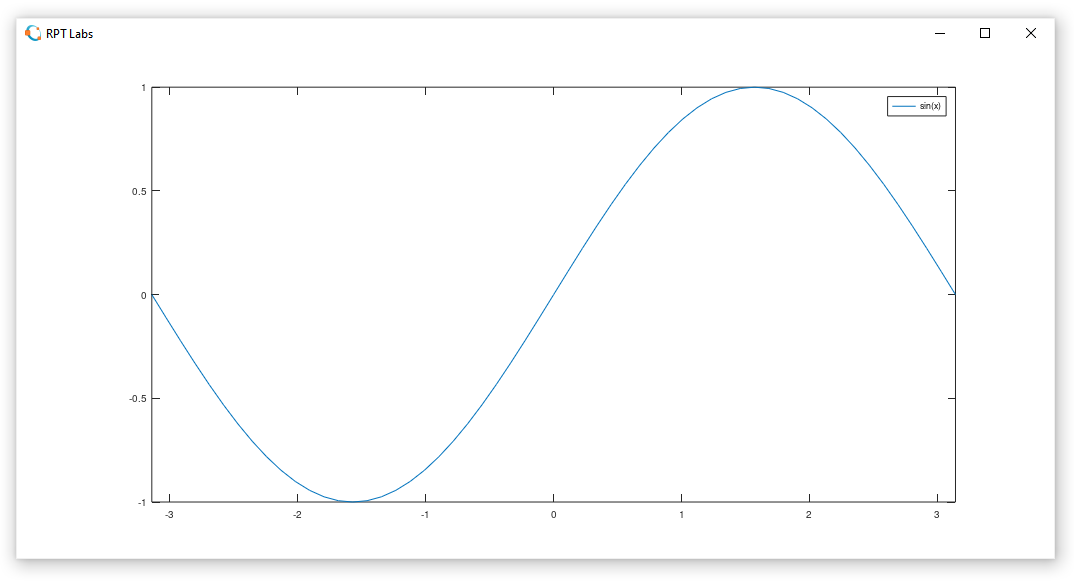
>> fplot('sin(x)',[-pi,pi])

A janela "Figure 1" é aberta com o gráfico plotado da função acima:

>> fplot('cos(x)',[-pi,pi])

A janela "Figure 1" apaga o gráfico atual e apresenta o da função acima.

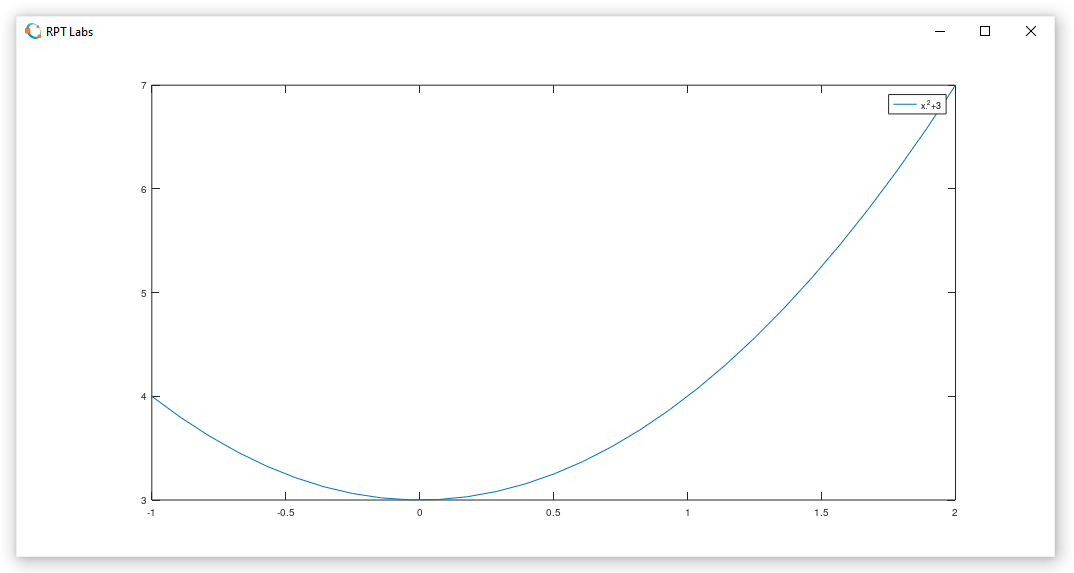
>> fplot('x^2+3',[-1,2])

Novamente a janela "Figure 1" apaga o gráfico atual e apresenta o da função acima, do primeiro grau.

Existem outras opções que podem ser verificadas com help fplot.

plot

Usamos a função plot para produzir gráficos 2D com vetores e matrizes, através de discretização e operações eae, que serão explicadas mais à frente.

Vejamos o exemplo abaixo:

>> x = 1:10
x =    1    2    3    4    5    6    7    8    9   10

A forma mais simples de criamos um vetor simples é atribuindo a uma variável a igualdade "=" das posições inicial e final do vetor separadas por ":", com variação implícita de 1, como no exemplo anterior.

A discretização ocorre quando realizamos uma operação envolvendo uma função (ou um escalar) e um vetor, que chamaremos vetor-operando.

É retornado um vetor com o mesmo número de posições do vetor-operando, com o valor do resultado da operação na posição correspondente.

>> y = x .^ 2
y =    1     4     9    16    25    36    49    64    81   100

o comando a seguir plota o gráfico de x _x y.

>> plot(x,y)

Na janela Figure 1 é a presentado o gráfico dos vetores x e y.

Discretização de funções

Basicamente uma discretização de uma função f(x) qualquer ocorre quando uma sequência de números é gerados a partir de outra sequência de números usando a própria função como a regra para a geração da nova sequência.

A sequência à qual é aplicada a função é chamada de domínio discretizado e a outra sequência de imagem discretizada.

Para que tudo corra bem, no entanto, há a condição de que todos os números do domínio discretizado sejam distintos.

Se existir repetição, ainda vai funcionar para todos os efeitos, mas não teremos mais uma função, teremos outra coisa que estará fora do escopo desta abordagem.

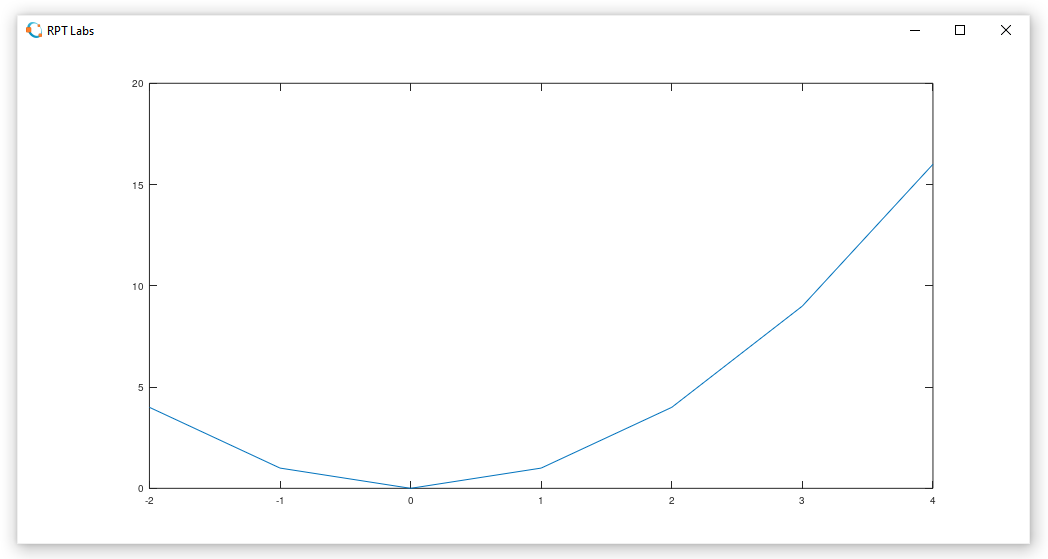
Por exemplo se a função é f(x)= x², podemos considerar a sequência de números

>> xn = [−2,−1,0,1,2,3,4]
xn =  -2  -1   0   1   2   3   4

e quando aplicamos a função f a cada um dos números de xn geramos outra sequência de números :

>> yn = xn.^2
yn =    4    1    0    1    4    9   16

Juntando as duas sequências em pares obtemos uma discretização da função:

[(−2,4),(−1,1),(0,0),(1,1),(2,4),(3,9),(4,16)]

como a realizada pelo comando plot.

>> plot (xn,yn)

produzindo o gráfico

Discretização é a descrição aproximada, por vários pares ordenados (xn,yn), de uma função, onde os valores de xn são todos distintos e, de preferência mas não necessariamente, ordenados de forma crescente.

Podemos notar, portanto, que um vetor (geralmente muito grande) pode representar uma discretização de uma função, quando o domínio - isto é, a sequência de números à qual será aplicada a função - é o conjunto de números naturais.

De outra forma, uma função discretizada deve ser representada por dois vetores com a mesma dimensão (geralmente grande), onde um representa o domínio discretizado e o outro a imagem discretizada.

Operações elemento-a-elemento (eae)

O MATLAB tem a capacidade específica de realizar operações com vetores elemento-a-elemento (“elementwise”), vista a seguir.

Para multiplicar duas matrizes, é necessário que as as dimensões sejam compatíveis, como no exemplo:

A(3×5).B(5×1) = C(3x1)

O leitor pode conferir que o número de colunas da matriz à esquerda (A) é igual ao número de linhas da matriz à direita (B), satisfazendo a condição para a multiplicação entre matrizes. Por outro lado, não é possível realizar a multiplicação de duas matrizes com mesma dimensão m × n, como por exemplo m =5 e n = 3:

A(5×3).B(5×3) = ?? − Impossível !

Outra coisa impossível de se fazer é a divisão de uma matriz por outra, não importando quais sejam as dimensões

A(m×n) = ?? − Impossível !
------
B(p×q)

Na MATLAB usamos o sinal de ponto do lado esquerdo da operação desejada (sem espaço entre os símbolos) com matrizes que possuam as mesmas dimensões, digamos m×n, para realizar as chamadas elemento-a-elemento (eae), incluindo a multiplicação-eae e divisão-eae.

Multiplicação-eae:

>> A = B .* C

Divisão-eae:

>> A = B ./ C

Potenciação-eae:

>> A = B .^ C

Para fixarmos a ideia das operações eae, vamos testar os comandos abaixo:

>> X = [3, 4, 5; 1, 6, 3; 2, 2, 2; -1, 1, 2] % inserindo uma nova matriz
>> Y = [2, 0, 4; 0, 1, 6; 4, 1, 0; -1, 0, 7] % inserindo uma nova matriz
>> M = X .* Y                                % multiplicação eae
>> D = X ./ Y                                % divisão eae
>> A = X .+ Y                                % soma eae
>> S = X .- Y                                % subtração eae
>> P = X .^ Y                                % potenciação eae

2.5.3 Criação de funções mais complexas

Dado essa grande quantidade de ferramentas eae e os conceitos de discretização, é possível unirmos esses dois mundos para criar funções (discretizadas) bem complexas
com MATLAB.

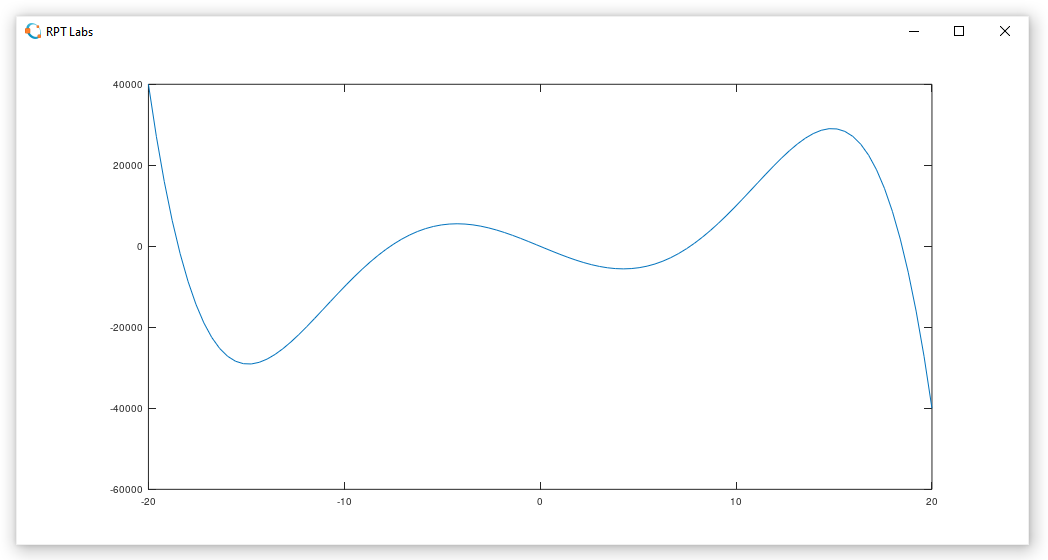
Por exemplo, suponha que desejamos criar uma função polinomial do quinto grau abaixo para examinarmos o seu gráfico.

f(x)= −0.1x5 + 40x3 − 2000x − 5

Como proceder?

Em primeiro lugar definimos o domínio discretizado como o comando linspace, por exemplo.

A função linspace(<A>,<B>,<C>) cria um vetor de <A> até <B> com <C> elementos.

>> x = linspace(-20, 20, 100)
x =
 Columns 1 through 13:
  -20.0000  -19.5960  -19.1919  -18.7879  -18.3838  -17.9798  -17.5758  -17.1717  -16.7677  -16.3636  -15.9596  -15.5556  -15.1515
   ...
   Columns 92 through 100:
   16.7677   17.1717   17.5758   17.9798   18.3838   18.7879   19.1919   19.5960   20.0000

No exemplo anterior x recebe um vetor com 100 elementos, onde o primeiro = −20 e o ultimo´= 20, e os valores intermediários estão igualmente espaçados.

Criamos então vetor com a imagem da função discretizada.

>> y = -0.1 * (x .^ 5) + 40 * (x .^ 3) - 2000 * x - 5
y =
   Columns 1 through 10:
   3.9995e+04   2.7148e+04   1.5991e+04   6.3908e+03  -1.7800e+03  -8.6420e+03  -1.4310e+04  -1.8894e+04  -2.2497e+04  -2.5217e+04
   ...
   Columns 91 through 100:
   2.5207e+04   2.2487e+04   1.8884e+04   1.4300e+04   8.6320e+03   1.7700e+03  -6.4008e+03  -1.6001e+04  -2.7158e+04  -4.0005e+04

Para, finalmente, plotarmos o gráfico da função discretizada.

>> plot(x,y)

cujo resultado pode ser conferido na figura abaixo.

2.6 Operações com escalares, uma pequena exceção

Rigorosamente falando, é impossível somar uma constante (que é uma matriz um por um, lembra?) a uma matriz qualquer de dimensões maiores do que um, afinal de contas as dimensões "não batem". No entanto o MATLAB permite este "abuso" entendendo que se deseja somar a constante a todas as entradas da matriz. Isto funciona para todas as outras operações, tais como subtração, multiplicação e divisão, entre outras. Entretanto, o leitor deve tomar cuidado, pois isso não funciona com a potenciação.

Para verificar esta propriedade, testemos os seguintes exemplos:

>> A =[1,2,1;0,1,2;1,3,0]
A =
   1   2   1
   0   1   2
   1   3   0

>> B =5 + A
B =
   6   7   6
   5   6   7
   6   8   5

>> C = 2 * A
C =
   2   4   2
   0   2   4
   2   6   0

>> D = 0.5 - A
D =
  -0.5000  -1.5000  -0.5000
   0.5000  -0.5000  -1.5000
  -0.5000  -2.5000   0.5000

Primeiros comandos e gráficos