Curvas planas

Comandos abordados: help(), linspace(), plot(), sin(), cos().

A forma paramétrica de uma curva plana Γ pode ser descrita através do seguinte par de funções abaixo:

onde t é um parâmetro real que assume valores em um intervalo [a, b] e f(t) e g(t) são funções quaisquer.

Quando t = a, o ponto ( xa , ya ) = ( f(a) , g(a) ) é o início da curva e quando t = b, o ponto ( xb , yb ) = ( f(b) , g(b) ) é o final da curva.

Para fixarmos esta ideia, examinemos os seguintes exemplos:

Para exibirmos as curvas das funções acima, instruímos os comandos a seguir (o texto após o símbolo % é apenas comentário).

Para curva Γ1:

>> t = linspace(0,10*pi,1001); % gera o domínio discretizado
>> x = t + sin(2*t);           % coordenadas x da curva discretizada
>> y = t + 2*cos(5*t);         % coordenadas y da curva discretizada
>> figure(1);                  % aciona a janela gráfica
>> plot(x,y);                  % desenha a curva

Temos a janela Figura 1:

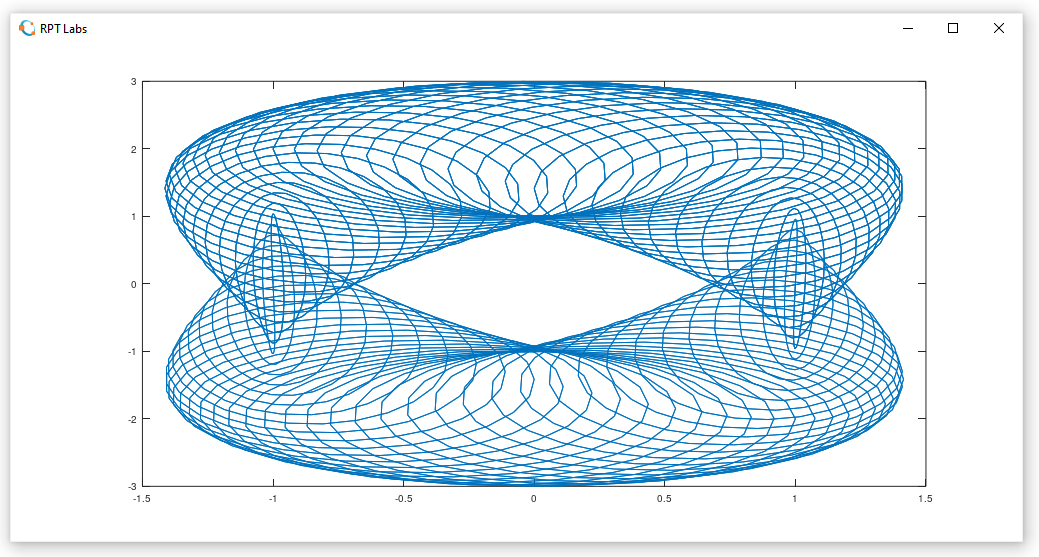
Para curva Γ2:

>> t = linspace(0 , 5*pi , 5001);
>> x = cos(t) - cos(80 * t) .* sin(t);
>> y = 2 * sin(t) - sin(80 * t);
>> figure(2)
>> plot(x,y)

Temos a janela Figura 2:

O leitor mais corajoso certamente trabalhará nos parâmetros das curvas acima para ver o que acontece.