Vimos aula Teoria matemática de operações com vetores que, a partir da multiplicação entre matrizes, é possível compreendermos o que é a matriz identidade, contendo os elemento neutros da multiplicação de matrizes.

O produto de M por M^-1 é igual à matriz identidade, onde a matriz M^-1 inversa da matriz M

Também é possível a multiplicação de uma matriz por um número real — nesse caso, multiplicamos cada um dos elementos da matriz pelo número real.

Para multiplicar duas matrizes, é necessário que as as dimensões sejam compatíveis, como no exemplo:

A(3×5).B(5×1) = C(3x1)

O leitor pode conferir que o número de colunas da matriz à esquerda (A) é igual ao número de linhas da matriz à direita (B), satisfazendo a condição para a multiplicação entre matrizes. Por outro lado, não é possível realizar a multiplicação de duas matrizes com mesma dimensão m × n, como por exemplo m =5 e n = 3:

A(5×3).B(5×3) = ?? − Impossível !

Outra coisa impossível de se fazer é a divisão de uma matriz por outra, não importando quais sejam as dimensões

A(m×n) = ?? − Impossível !
------
B(p×q)

Esta operação causa graves problemas de saúde em professores de matemática quando os alunos insistem em realizá-la.

Contudo, no MATLAB, existem as operações elemento-a-elemento (eae), incluindo a multiplicação-eae e divisão-eae, para operação entre matrizes com dimensões compatíveis.

 

Operações elemento a elemento

Operação	Resultado
Adição	A + c = [a1 + c . . . an + c]
Subtração	A − c = [a1 − c . . . an − c]
Multiplicação	A ∗ c = [a1 ∗ c . . . an ∗ c]
Divisão	A/c = c\A = [a1/c . . . an/c]
Exponenciação	A.ˆc = [ac1 . . . acn] c. ˆA = [ca1 . . . can ]

Não há problemas de o vetor A ser bi-dimensional

>> c = 2; A = 1:2:10;
>> A+c
ans = 3 5 7 9 11
>> A-c
ans = -1 1 3 5 7
>> A*c
ans = 2 6 10 14 18
>> A/c % mesmo que c\A
ans = 0.5000 1.5000 2.5000 3.5000 4.5000
>> A.ˆc
ans = 1 9 25 49 81
>> c.ˆA
ans = 2 8 32 128 512

  Sejam A = [a1 . . . an] e B = [b1 . . . bn] vetores.

Operação	Resultado
Adição	A + B = [a1 + b1 . . . an + bn]
Subtração	A − B = [a1 − b1 . . . an − bn]
Multiplicação	A. ∗ B = [a1 ∗ b1 . . . an ∗ bn]
Divisão esq.	A./B = [a1/b1 . . . an/bn
Divisão dir.	B.\A = [a1/b1 . . . an/bn]
Exponenciação	A.ˆB = [ab11 . . . abnn ]

 Exemplo - vetor e vetor

>> A = 1:5;
>> B=5:-1:1;
>> A+B
ans = 6 6 6 6 6
>> A-B
ans = -4 -2 0 2 4
>> A.*B
ans = 5 8 9 8 5
>> A./B
ans = 0.2000 0.5000 1.0000 2.0000 5.0000
>> A.\B
ans = 5.0000 2.0000 1.0000 0.5000 0.2000
>> A.ˆB
ans = 1 16 27 16 5

As operações elemento a elemento podem ser usadas em expressões matemáticas, desde que respeitadas as dimensões dos vetores envolvidos.

A precedência dos operadores é a tradicional.

>> A = [1 2 3; 4 5 6];
>> B = [7 8 9; 10 11 12];
>> 2 * A - 1
ans = 1 3 5 7 9 11
>> 2 * A - B
ans = -5 -4 -3 -2 -1 0
>> A.ˆ(B - 1)
ans = 1 128 6561 262144 9765625 362797056

 

 

Operações eae

O MATLAB tem a capacidade específica de realização de operações eae (elemento-a-elemento, elementwise) com matrizes.

Os operadores eae do MATLAB têm o sinal de ponto "." do lado esquerdo da operação desejada (sem espaço entre os símbolos).

Multiplicação-eae:

>> A = B .* C

Divisão-eae:

>> A = B ./ C

Potenciação-eae:

>> A = B .^ C

Para fixarmos a ideia das operações eae, vamos testar os comandos abaixo:

>> X = [3, 4, 5; 1, 6, 3; 2, 2, 2; -1, 1, 2] % inserindo uma nova matriz
>> Y = [2, 0, 4; 0, 1, 6; 4, 1, 0; -1, 0, 7] % inserindo uma nova matriz
>> M = X .* Y                                % multiplicação eae
>> D = X ./ Y                                % divisão eae
>> A = X .+ Y                                % soma eae
>> S = X .- Y                                % subtração eae
>> P = X .^ Y                                % potenciação eae

Operações eae mais complexas

Dado essa grande quantidade de ferramentas eae e os conceitos de discretização, é possível unirmos esses dois mundos para criar funções (discretizadas) bem complexas
com MATLAB.

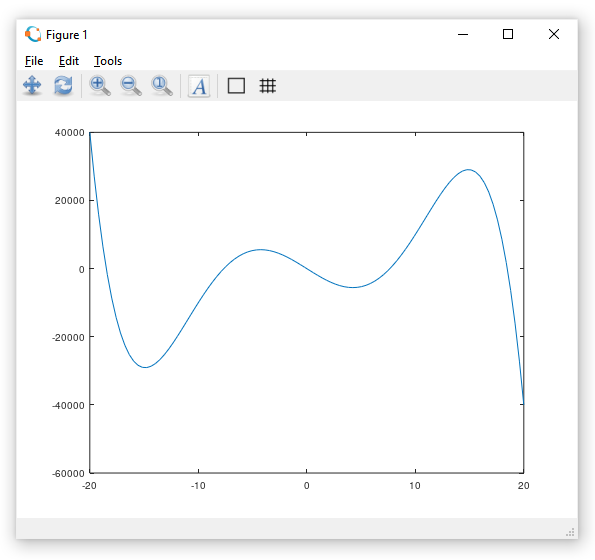
Por exemplo, suponha que desejamos criar uma função polinomial do quinto grau

f(x)= −0.1x⁵ + 40x³ − 2000x − 5

para examinarmos o seu gráfico. Como proceder?

Em primeiro lugar devemos definir o domínio discretizado como o comando linspace:

 

>> x = linspace(-20, 20, 100)
x =
 Columns 1 through 13:
  -20.0000  -19.5960  -19.1919  -18.7879  -18.3838  -17.9798  -17.5758  -17.1717  -16.7677  -16.3636  -15.9596  -15.5556  -15.1515
   ...
   Columns 92 through 100:
   16.7677   17.1717   17.5758   17.9798   18.3838   18.7879   19.1919   19.5960   20.0000

O vetor é criado com 100 elementos, onde o primeiro = −20 e o ultimo´= 20, e os intermediários estão igualmente espaçados.

Depois deve-se criar o vetor que vai representar a imagem da função discretizada:

>> y = -0.1 * (x .^ 5) + 40 * (x .^ 3) - 2000 * x - 5
y =
   Columns 1 through 10:
   3.9995e+04   2.7148e+04   1.5991e+04   6.3908e+03  -1.7800e+03  -8.6420e+03  -1.4310e+04  -1.8894e+04  -2.2497e+04  -2.5217e+04
   ...
   Columns 91 through 100:
   2.5207e+04   2.2487e+04   1.8884e+04   1.4300e+04   8.6320e+03   1.7700e+03  -6.4008e+03  -1.6001e+04  -2.7158e+04  -4.0005e+04

Para, finalmente, plotar o gráfico da função discretizada, utilizamos:

>> plot(x,y)

cujo resultado pode ser conferido na figura abaixo.

2.6 Operações com escalares, uma pequena exceção

Rigorosamente falando, é impossível somar uma constante (que é uma matriz um por um, lembra?) a uma matriz qualquer de dimensões maiores do que um, afinal de contas as dimensões "não batem". No entanto o MATLAB permite este  "abuso" entendendo que se deseja somar a constante a todas as entradas da matriz. Isto funciona para todas as outras operações, tais como subtração, multiplicação e divisão, entre outras. Entretanto, o leitor deve tomar cuidado, pois isso não funciona com a potenciação.

Para verificar esta propriedade, testemos os seguintes exemplos:

>> A =[1,2,1;0,1,2;1,3,0]
A =
   1   2   1
   0   1   2
   1   3   0

>> B =5 + A
B =
   6   7   6
   5   6   7
   6   8   5

>> C = 2 * A
C =
   2   4   2
   0   2   4
   2   6   0

>> D = 0.5 - A
D =
  -0.5000  -1.5000  -0.5000
   0.5000  -0.5000  -1.5000
  -0.5000  -2.5000   0.5000