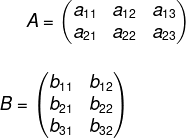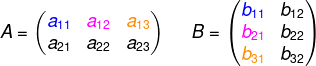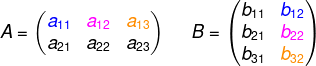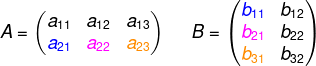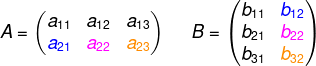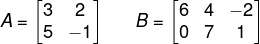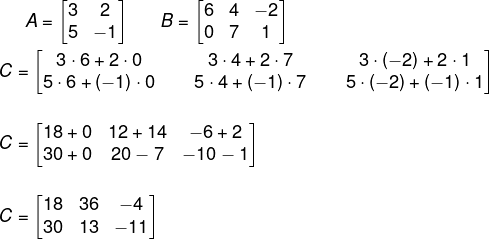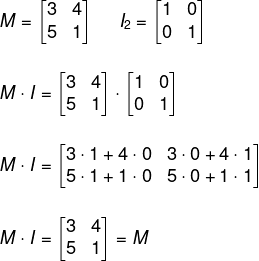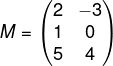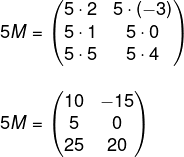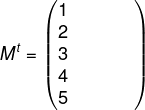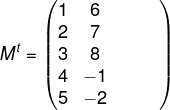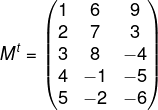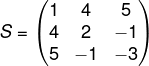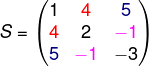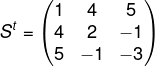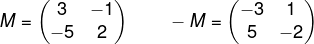Na teoria conceitual das matrizes as operações são restritas, por exemplo a multiplicação de matrizes é feita por meio de um algoritmo que exige bastante atenção.
Para que exista o produto entre a matriz A e a matriz B, é necessário que o número de colunas da primeira matriz, no caso A, seja igual ao número de linhas da segunda matriz, no caso B.
Para multiplicarmos duas matrizes, primeiramente é necessitamos verificar a condição de existência.
Para que o produto exista, o número de colunas da primeira matriz tem que ser igual ao número de linhas da segunda matriz.
Além disso, o resultado da multiplicação é uma matriz que possui o mesmo número de linhas da primeira matriz e o mesmo número de colunas da segunda matriz.
Por exemplo, o produto AB entre as matrizes A3x2 e B2x5 existe, pois o número de colunas de A (2 colunas) é igual ao número de linhas de B (2 linhas), e o resultado é uma matriz AB3x5.
Já produto entre as matrizes C3x5 e a matriz D2x5 não existe, pois C possui 3 linhas e D possui 5 colunas.
Operações com matrizes
Multiplicação de matrizes
Para realizarmos a multiplicação de matrizes, necessitamos seguir algumas passos.
Faremos um exemplo da multiplicação de uma matriz algébrica A2x3 pela matriz B3x2
Sabemos que o produto existe, pois a matriz A possui 3 colunas, e a matriz B possui 3 linhas.
Chamaremos de C o resultado da multiplicação A·B.
Além disso, também sabemos que o resultado é uma matriz C2x2, pois a matriz A tem 2 linhas, e a matriz B, 2 colunas.
Para calcular o produto entre a matriz A2x3 e a matriz B3x2, primeiramente encontramos cada um dos termos da matriz C2x2:
Para encontrar os termos, vamos relacionar sempre as linhas da matriz A com as colunas da matriz B:
c11 → 1ª linha de A e 1ª coluna de B
c12 → 1ª linha de A e 2ª coluna de B
c21 → 2ª linha de A e 1ª coluna de B
c22 → 2ª linha de A e 2ª coluna de B
Calculamos cada um dos termos realizando a multiplicação entre os termos da linha de A e os termos da coluna de B.
Somamos agora os produtos, começando por c11, operando os elementos da 1ª linha de A e da 1ª coluna de B.
Calculamos c12 operando os elementos da 1ª linha de A e da 2ª coluna de B.
Calculamos c21 operando os elementos da 2ª linha de A e da 1ª coluna de B.
Calculamos c22 operando os elementos da 2ª linha de A e da 2ª coluna de B.
Sendo assim, a matriz C é formada pelos termos:
Exemplo:
Vamos calcular a multiplicação entre as matrizes A e B.
Sabemos que, em A2x2 e B2x3, o número de colunas da primeira é igual ao número de linhas da segunda, então o produto existe. Assim, faremos C = A· B e sabemos que C2x3. Multiplicando, temos que:
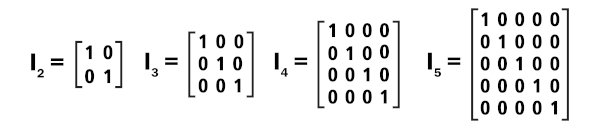
Matriz identidade
Na multiplicação entre matrizes, existem alguns casos especiais, como a matriz identidade, que é o elemento neutro da multiplicação entre matrizes. A matriz identidade é uma matriz quadrada, ou seja, o número de linhas é sempre igual ao número de colunas. Além disso, nela somente os termos da diagonal são iguais a 1, e os demais termos são todos iguais a zero. Quando multiplicamos uma matriz M pela matriz identidade In, temos que:
M · In = M
Matrizes identidade de ordem 2 até a ordem 5:
Exemplo:
Matriz inversa
Dada uma matriz M, conhecemos como matriz inversa de M a matriz M-1 cujo produto M · M-1 é igual à matriz identidade In. Para que uma matriz tenha inversa, ela precisa ser quadrada, e seu determinante tem que ser diferente de 0.
Calculamos determinantes somente de matrizes quadradas, ou seja, matrizes em que a quantidade de colunas e a quantidade de linhas são iguais. Para calcular o determinante de uma matriz, precisamos analisar a ordem dela, ou seja, se ela é 1x1, 2x2, 3x3 e assim sucessivamente. Quanto maior for a ordem mais difícil será encontrar o determinante. No entanto, há métodos importantes como a regra de Sarrus, utilizada para calcular-se determinantes de matrizes 3x3.
Vejamos exemplos de matrizes que são inversas:
Calculando o produto A . B, temos que:
Note que o produto entre A e B gerou a matriz I2. Quando isso acontece, dizemos que B é a matriz inversa de A.
O comando inv(A) retorna a matriz inversa de A na MATLAB.
Matriz Transposta
A matriz transposta da matriz M é a matriz M' posicionando os elementos das linhas em colunas e vice-versa.
A primeira linha de M torna-se a primeira coluna de M', a segunda linha de M torna-se a segunda coluna de M', e assim sucessivamente.
Se a matriz M possui m linhas e n colunas, a sua matriz M' transposta, possuirá n linhas e m colunas.
Existem propriedades específicas para a matriz transposta.
Exemplo:
Sendo a matriz M uma matriz de ordem 3x5 sua transposta será uma matriz de ordem 5x3.
Para encontrar a matriz transposta M', faremos com que sua primeira linha assuma os valores dos elementos da primeira coluna da matriz M.
A segunda linha da matriz M será a segunda coluna da matriz transposta:
Por fim, a terceira linha da matriz M se tornará a terceira coluna da matriz Mt:
Matriz simétrica
Com base no conceito de matriz transposta, é possível definir o que é uma matriz simétrica. Uma matriz é conhecida como simétrica quando ela é igual à sua matriz transposta, ou seja, dada a matriz M, M = Mt.
Para que isso aconteça, a matriz precisa ser quadrada, o que significa que, para que a matriz seja simétrica, o número de linhas deve ser igual ao número de colunas.
Exemplo:
Quando analisamos os termos acima da diagonal principal e os termos abaixo da diagonal principal da matriz S, é possível perceber que há termos que são iguais, o que faz com que ela seja conhecida como simétrica exatamente pela simetria da matriz em relação à diagonal principal.
Se encontrarmos a transposta da matriz S, é possível perceber que St é igual a S.
Como S = St, essa matriz é uma simétrica.
Matriz oposta
Sendo outro caso de matriz especial, a matriz oposta da matriz M é a matriz -M. Conhecemos como matriz oposta de M = (mij) a matriz -M = (-mij). A matriz oposta é composta pelos termos opostos da matriz M.
Determinante
det(A) é odeterminante (se A for uma matriz quadrada)
